Содержание
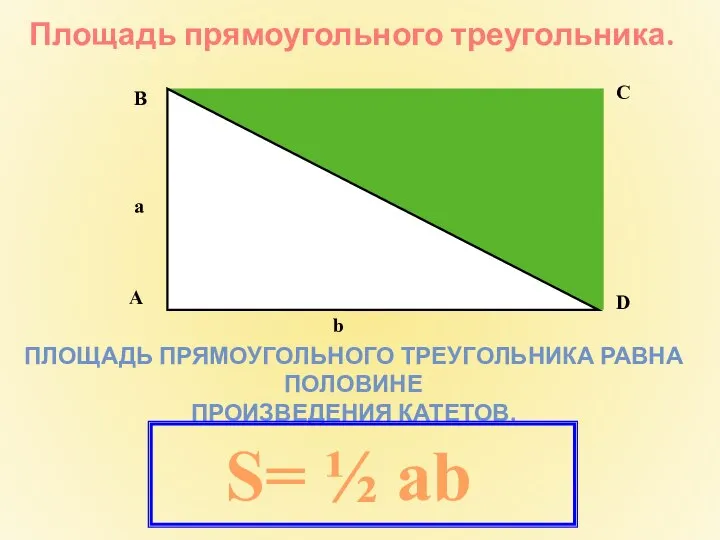
- 2. Площадь прямоугольного треугольника. ПЛОЩАДЬ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА РАВНА ПОЛОВИНЕ ПРОИЗВЕДЕНИЯ КАТЕТОВ. А С В D b a
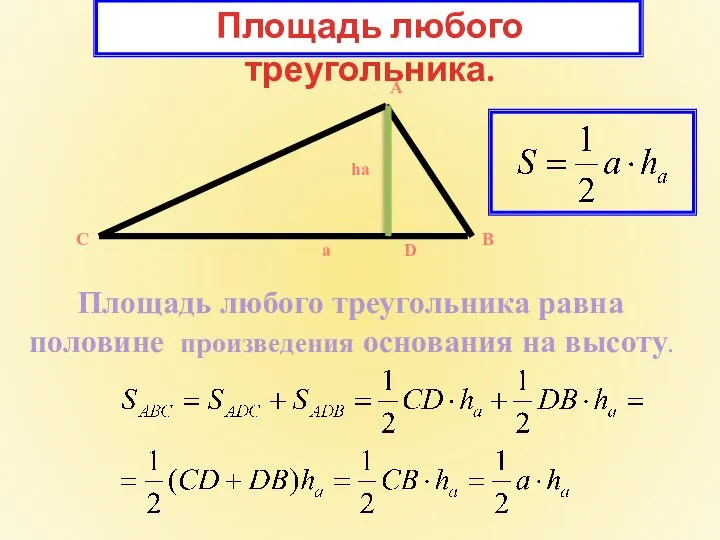
- 3. Площадь любого треугольника. А a B C D ha Площадь любого треугольника равна половине произведения основания
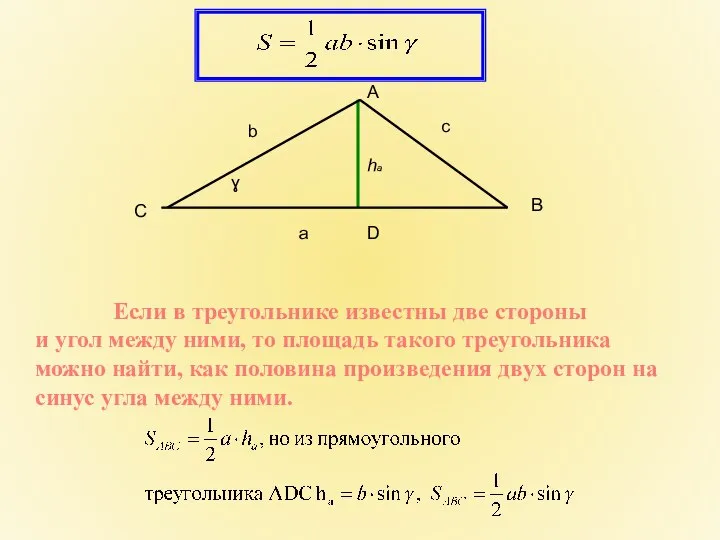
- 4. Если в треугольнике известны две стороны и угол между ними, то площадь такого треугольника можно найти,
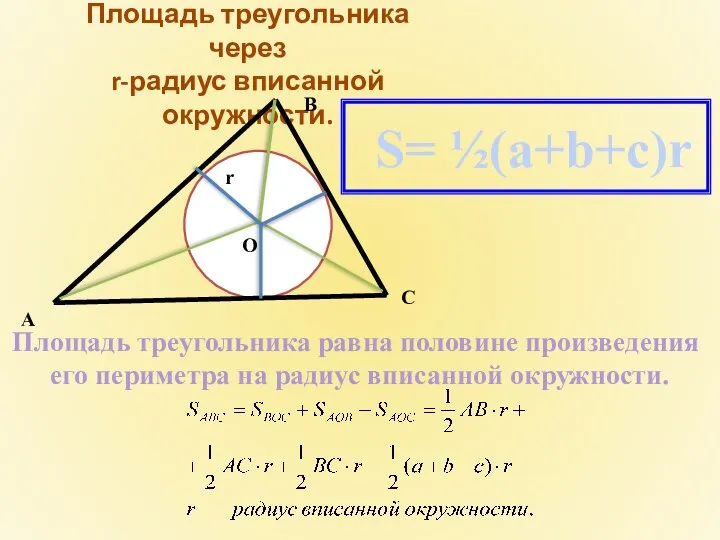
- 5. Площадь треугольника через r-радиус вписанной окружности. Площадь треугольника равна половине произведения его периметра на радиус вписанной
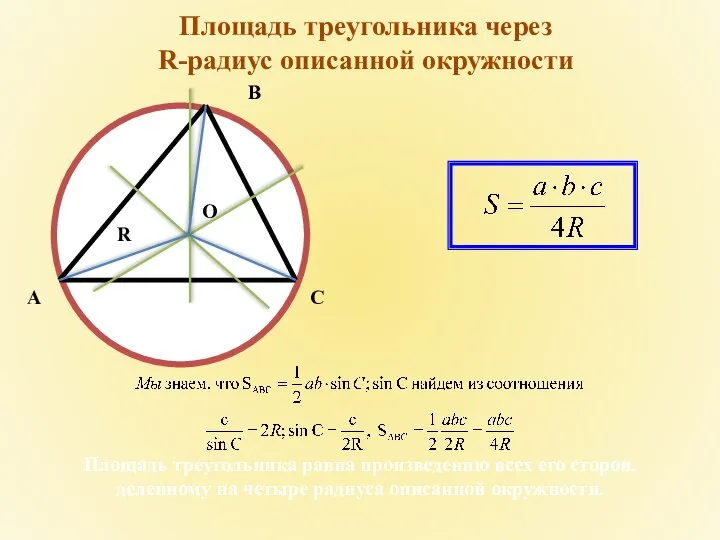
- 6. Площадь треугольника через R-радиус описанной окружности Площадь треугольника равна произведению всех его сторон, деленному на четыре
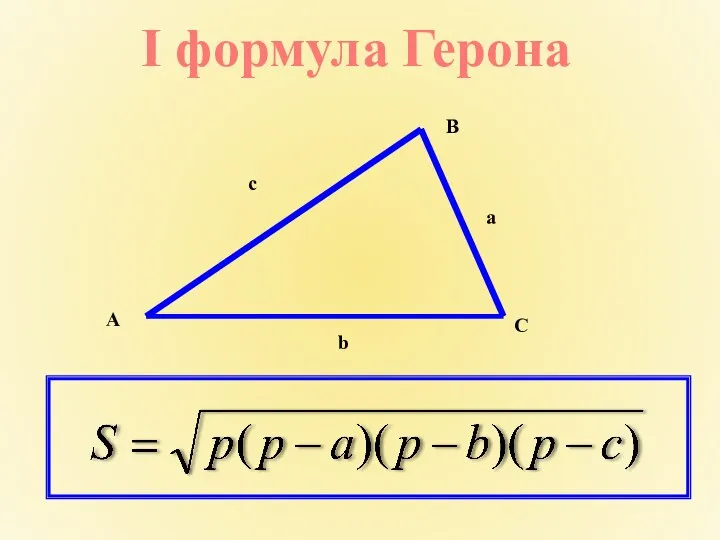
- 7. I формула Герона B C A b с a
- 8. ГЕРОН АЛЕКСАНДРИЙСКИЙ (Heronus Alexandrinus) Герон Александрийский – греческий учёный, работавший в Александрии,(даты рождения и смерти неизвестны,
- 9. II формула Герона B C A
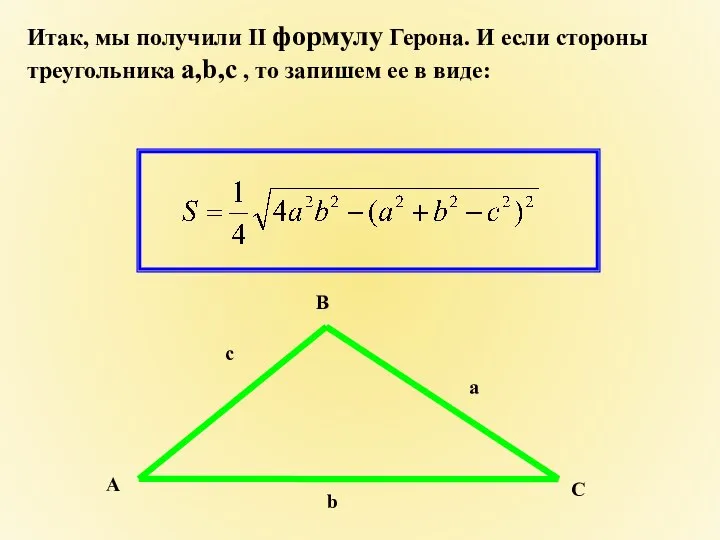
- 10. Итак, мы получили II формулу Герона. И если стороны треугольника а,b,с , то запишем ее в
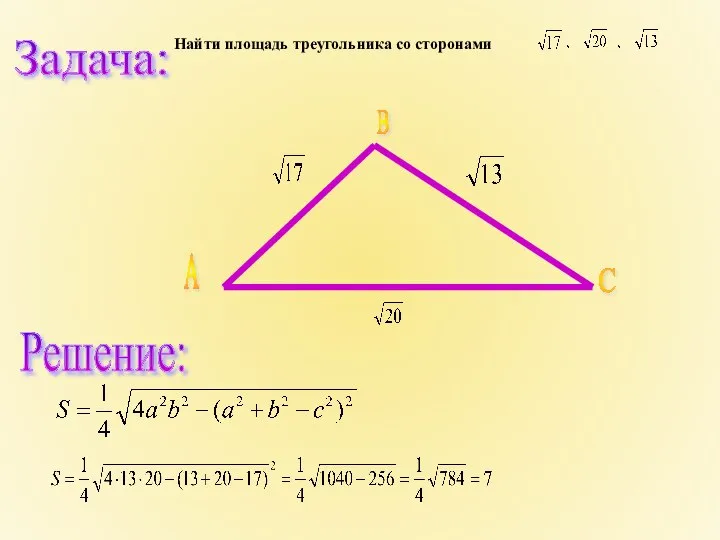
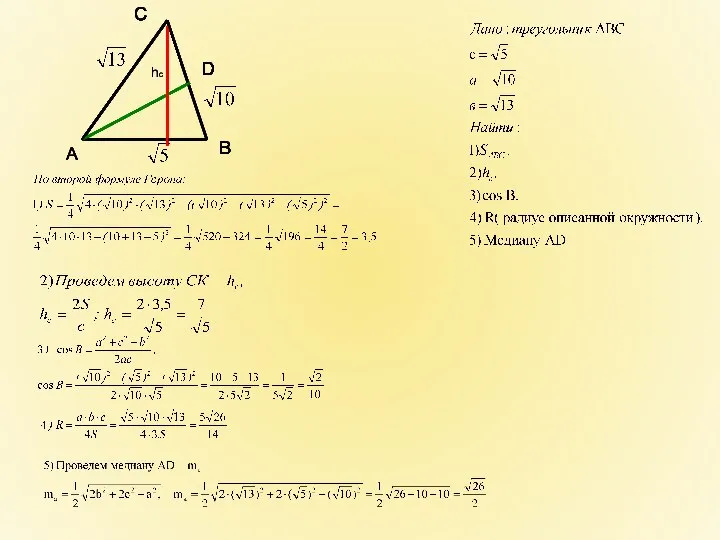
- 11. Найти площадь треугольника со сторонами Решение: Задача: А В С
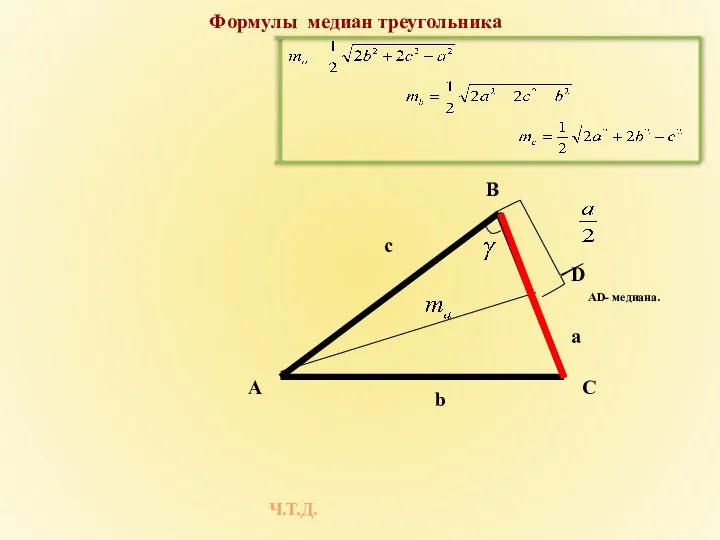
- 12. Формулы медиан треугольника AD- медиана. Ч.Т.Д. C А B b a c D
- 13. C C C C C C C C C C C C D B A hc
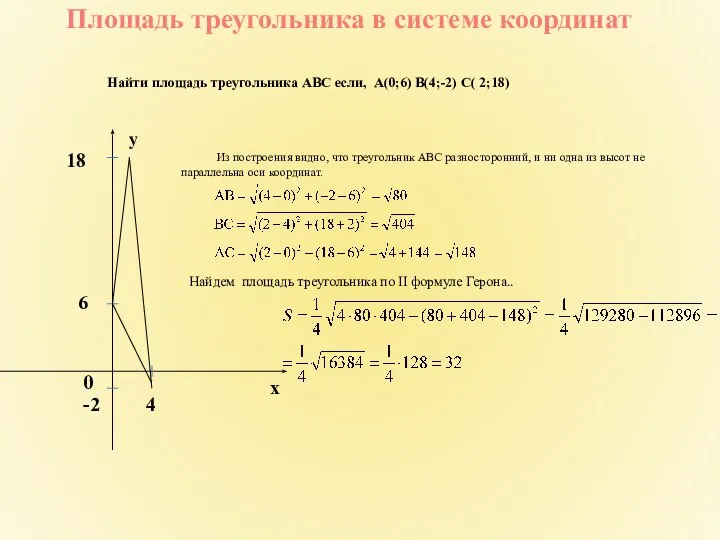
- 14. Площадь треугольника в системе координат Найти площадь треугольника АВС если, А(0;6) B(4;-2) C( 2;18) Из построения
- 15. Семь формул для нахождения площадей различных треугольников.
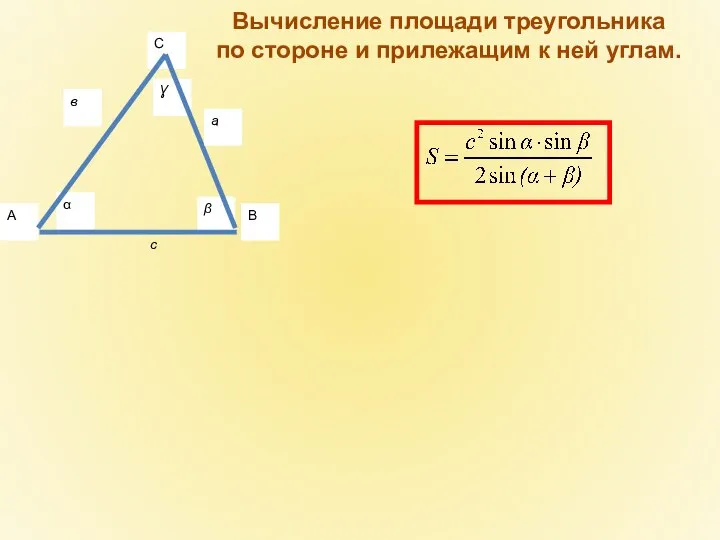
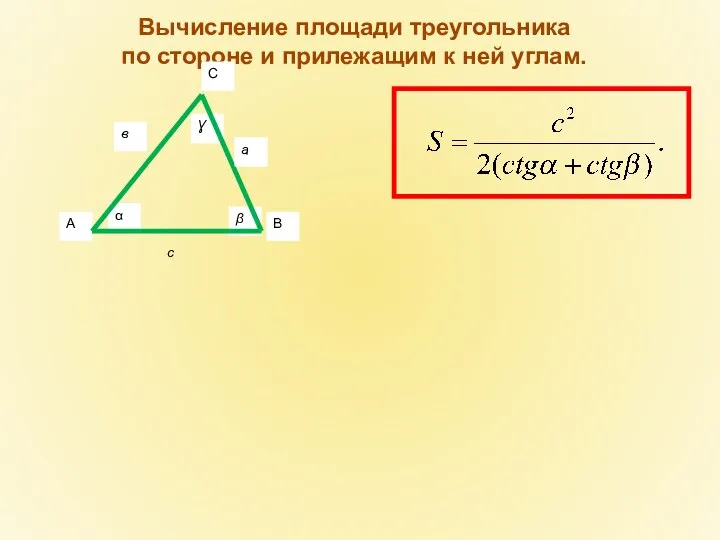
- 16. с Вычисление площади треугольника по стороне и прилежащим к ней углам.
- 17. Вычисление площади треугольника по стороне и прилежащим к ней углам.
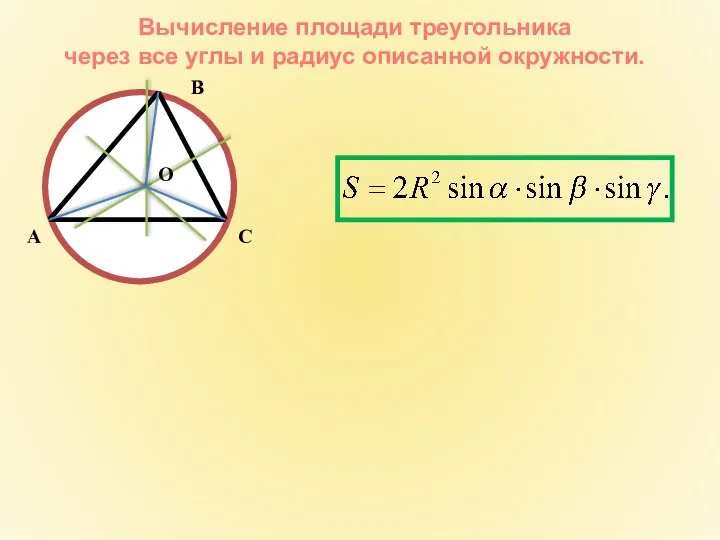
- 18. Вычисление площади треугольника через все углы и радиус описанной окружности.
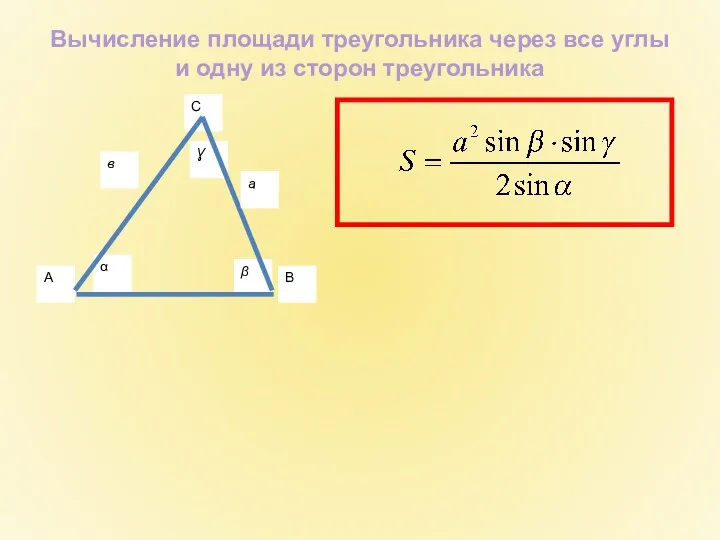
- 19. Вычисление площади треугольника через все углы и одну из сторон треугольника
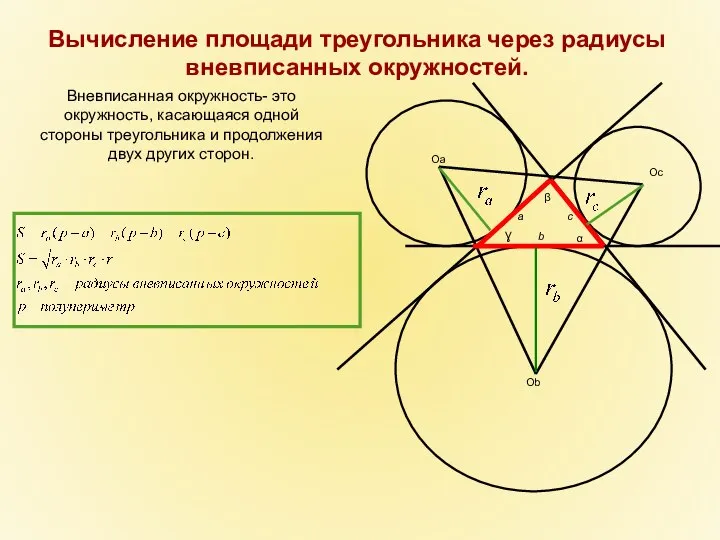
- 20. Oa Ob Oc β a Ɣ b c α Вневписанная окружность- это окружность, касающаяся одной стороны
- 22. Скачать презентацию



 Созвездия. Сималтиниус Раунд Тэйбл
Созвездия. Сималтиниус Раунд Тэйбл Суммы чисел
Суммы чисел Сфера
Сфера Методология нелинейного функционально - факторного моделирования природных и техногенных явлений
Методология нелинейного функционально - факторного моделирования природных и техногенных явлений Працюємо з відсотками і вирішуємо завдання
Працюємо з відсотками і вирішуємо завдання Многогранники
Многогранники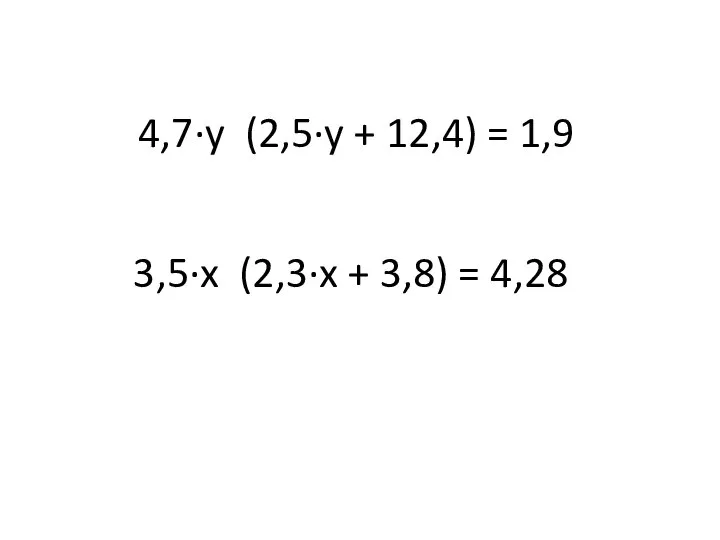 Учение о десятичных дробях
Учение о десятичных дробях Презентация на тему Арифметические действия с числами
Презентация на тему Арифметические действия с числами  Отрезок. Длина отрезка
Отрезок. Длина отрезка Построение симметричных фигур
Построение симметричных фигур Презентация на тему Упрощение выражений 5 класс
Презентация на тему Упрощение выражений 5 класс  Уравнения высших степеней
Уравнения высших степеней Подготовка к ЕГЭ по математике
Подготовка к ЕГЭ по математике Перпендикуляр, наклонная, проекция наклонной
Перпендикуляр, наклонная, проекция наклонной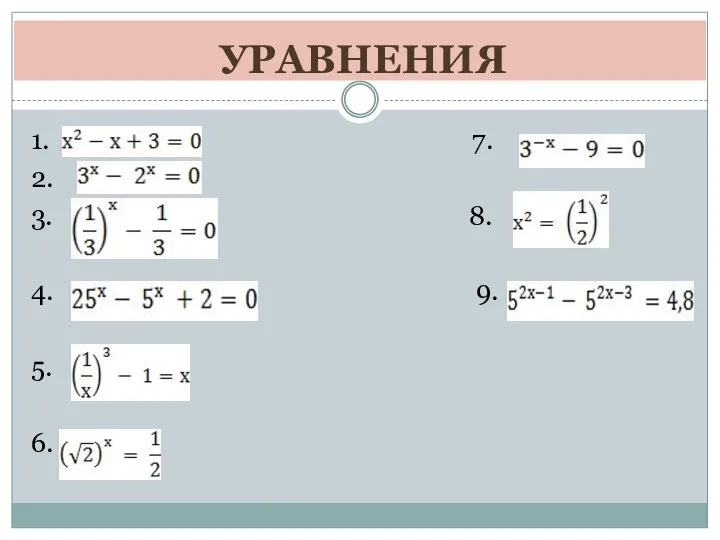 Решение показателей уравнений
Решение показателей уравнений Длина окружности и лощадь круга. Правила
Длина окружности и лощадь круга. Правила Правильные многогранники
Правильные многогранники Математика и статистика для анализа данных
Математика и статистика для анализа данных Спрощення виразів. Підготовка до ЗНО
Спрощення виразів. Підготовка до ЗНО Основные понятия математического анализа. Принятые обозначения числовых множеств
Основные понятия математического анализа. Принятые обозначения числовых множеств Проценты. Три задачи
Проценты. Три задачи Метод интервалов. Общий метод интервалов
Метод интервалов. Общий метод интервалов Засели числовые домики
Засели числовые домики Тема_5_2022
Тема_5_2022 Задачи и примеры по математике
Задачи и примеры по математике Метр. (2класс)
Метр. (2класс) Основные понятия комбинаторики. Факториал. Вычисление факториала
Основные понятия комбинаторики. Факториал. Вычисление факториала Преобразование логарифмических выражений
Преобразование логарифмических выражений