Содержание
- 2. Литература 1. Демидович, Б.П. Дифференциальные уравнения: учеб. пособие 3– е изд., стер. / Б.П. Демидович, В.П.
- 3. §1. Основные понятия теории ОДУ. Df1. Дифференциальное уравнение (ДУ) – равенство, содержащее неизвестную функцию под знаком
- 4. Df2. Порядком дифференциального уравнения называется максимальный порядок производной, который встречается в уравнении.
- 5. где Df3. Общим решением дифференциального уравнения ого порядка называется его решение, выраженное явно относительно неизвестной функции
- 6. Пример 1. (*) Решение.
- 7. Частным решением дифференциального уравнения называется решение, получаемое из общего решения подстановкой вместо произвольных постоянных определённых чисел.
- 8. Общим интегралом дифференциального уравнения является его общее решение, выраженное в виде неявной функции. Общий интеграл дифференциального
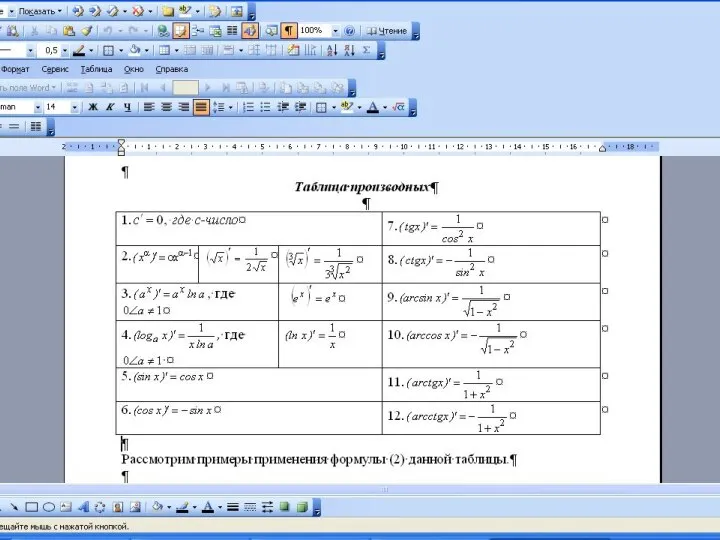
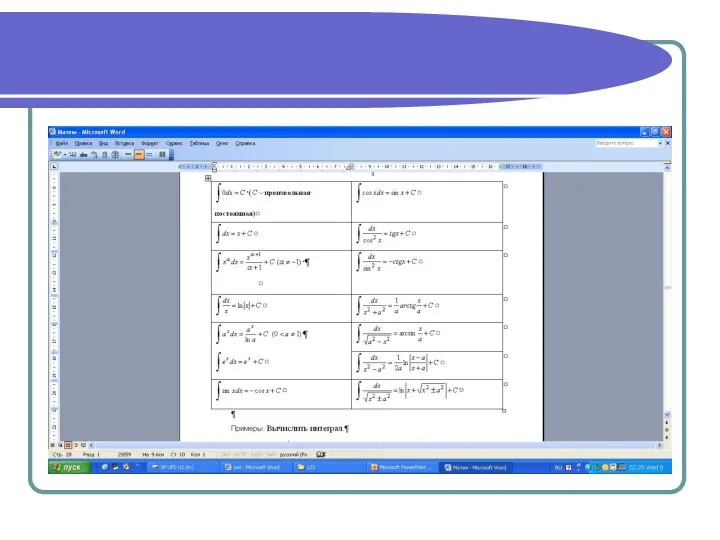
- 10. Таблица производных
- 13. Скачать презентацию








 Деление на 2
Деление на 2 Презентация к уроку математики 6 класса учителя математики НОУ СОШ «Азъ Буки Веди» Ивахненко Натальи Геннадьевны
Презентация к уроку математики 6 класса учителя математики НОУ СОШ «Азъ Буки Веди» Ивахненко Натальи Геннадьевны Множества натуральных чисел
Множества натуральных чисел Арифметическая прогрессия
Арифметическая прогрессия Системы нелинейных неравенств с двумя переменными
Системы нелинейных неравенств с двумя переменными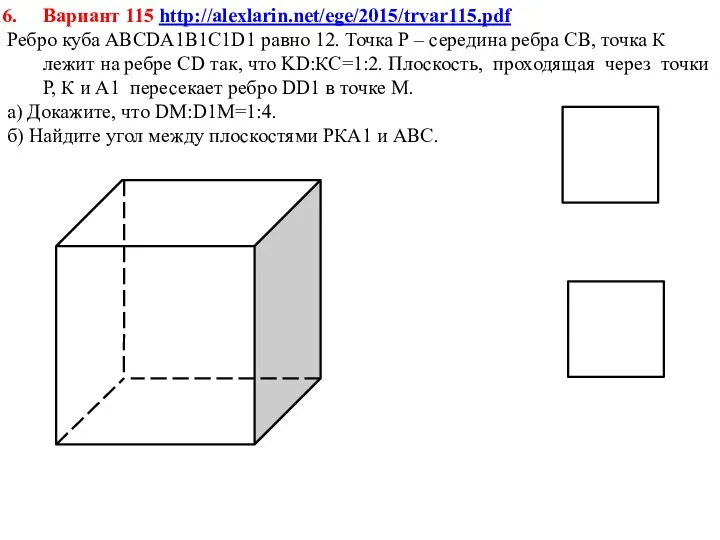 Решение задач. Куб, параллелепипед, призма
Решение задач. Куб, параллелепипед, призма Веселый счет (Счет в прямом и обратном порядке в пределах 10)
Веселый счет (Счет в прямом и обратном порядке в пределах 10) Многогранники. Призма
Многогранники. Призма Теория вероятностей. Случайные события
Теория вероятностей. Случайные события Задачи на движение в противоположных направлениях
Задачи на движение в противоположных направлениях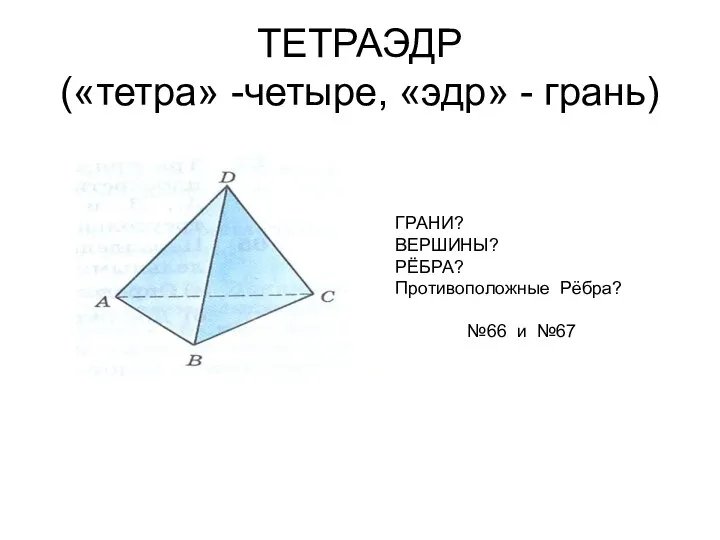 Тетраэдр (тетра -четыре, эдр - грань)
Тетраэдр (тетра -четыре, эдр - грань) Võrratused Heldena Taperson
Võrratused Heldena Taperson Задания по математике (5 класс, часть 6)
Задания по математике (5 класс, часть 6) Степенная функция
Степенная функция Симметрия. 9 класс
Симметрия. 9 класс Удивительные свойства натуральных чисел
Удивительные свойства натуральных чисел Формальные логические теории
Формальные логические теории Решение задач с помощью системы уравнений. 7 класс
Решение задач с помощью системы уравнений. 7 класс Ломаная. Многоугольники
Ломаная. Многоугольники Официальная статистика как условие устойчивого развития сельского хозяйства
Официальная статистика как условие устойчивого развития сельского хозяйства Презентация на тему Объем призмы
Презентация на тему Объем призмы  комбинаторика 1 лекция-1
комбинаторика 1 лекция-1 Уравнение
Уравнение Умножение и деления дробей
Умножение и деления дробей Сравнение дробей
Сравнение дробей Решение задач на дроби. 6 класс
Решение задач на дроби. 6 класс Призмы. Виды призм
Призмы. Виды призм Эволюция. Прогрессия
Эволюция. Прогрессия