1_теория множеств

Дискретная математика (ДМ), или дискретный анализ - область математики, которая занимается исследованиями структур и задач на конечных множествах. Поэтому в качестве синонима иногда используется термин "конечная математика".

Определение
Одним из фундаментальных, неопределяемых математических понятий является понятие множества.
Множество можно представить себе как соединение, совокупность, собрание некоторых предметов, объединенных по какому-либо признаку:
множество учащихся класса,
множество букв алфавита,
множество натуральных чисел,
множество точек на прямой,
множество книг на полке и т.д..

Определение
Предметы, из которых состоит множество, называются его элементами
например, буква К – элемент множества букв русского алфавита.
Для названия множества иногда используют какое-либо одно слово, выступающее в роли синонима слова «множество» (зрители, стая, семья, фрукты).

Обозначают множества заглавными буквами латинского алфавита или символически с помощью фигурных скобок, в которых указываются его элементы.
Сами элементы некоторого множества будем обозначать малыми латинскими буквами, если они не имеют специальных обозначений:
А; {а, b, c}; {∗,s,h,g}; N={1,2,3,4,5,6,7,8, …}.

Принадлежность предмета некоторому множеству обозначают с помощью символа ∈ (в противном случае используется символ ∉).
Запись а ∈А означает, что а есть элемент множества А.
Аналогично имеем: Δ∈{Δ,ο}.
Запись 4∉{1,2,3} означает, что 4 не принадлежит множеству {1,2,3}.

Основными способами задания множества являются:
1) перечисление всех его элементов: А={а1, а2, …, аn};
2) описание (указание характеристического свойства его элементов). Этот способ требует указания такого признака, который имеется у всех элементов данного множества и не свойственен элементам, не входящим в данное множество.

Например, характеристическим свойством натуральных чисел является возможность их использования при счете каких-либо предметов.
Говоря о множестве четных чисел, мы указываем характеристическое свойство его элементов: М={х∈∈ N | х׃2}, т.е. каждое число, принадлежащее этому множеству, делится на два.

Определение 3
Множества, состоящие из одних и тех же элементов (одинаковыми). Пишут А=В.
Определение 4
Множество, которое не содержит ни одного элемента, называется пустым и обозначается символом ∅.

Слово «много» и математический термин «множество» имеют различный смысл.
Множество может состоять из небольшого количества элементов.
Будем обозначать количество элементов в некотором множестве А через m(А).
Например, если А={а, b, c}, то m(А)=3. Если N – множество всех натуральных чисел, то m(N) = ∞.

Подмножество. Основные числовые множества
Определение 1.
Множество В, состоящее из некоторых элементов данного множества А (и только из них), называется подмножеством (частью) этого множества.
Иначе, если любой элемент множества В принадлежит также множеству А, то множество В называется подмножеством множества А.
Это записывается так: В⊂ А или А⊃В. Говорят, что «В – подмножество А» или «В содержится в А» или «А содержит В».
Заметим, что m(В) ≤m(А).

Если в множестве В найдется хотя бы один элемент, не принадлежащий множеству А, то В не является подмножеством множества А: В⊄А.
Например, отрезок [а, b] не является подмножеством полуинтервала (а, b], т.к. а∈[а, b], но а∉(а, b].

Из опр. 1 следует, что любое множество является подмножеством самого себя, т.е. справедливо утверждение А⊂А.
Полагают также, что пустое множество является подмножеством любого множества.
Пустое множество не содержит ни одного элемента, а значит в нем нет элемента, не принадлежащего любому другому множеству.

Знак ⊂ называется знаком включения.
Отметим основные свойства отношения включения между множествами:
1) ∅⊂А для любого множества А;
2) А⊂А для любого множества А (рефлексивность);
3) из того, что В⊂А не следует А⊂В (не симметричность);
4) если А⊂В и В⊂А, то А=В (антисимметричность);
5) если А⊂В и В⊂С, то А⊂С (транзитивность).

Основные числовые множества:
N={1,2,3,4,…} – множество натуральных чисел;
Z={…,-4,-3,-2,-1,0,1,2,3,4,…} – множество целых чисел (содержит все натуральные числа и числа, им противоположные), N⊂Z;
Q={x ׀х = p/q , где p∈Z, q∈N} – множество рациональных чисел (состоит из чисел, допускающих представление в виде дроби), N⊂Z⊂Q;
R=(-∞;+∞) – множество действительных чисел, Q⊂R (кроме всех рациональных чисел, содержит иррациональные числа.

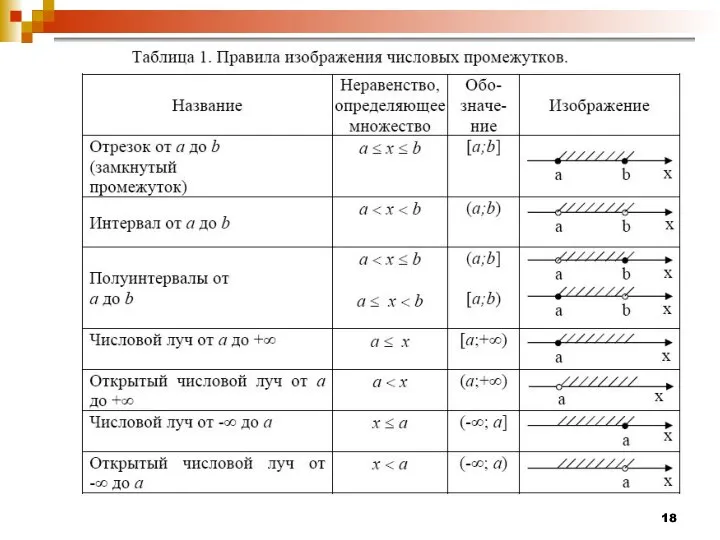
Действительные числа изображаются точками координатной прямой (числовой оси).
Координатная прямая – это всякая прямая (обычно горизонтальная), на которой указаны положительное направление, начало отсчета и единичный отрезок.

Операции над множествами
Два множества могут иметь одинаковые элементы,
из всех элементов двух множеств можно составить одно новое множество,
также можно рассмотреть отдельно элементы одного множества, которых во втором множестве нет.

Например, А – множество наклеек (марок), которые есть у Пети, В – множество наклеек, которые собрал Вася.
Можно выделить множество наклеек, которые есть у обоих ребят;
коллекцию различных наклеек, собранных ими вместе;
множество наклеек Пети, которых нет у Васи.
Таким образом, мы проделали операции пересечения, объединения и разности двух множеств.

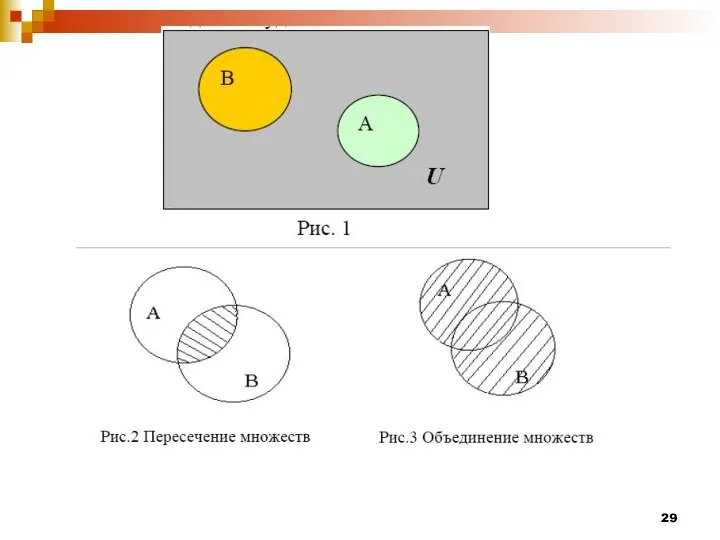
Определение
Пересечением множеств А и В называется множество С, состоящее из всех тех и только тех элементов, которые принадлежат каждому из данных множеств: С={х ׀ х∈А и х∈В}. Обозначается А∩В.

Определение
Объединением множеств А и В называется множество С, которое состоит из всех элементов данных множеств А и В и только из них: С={х׀ х∈А или х∈В}.
Обозначается, А∪В.

Если множества А и В не содержат одинаковых элементов, т.е. не пересекаются (А∩В=∅), то m(А∪В) = m(A) + m(B) (1).
В противном случае, когда множества имеют m(А∩В) одинаковых элементов, следует пользоваться более общей формулой:
m(А∪В) = m(A) + m(B) - m(А∩В) (2).

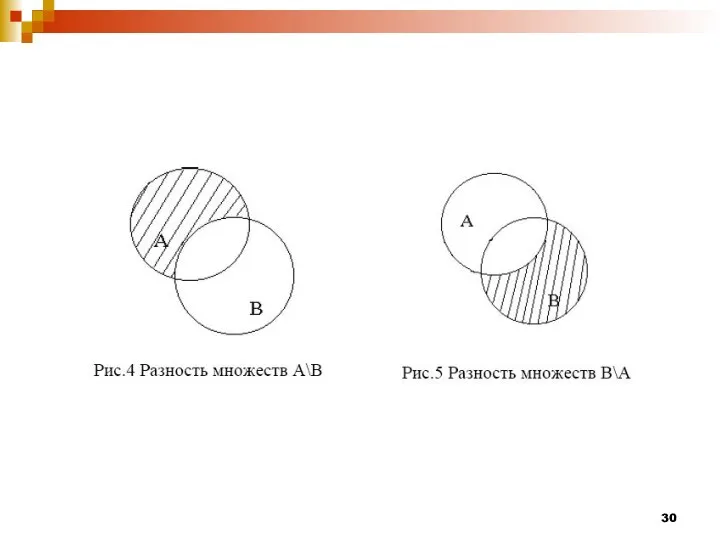
Определение
Разностью множеств А и В называется множество С, состоящее из всех элементов множества А, не принадлежащих множеству В: С={х ׀ х∈А и х∉В}.
Обозначается, А\В.
В случае, когда В является подмножеством А, т.е. В⊂А, разность А\В называется дополнением множества В до множества А (или относительно множества А).

Определение
Универсальным множеством называется множество, подмножества которого (и только они) в данный момент рассматриваются.
Обозначают U.
При работе с числовыми множествами в качестве основного (универсального) множества будем считать множество R действительных чисел.

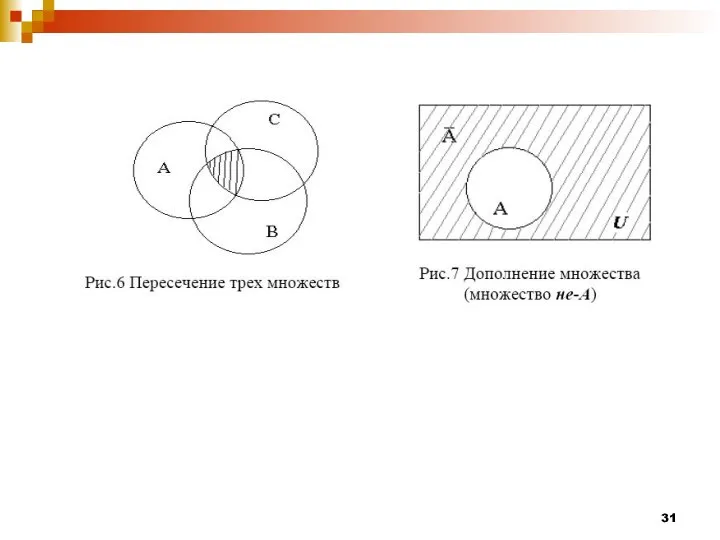
Определение
Дополнением множества А называется разность U\А..
Обозначается, А’ и читается «не А» .
Иначе, дополнением множества А называется множество А’, состоящее из всех элементов, не принадлежащих множеству А.

Диаграммы Эйлера-Венна
Для наглядного представления множеств и результатов операций над ними удобно пользоваться диаграммами Эйлера-Венна (кругами Эйлера).
При этом множества изображаются на плоскости в виде замкнутых кругов, а универсальное множество в виде прямоугольника.
Элементы множества – точки внутри соответствующего круга.

Формула для подсчета числа элементов в объединении трех множеств:
m (А∪В∪С) = m (А) + m (В) + m (С) - m (А∩В) – m (А∩С) – m (В∩С) + m (А∩В∩С)

Примеры
Пример 1. Записать множество всех натуральных делителей числа 15 и найти число его элементов.
Решение: А={1, 3, 5}, m (А)=3.

Пример 2
Даны множества А={2, 3, 5, 8, 13, 15}, В={1, 3, 4, 8,16}, С={12, 13, 15, 16}, D={0, 1, 20}.
Найти А∪В, С∪D, В∩С, А∩D,А\С, D\В, А∪В∪С, А∩В∩С, В∪D∩С, А∩С\D.
Решение:
Учтем, что сначала должна выполняться операция пересечения множеств, а затем объединение или разность.
Получим
А∪В={1, 2, 3, 4, 5, 8, 13, 15, 16},
С∪D={0, 1, 12, 13, 15, 16, 20},
В∩С={16}, А∩D=∅, А\С={2, 3, 5, 8}, D\В={0, 20},
А∪В∪С={1, 2, 3,4, 5, 8, 12, 13, 15, 16},
А∩В∩С=∅, В∪D∩С={1, 3, 4, 8, 16}, А∩С\D={13, 15}

Пример 3.
Экзамен по математике сдавали 250 абитуриентов, оценку ниже пяти получили 180 человек, а выдержали этот экзамен 210 абитуриентов. Сколько человек получили оценки 3 и 4?
Решение: Пусть А – множество абитуриентов, выдержавших экзамен, В – множество абитуриентов, получивших оценку ниже 5, по условию m (A)=210, m (В)=180, m (A∪B)=250. Абитуриенты, получившие оценки 3 и 4, образуют множество А∩В.
Из формулы (2) находим m (A∩B) = m (A) + m (В) - m (A∪B) = 210 + 180 – 250 = 140.

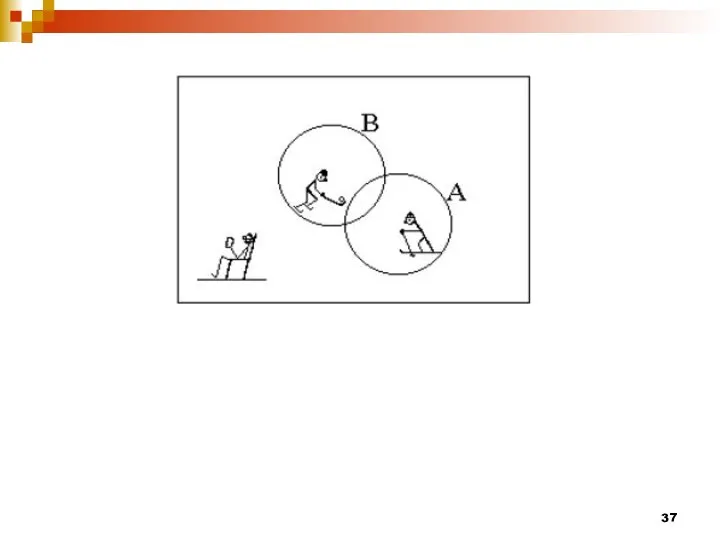
Пример 4.
В школе 1400 учеников.
Из них 1250 умеют кататься на лыжах, 952 – на коньках.
Не умеют кататься 60 учащихся.
Сколько учащихся умеют кататься и на коньках и на лыжах?
Решение: Множество учеников школы будем считать основным множеством U, А и В – соответственно множества учеников, умеющих кататься на лыжах и на коньках .

Учащиеся, не умеющие кататься ни на лыжах, ни на коньках, составляют множество А’∩В’= (А∪B)’
m (А∪B) = m(U) - m (А∪B)’=1340.
m (А∩B) = m (А) + m (В) - m (А∪B) = 862