числа, основание которого остается прежним, а показатели степеней складываются bm∙bn=b(m+n).
При делении степеней с одинаковыми основаниями получают степень числа, основание которого остается прежним, а показатели степеней вычитаются, причем из показателя делимого вычитается показатель делителя
bm:bn=b(m-n).
При возведении степени в степень получается степень числа, основание которого остается прежним, а показатели перемножаются
(bm)n=b(mn)
При возведении в степень произведения чисел в эту степень возводится каждый множитель.
(abc)m=am∙bm∙cm






 Учимся считать. Интерактивный тренажёр
Учимся считать. Интерактивный тренажёр Виды углов.Измерение углов
Виды углов.Измерение углов Презентация на тему Математика вокруг нас. Математика в строительстве
Презентация на тему Математика вокруг нас. Математика в строительстве  Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства
Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства Признаки равенства треугольников
Признаки равенства треугольников Решение уравнений (часть 2)
Решение уравнений (часть 2) Матрицы
Матрицы L(q(x), h, H) шекаралық есептің меншікті мәндері және A(A) характеристикалық функцияның нөлдері
L(q(x), h, H) шекаралық есептің меншікті мәндері және A(A) характеристикалық функцияның нөлдері Функция y = x2 и её график
Функция y = x2 и её график Метод наименьших квадратов оценки параметров функциональной зависимости
Метод наименьших квадратов оценки параметров функциональной зависимости Задачи на готовых чертежах. Ромб
Задачи на готовых чертежах. Ромб Справочный материал. 9 класс
Справочный материал. 9 класс Аналитическая геометрия. Уравнения прямой
Аналитическая геометрия. Уравнения прямой Первый признак подобия треугольников
Первый признак подобия треугольников Презентация на тему Перпендикулярные прямые (7 класс)
Презентация на тему Перпендикулярные прямые (7 класс)  Разработка программы для нахождения корней уравнения методом половинного деления или другим методом
Разработка программы для нахождения корней уравнения методом половинного деления или другим методом Многогранники в природе
Многогранники в природе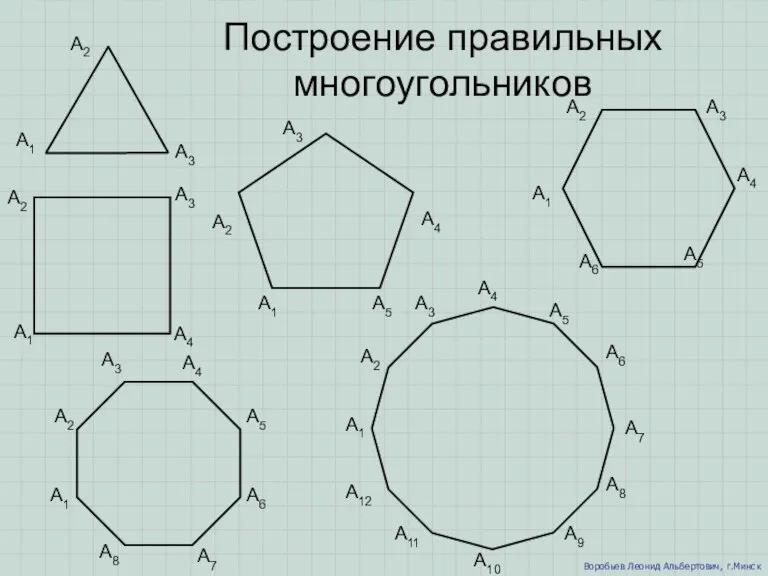 Построение правильных многоугольников
Построение правильных многоугольников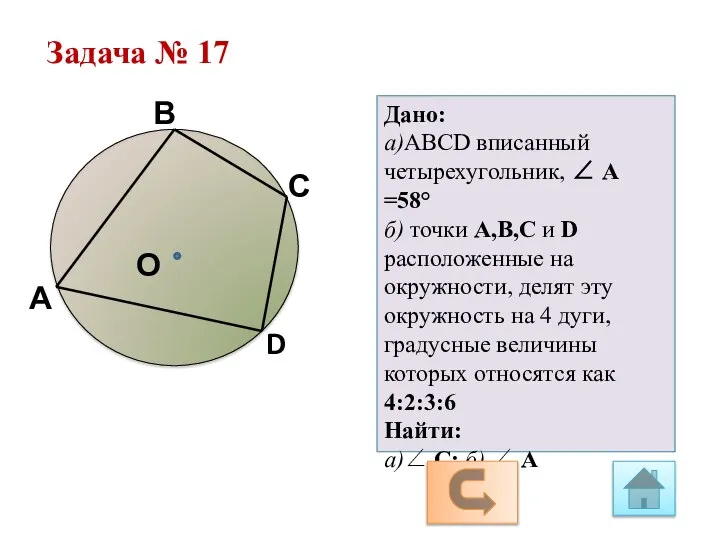 Геометрия 9 класс. Задачи
Геометрия 9 класс. Задачи Основы алгебры логики
Основы алгебры логики Понятие первообразной. Правила нахождения первообразных. Решение примеров на нахождение первообразных
Понятие первообразной. Правила нахождения первообразных. Решение примеров на нахождение первообразных Конструктор (4)
Конструктор (4) Реши примеры
Реши примеры Презентация на тему Парабола
Презентация на тему Парабола  Квадрат и куб. 4 класс
Квадрат и куб. 4 класс Презентация на тему Состав числа 5
Презентация на тему Состав числа 5  Решение задач
Решение задач Обобщение по теме Четырехугольники
Обобщение по теме Четырехугольники