Приемы быстрого счёта в математике

ЦЕЛЬ РАБОТЫ
Изучить методы и приемы быстрого счета и показать возможность их использования для улучшения качества вычислений и для саморазвития

ЗАДАЧИ
Найти и освоить приёмы умножения двузначных и трехзначных чисел
Найти и освоить приемы возведения в квадрат
Найти и освоить извлечение квадратного корня из четырехзначного, пятизначного чисел
Найти и освоить приемы деления чисел

АКТУАЛЬНОСТЬ РАБОТЫ
Эта работа поможет, применяя простые правила и способы быстро выполнять счет и экономить время, выходить из трудностей на ЕГЭ, т.к. там не предусмотрено справочных таблиц

«ПРИЁМЫ УМНОЖЕНИЕ»
1) Это умножение с одинаковым первым множителем
M*P=(M+c)*10a+bc Примеры:
27*24=(27+4)*20+28=648
47*48=(47+8)*40+56=55*40+56=2256

«ПРИЁМЫ УМНОЖЕНИЯ»
2) Это Метод Трахтенберга

«ПРИЁМЫ УМНОЖЕНИЯ»

«ПРИЁМЫ УМНОЖЕНИЯ»
3) Распределительный закон умножения
(a + b)c = ac + bc
(a – b)c = ac – bc
Вычислим 93×34
Запишу число 93 = 100 – 10 + 3 и выполню умножение, раскрыв скобки с помощью распределительного закона:
(100 – 10 + 3) × 34 = 100 × 34 – 10 × 34 + 3 × 34 = 3400 – 340 +102 = 3162

«ПРИЕМЫ УМНОЖЕНИЯ»
4) Умножение на 15
342*15=?
Применим распределительный закон: 342*15=342*(10+5)=(342*10)+(342*5)
(342*5) – это половина от (342*10), => 3420+1710 (Половина 342*10) =5130
128*15=?
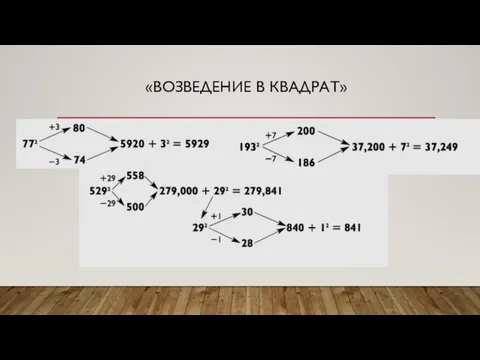
128*15=128*(10+5)=(128*10)+(128*5)=1280+640=1920

«ВОЗВЕДЕНИЕ В КВАДРАТ»
1) Это по формулам
Примеры:

«ВОЗВЕДЕНИЕ В КВАДРАТ»
2)

«ИЗВЛЕЧЕНИЕ КВАДРАТНОГО КОРНЯ»
1) Это четырехзначные числа
√2 809 = 53
3 7
25 < 28< 36
Теперь я должен узнать какое это число: 53 или 57? Буду пользоваться формулой возведения в квадрат
53^2 = (50+3)^2 = 50*(50+6) + 9 =2500+300+9 =
= 2809
Ответ: 53
Зная квадраты однозначных чисел, можно легко вычислить квадратный корень

ИЗВЛЕЧЕНИЕ КВАДРАТНОГО КОРНЯ
2) Это пятизначные числа
√54289=233
1) √54289
2) √5’42’89
√5’42’89 -4
1
4) √5’42’89
-4
- 142
129
13
3
3
5) √5’42’89
-4
-142
129
46 - 1389
1389
0
Ответ: 233
3
3
3
3
*
*
*
3)

«ИЗВЛЕЧЕНИЕ КВАДРАТНОГО КОРНЯ»
3) Это шестизначные числа √271441=521
√27’14’41
-25
-214
2
2
204
-1041
1041
0
104
1
1
1) Делаю все точно также как и с пятизначными числами

«ПРИЁМЫ ДЕЛЕНИЯ»
1) Деление на 5; 50; 500 и т. д.
Заменю делитель на соответствующую дробь: т.к. 5 = 10/2; 50 = 100/2 и т.д. Теперь достаточно отделить у частного два знака после запятой и умножить на 2
Например, разделить 1750 на 50:
1750/50 = 1750*2/100 = 3500/100 = 35

«ПРИЕМЫ СЛОЖЕНИЯ И ВЫЧИТАНИЯ»
1) Это округления чисел
Допустим мне надо выполнить 589+758=?
1) Зная, что число 589 ближе к 600 => 600+758=1358
2) Но 1358 это не точный ответ, я из этого числа вычитаю то количество единиц, сколько я прибавили чтобы получить 600, то есть 1358-11=1347
Таким же способом и выполняется вычитания:
611-509=611-(510-1)=611-510+1=101+1=102
396-299=396-(300-1)=396-300+1=97

«ПРИЁМЫ СЛОЖЕНИЯ И ВЫЧИТАНИЯ»
2) Поразрядно
836+899=?
Складываю поразрядно:
800+800=1600
30+90=120
6+9=15
1600+120+15=1735
Если в уменьшаемом число единиц каждого разряда
больше единиц соответствующего разряда вычитаемого,
то вычитание выполняется поразрядно
678-564= (600-500)+(70-60)+(8-4)=100+10+4=114

ВЫВОД
Знание приемов быстрого счета позволяет упрощать вычисления, экономить время, развивает логическое мышление и гибкость ума.
Освоение вычислительных навыков развивает память и помогает усваивать предметы математического цикла.
Памятка для быстрого счета будет полезна для учащихся (выпускников).

ЛИТЕРАТУРА
https://vk.com/doc3260116_546038518?hash=1f0192effdef24d1cf&dl=0f22c0c03d5f581460
https://www.rdita.kg/files/books/эрудит/bendzhamin_a_matemagiya_sekrety_mental_noy_matematiki.pdf