Содержание
- 2. 1.Общая постановка задачи; 2.Классификация задач нелинейного программирования; 3.Классификация методов нелинейного программирования; 4.Области применения нелинейного программирования. План:
- 3. Математическая модель задачи нелинейного программирования в общем виде формулируется следующим образом: найти вектор , удовлетворяющий системе
- 4. По числу переменных: Задача одномерной оптимизации (ЗОО); Задача многомерной оптимизации (ЗМО). По виду ограничений: Задача безусловной
- 5. Для задачи нелинейного программирования в отличие от задач линейного программирования нет единого метода решения. В зависимости
- 6. Для решения задачи нелинейного программирования было предложено много методов, которые можно классифицировать по различным признакам. По
- 7. По типу информации, используемой в алгоритме поиска экстремума методы делятся на: методы прямого поиска, т.е. методы,
- 8. Из нелинейного программирования наиболее разработаны задачи, в которых система ограничений линейная, а целевая функция нелинейная. Однако
- 9. При решении задач нелинейного программирования для целевой функции необходимо определить глобальный максимум или глобальный минимум. Глобальный
- 10. ЗНП встречается в естественных науках, технике, экономике, математике, в сфере деловых отношений и в науке управления
- 11. В такой общей постановке определение точных форм функций может оказаться невозможным; однако в конкретных применениях точный
- 12. Метод «затраты—эффективность» также укладывается в схему НЛП. Метод был разработан для использования при принятии решений в
- 13. Упомянутые применения НЛП концентрированы на задачах о принятии решений. Действительно, существенная сторона НЛП заключается в том,
- 14. Очевидные задачи НЛП часто возникают в науке. В физике, например, целевой функцией может быть потенциальная энергия,
- 16. Скачать презентацию













 Показательные уравнения: типы и методы решения
Показательные уравнения: типы и методы решения Пример записи решения задания к Части I РГР №1
Пример записи решения задания к Части I РГР №1 Математическая игра «Звездный час»
Математическая игра «Звездный час» Распредели предметы поровну
Распредели предметы поровну Задачи на разрезание и перекраивание фигур
Задачи на разрезание и перекраивание фигур Соотношения между сторонами и углами прямоугольного треугольника. Синус, косинус, тангенс и котангенс острого угла
Соотношения между сторонами и углами прямоугольного треугольника. Синус, косинус, тангенс и котангенс острого угла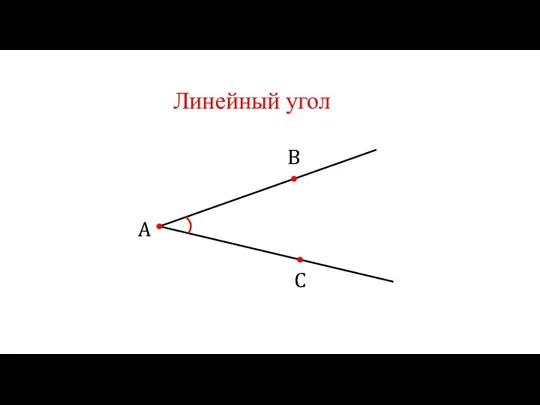 Двугранный угол. Линейный угол
Двугранный угол. Линейный угол Признаки делимости
Признаки делимости Совокупность математических методов для изучения свойств кубика Рубика
Совокупность математических методов для изучения свойств кубика Рубика Степенная функция. Определение
Степенная функция. Определение Элементы комбинаторики
Элементы комбинаторики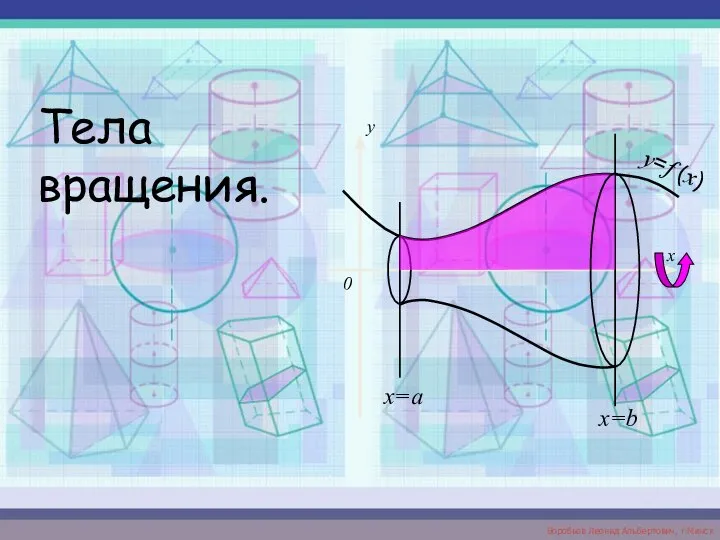 Тела вращения
Тела вращения Связь сложения и умножения
Связь сложения и умножения Властивість бісектриси трикутника
Властивість бісектриси трикутника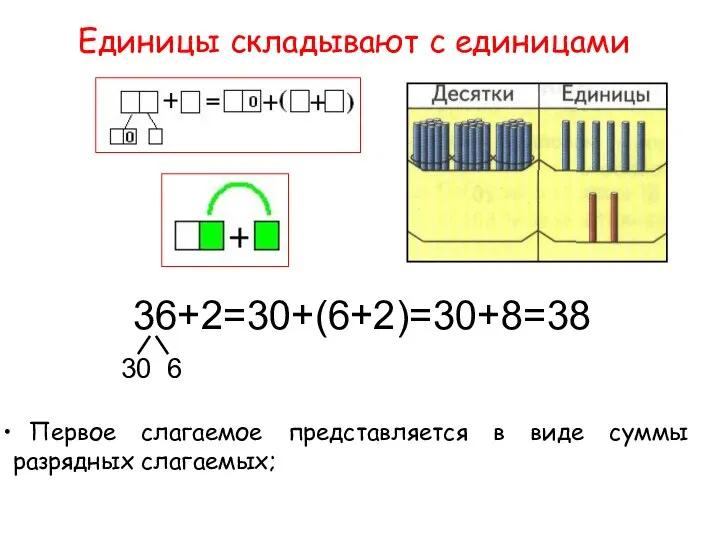 Алгоритм вычислений
Алгоритм вычислений Золотое сечение
Золотое сечение Выражения. Подготовка к ЕГЭ. Задачи
Выражения. Подготовка к ЕГЭ. Задачи Деление и обобщение понятий. Круги Эйлера-Венна.
Деление и обобщение понятий. Круги Эйлера-Венна. Математическая игра Петергофская мозаика 5 класс
Математическая игра Петергофская мозаика 5 класс Решение задач
Решение задач Презентация на тему ЛОГАРИФМ ЧИСЛА
Презентация на тему ЛОГАРИФМ ЧИСЛА  Касательная к окружности. Решение задач
Касательная к окружности. Решение задач Параллельные прямые
Параллельные прямые Обратная матрица
Обратная матрица Старинные русские меры длины
Старинные русские меры длины Пирамида. Высрта пирамиды
Пирамида. Высрта пирамиды Потенцирование логарифмических выражений
Потенцирование логарифмических выражений Свойство противоположных сторон четырехугольника
Свойство противоположных сторон четырехугольника