Однородные тригонометрические уравнения

Однородное тригонометрическое уравнение -это уравнение двух видов:
a sin x + b cos x = 0 (однородное уравнение первой степени), либо
a sin2 x + b sin x cos x + c cos2 x = 0 (однородное уравнение второй степени)

Пример:
Решим уравнение 2 sin x – 3 cos x = 0.
Алгоритм решения однородного уравнения первой степени a sin x + b cos x = 0:
1) разделить обе части уравнения на cos x
2) решить получившееся уравнение

Пример: Решить уравнение
sin2 x – 3 sin x cos x + 2 cos2 x = 0
Делим обе части уравнения на cos2 x
Получим, tg2 х - 3tgх + 2 = 0
Решаем квадратное уравнение относительно tgх
tgх = у, у2 – 3у + 2 = 0, Д = 1,у1 = 2, у2 = 2
Решаем теперь относительно х,
х1 = arctg 2 + Пn
х2 = arctg 1 + Пn
х2 = П/4 + Пn

Все необходимые формулы на слайдах № 7-11
Решить самостоятельно
1.-sin2x + cos 2x - cos2x = 0
2.sin2 x + sin x cos x = 0
3.( sin x + cos x) 2 = cos2 x
4. sin2x + 4 cos 2x = 1
5. sin2x + 2cos 2x = 1

Условие: в уравнении должно быть выражение вида a sin2 x.
Если его нет, то уравнение решается методом разложения на множители.
1) Разделить обе части уравнения на cos2 x
2) Ввести новую переменную у, заменяющую tg x (у = tg x)
3) Решить получившееся уравнение
Алгоритм решения однородного уравнения второй степени
a sin2 x + b sin x cos x + c cos2 x = 0

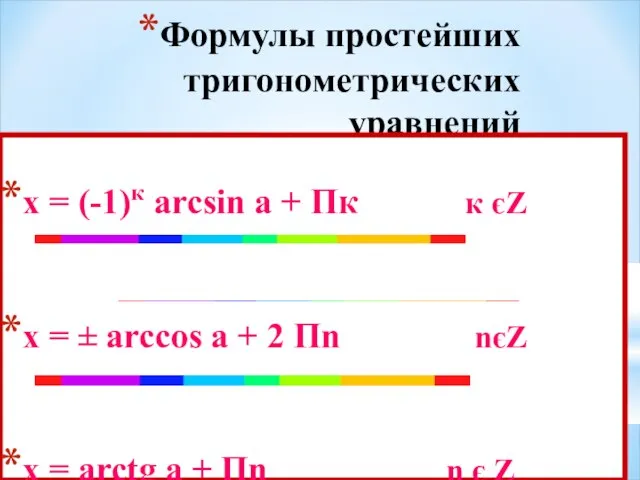
Формулы простейших тригонометрических уравнений
х = (-1)к arcsin а + Пк к єZ
х = ± arccos а + 2 Пn nєZ
х = аrctg а + Пn n є Z

Особые случаи для синуса