Содержание
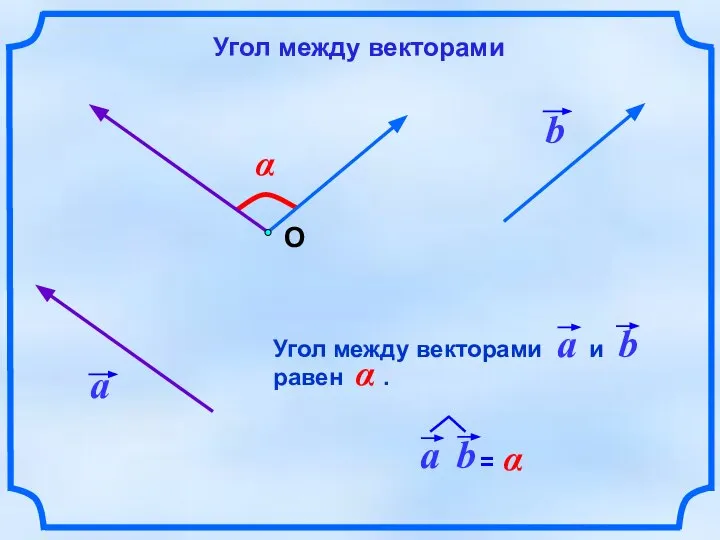
- 2. α О Угол между векторами
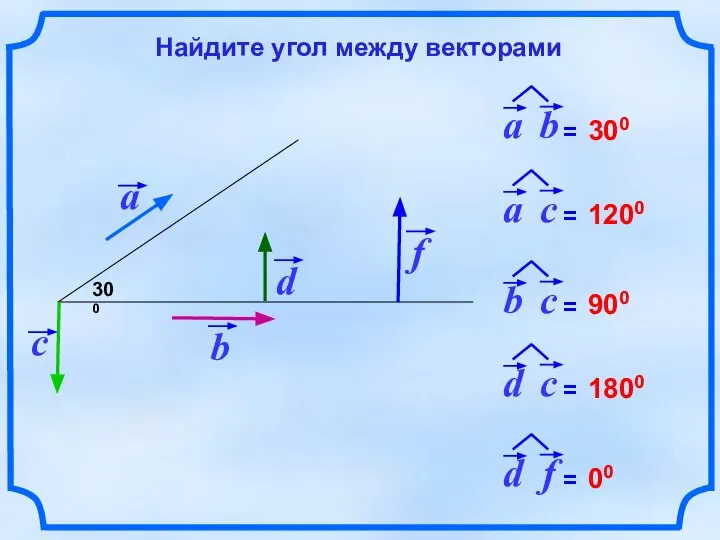
- 3. 300 300 1200 900 1800 00 Найдите угол между векторами
- 4. Скалярное произведение векторов – число (скаляр). Скалярным произведением двух векторов называется произведение их длин на косинус
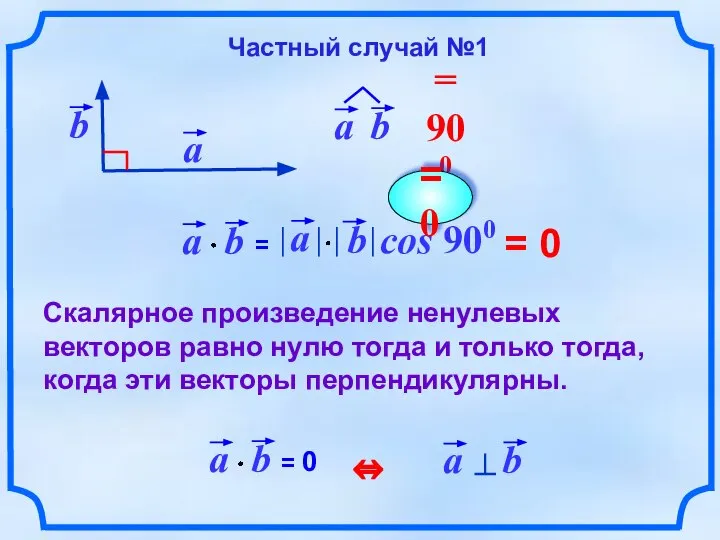
- 5. = 0 Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
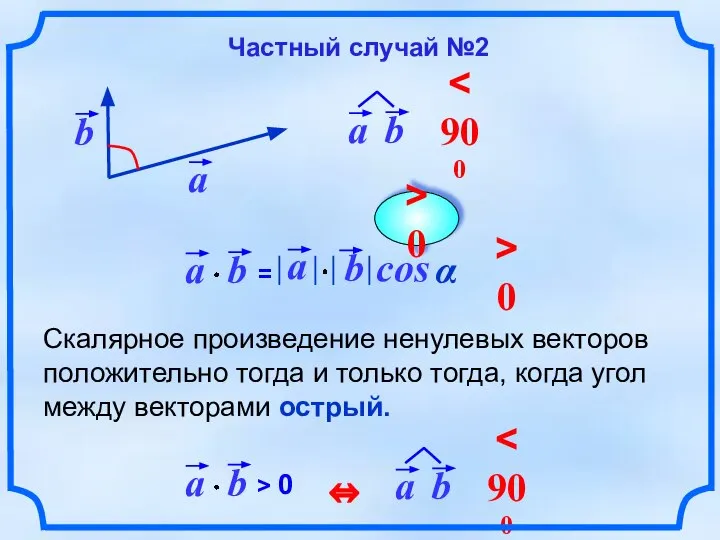
- 6. Скалярное произведение ненулевых векторов положительно тогда и только тогда, когда угол между векторами острый. cos α
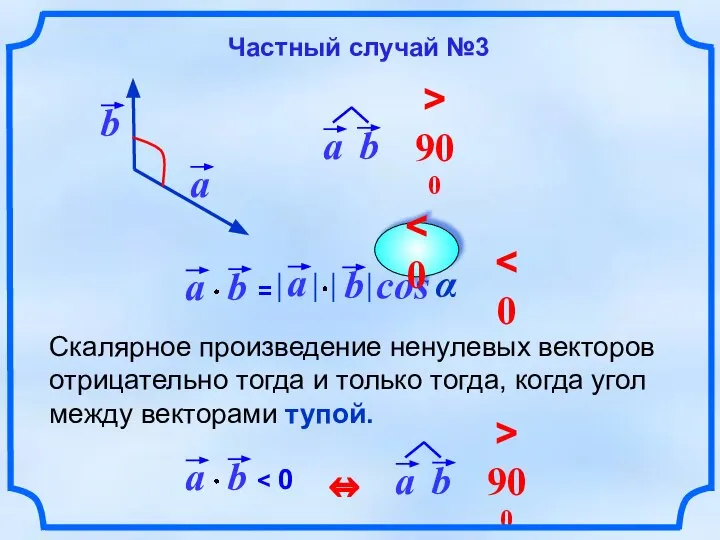
- 7. Скалярное произведение ненулевых векторов отрицательно тогда и только тогда, когда угол между векторами тупой. cos α
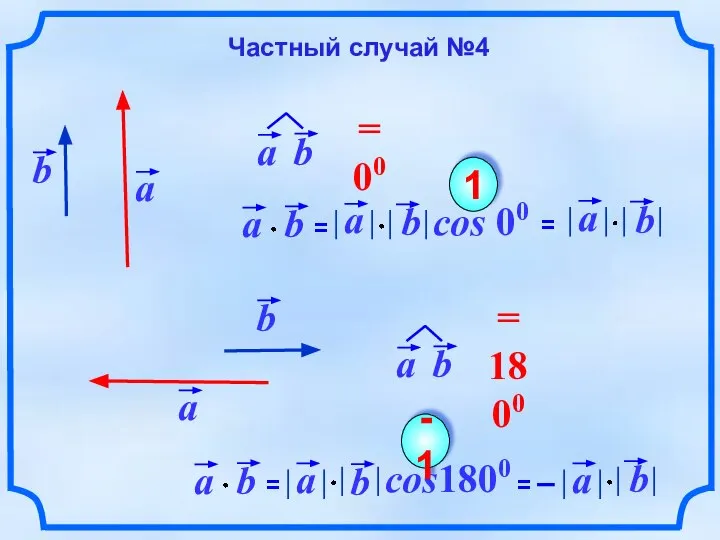
- 8. cos 00 1 cos1800 -1 Частный случай №4
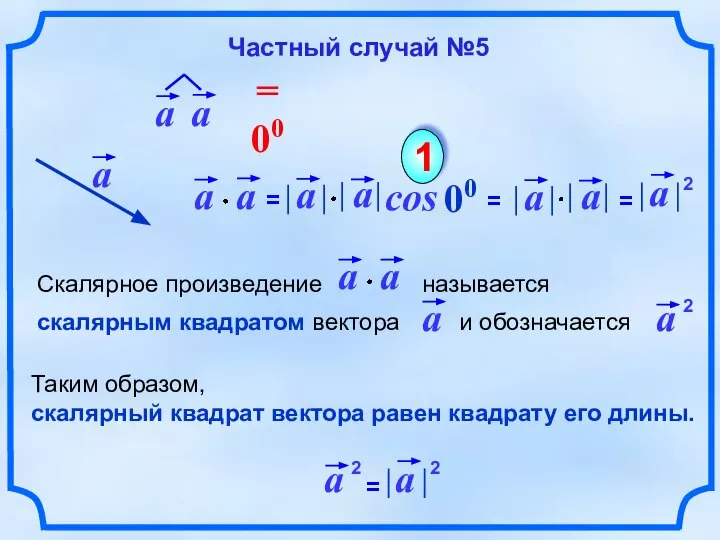
- 9. cos 00 1 Таким образом, скалярный квадрат вектора равен квадрату его длины. Частный случай №5 2
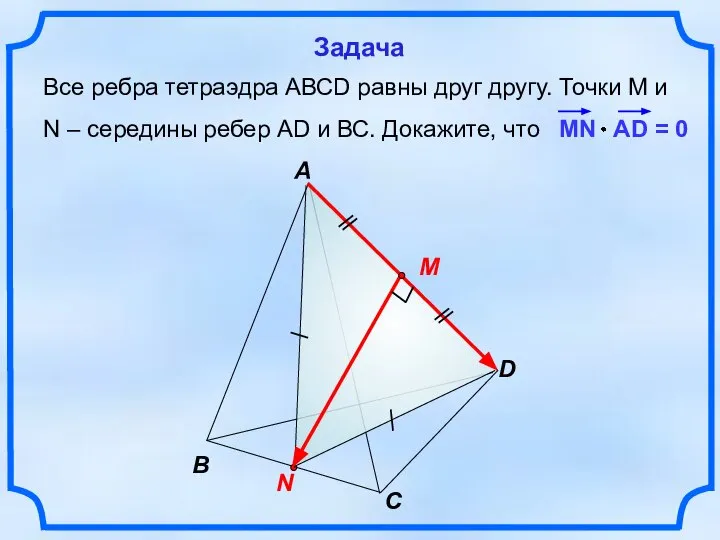
- 10. Все ребра тетраэдра АВСD равны друг другу. Точки М и N – середины ребер АD и
- 11. Формула для нахождения скалярного произведения через координаты векторов = x1x2 + y1y2 + z1z2
- 12. Пример №1 Найти скалярное произведение векторов: a {-6; 9; 5} b {-1; 0; 7}
- 13. Пример №2 Найти скалярное произведение векторов: a {0; 0; 4} b {22; 1; 8}
- 14. Пример №3 Найти скалярное произведение векторов: a {1; 7; 9} b {-2; 4; 0}
- 15. Проверочная работа 1. Найти скалярное произведение векторов: a {1; 10; 7} b {0; 7; 0}
- 16. Проверочная работа 2. Найти скалярное произведение векторов: a {7; 25; 0} b {11; 0; 54}
- 17. Проверочная работа 3. Найти скалярное произведение векторов: a {|-2|; 0; |3|} b {1; |-11|; 1}
- 18. Проверочная работа 4. Найти скалярное произведение векторов: a {sin(900); 2; 3} b {3; 2; 1}
- 20. Скачать презентацию









 Занятие 1_2022
Занятие 1_2022 Презентация на тему Прибавление числа 4 (1 класс)
Презентация на тему Прибавление числа 4 (1 класс)  Тригонометрические функции
Тригонометрические функции Значение слова алгоритм
Значение слова алгоритм Преобразование графиков тригонометрических функций в среде Microsoft Excel. Свойства функций
Преобразование графиков тригонометрических функций в среде Microsoft Excel. Свойства функций Классическое определение вероятности
Классическое определение вероятности Шар и сфера
Шар и сфера Опрос общественного мнения. Повторение действий с дробями
Опрос общественного мнения. Повторение действий с дробями Презентация на тему Число 0 Цифра 0
Презентация на тему Число 0 Цифра 0  Функціональні рівняння
Функціональні рівняння izmerenie_otrezkov_7_klass
izmerenie_otrezkov_7_klass Число один. Знаки + или -
Число один. Знаки + или - Определители второго и третьего порядка. 11 класс
Определители второго и третьего порядка. 11 класс Основные типы дифференциальных уравнений первого порядка
Основные типы дифференциальных уравнений первого порядка Решение стереометрических задач методом координат
Решение стереометрических задач методом координат Дифференциальные исчисления функции одной независимой переменной
Дифференциальные исчисления функции одной независимой переменной Методика изучения площади
Методика изучения площади Математическая логика
Математическая логика Площадь поверхности цилиндра
Площадь поверхности цилиндра Обработка результатов измерения отклонений от круглости
Обработка результатов измерения отклонений от круглости Аппроксимация функций. Метод Лагранжа
Аппроксимация функций. Метод Лагранжа Интерактивный тренажёр Счет в пределах 15
Интерактивный тренажёр Счет в пределах 15 Урок математики в 5 классе
Урок математики в 5 классе Вычисление неопределенного интеграла
Вычисление неопределенного интеграла 1_2_opredeliteli (1)
1_2_opredeliteli (1) Интегрирование методом внесения под знак дифференциала
Интегрирование методом внесения под знак дифференциала Решение треугольников
Решение треугольников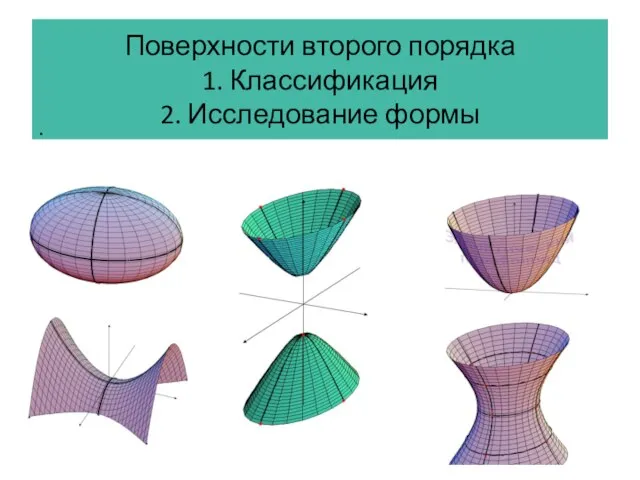 Поверхности второго порядка
Поверхности второго порядка