Определители второго и третьего порядков

Мы начинаем изучение курса аналитической геометрии. Содержательно весь курс можно разбить на четыре большие части:
1
векторная алгебра (лекции 2–6); прямые и плоскости (лекции 7–9); квадрики на плоскости (лекции 10–13);
квадрики в пространстве (лекции 14–17).
Данная лекция не входит ни в одну из этих частей и носит вспомогательный характер. В ней вводится понятие определителя для квадратных матриц второго и третьего порядков, указываются некоторые свойства этих определителей и демонстрируется, как они возникают и используются при решении систем двух линейных уравнений с двумя неизвестными и трех линейных уравнений с тремя неизвестными. Этот материал пригодится нам уже в самое ближайшее время. Более общее понятие определителей произвольного порядка, их свойства и использование при решении систем n линейных уравнений с n неизвестными изучаются в курсе алгебры.
Лекция 1: Определители второго и третьего порядков

Понятие матрицы (1)
Мы начнем с важного для дальнейшего понятия матрицы.
Определение
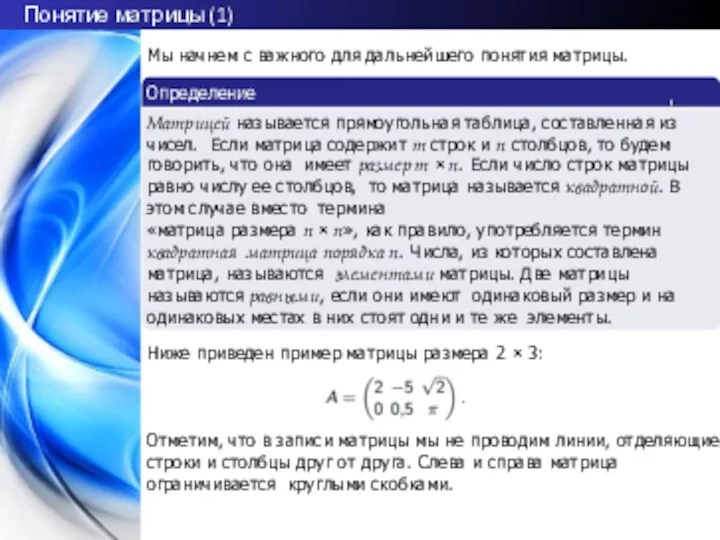
Матрицей называется прямоугольная таблица, составленная из чисел. Если матрица содержит m строк и n столбцов, то будем говорить, что она имеет размер m × n. Если число строк матрицы равно числу ее столбцов, то матрица называется квадратной. В этом случае вместо термина
«матрица размера n × n», как правило, употребляется термин квадратная матрица порядка n. Числа, из которых составлена матрица, называются элементами матрицы. Две матрицы называются равными, если они имеют одинаковый размер и на одинаковых местах в них стоят одни и те же элементы.
Ниже приведен пример матрицы размера 2 × 3:
Отметим, что в записи матрицы мы не проводим линии, отделяющие строки и столбцы друг от друга. Слева и справа матрица ограничивается круглыми скобками.
Лекция 1: Определители второго и третьего порядков

Понятие матрицы (2)
Для обозначения элементов матриц применяется двойная индексация, при этом первый индекс означает номер строки, а второй — номер столбца, в
которых стоит данный элемент. Например, a12 — элемент, стоящий в первой строке и втором столбце. Произвольная матрица размера m × n обозначается следующим образом:
Кратко эта матрица записывается в виде A = (aij ), а если важно указать ее размер — то в виде A = (aij )m×n .
Определение
Если A = (aij ) — квадратная матрица порядка n, то элементы
a11, a22, . . . , ann образуют главную диагональ матрицы A, а элементы
a1n, a2 n−1, . . . , an1 — ее побочную диагональ.
Лекция 1: Определители второго и третьего порядков

Определители второго порядка

Определители второго порядка и системы линейных уравнений
Определители возникли в теории систем линейных уравнений. Покажем, как применяется понятие определителя второго порядка к решению системы двух линейных уравнений с двумя неизвестными. Такая система в общем виде может быть записана следующим образом:
Определение
Матрица A = (aij ), составленная из коэффициентов системы (1), называется основной матрицей этой системы. Определитель этой матрицы (т. е. определитель ∆) называется определителем системы (1).
Заметим, что
определитель ∆i (при i = 1, 2) получается из определителя ∆ заменой
i -го столбца основной матрицы на столбец свободных членов.
Б.М.Верников

Теорема Крамера для систем второго порядка (1)
Лекция 1: Определители второго и третьего порядков

Теорема Крамера для систем второго порядка (2)

Определители третьего порядка (1)

Определители третьего порядка (2)

Правило треугольников

Определители третьего порядка и системы линейных уравнений
Б.М.Верников

Теорема Крамера для систем третьего порядка

Разложение определителя третьего порядка по строке или столбцу (1)

Разложение определителя третьего порядка по строке или столбцу (2)

Транспонирование матрицы

Свойства определителей

Доказательство свойств 1) и 2)

Доказательство свойств 3) и 4)