Содержание
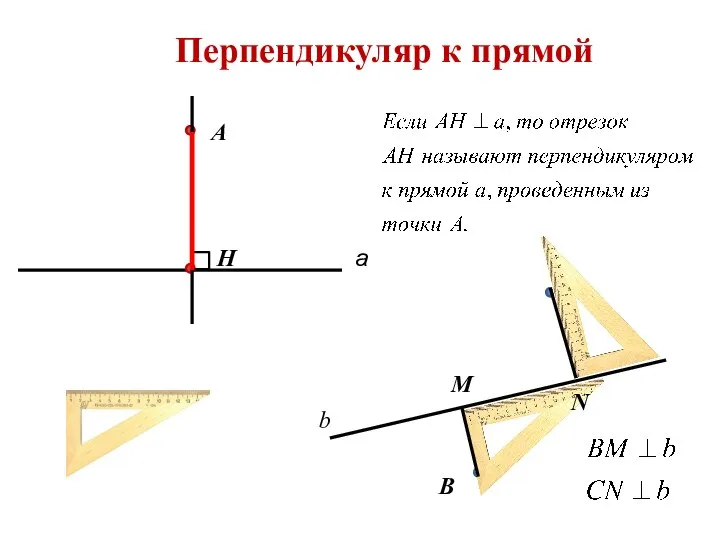
- 2. Перпендикуляр к прямой а А Н В С M N b
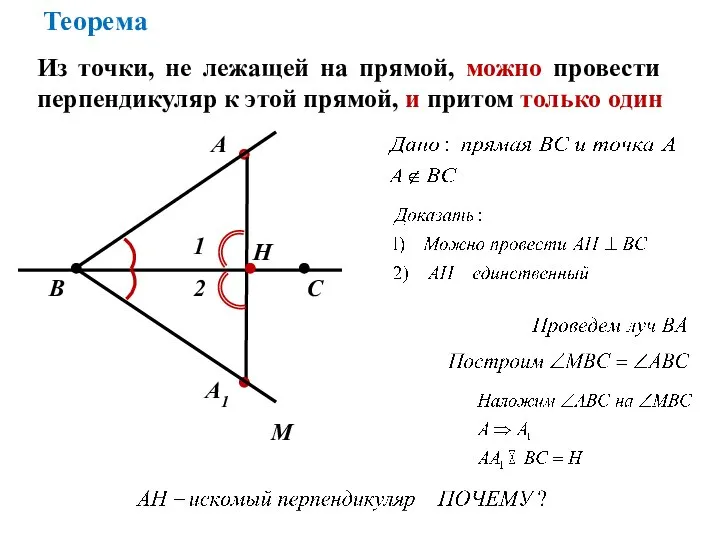
- 3. А Н В С M Из точки, не лежащей на прямой, можно провести перпендикуляр к этой
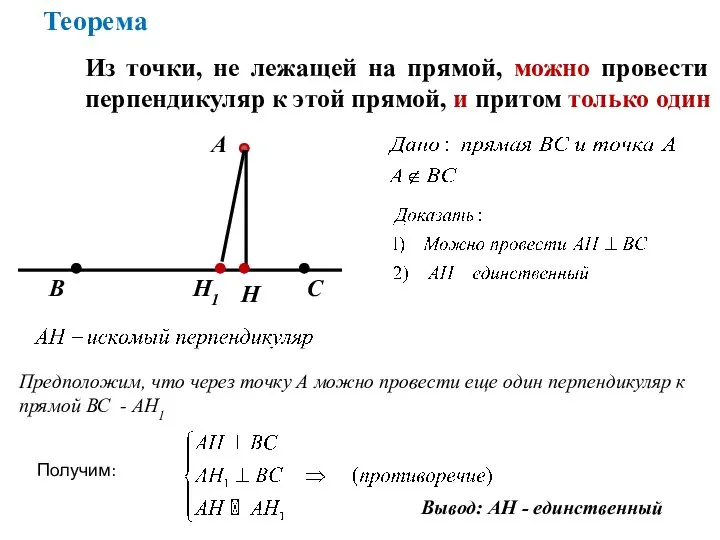
- 4. А Н В С Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой,
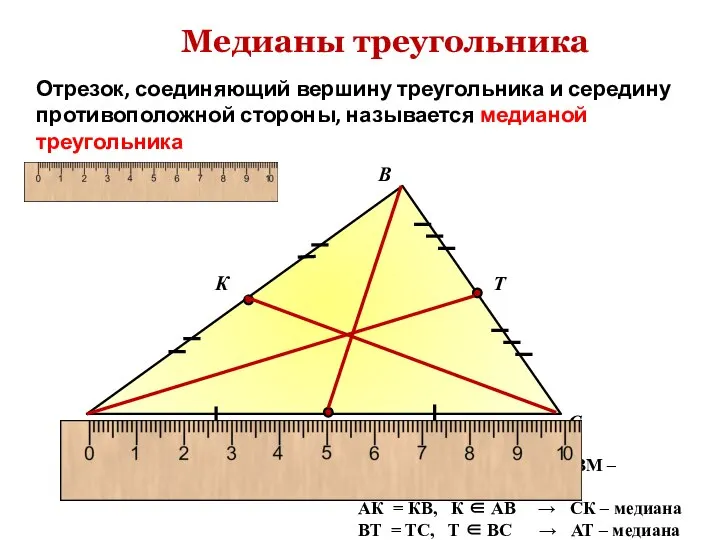
- 5. Медианы треугольника Отрезок, соединяющий вершину треугольника и середину противоположной стороны, называется медианой треугольника А В С
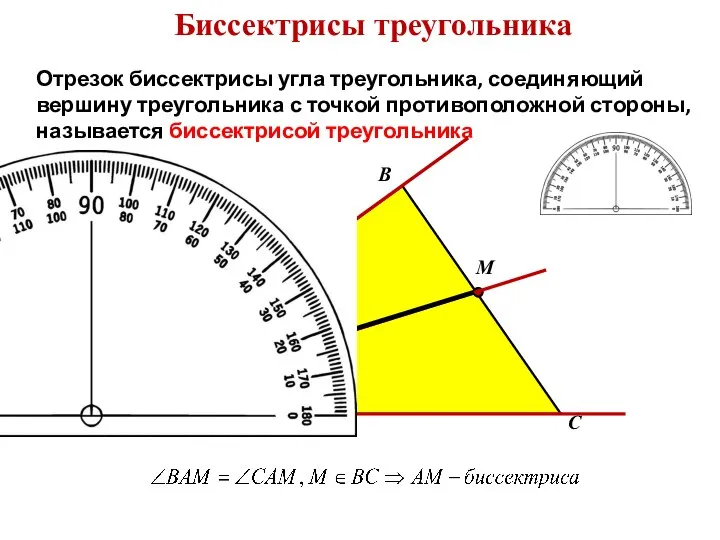
- 6. Биссектрисы треугольника Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника
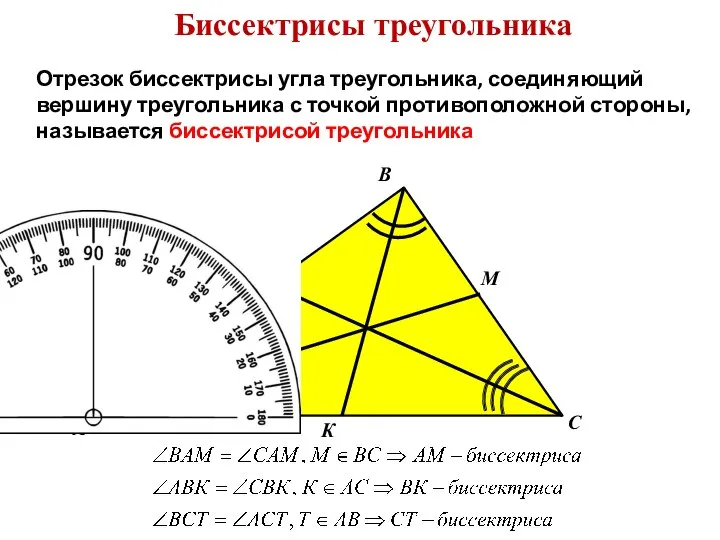
- 7. Биссектрисы треугольника Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника
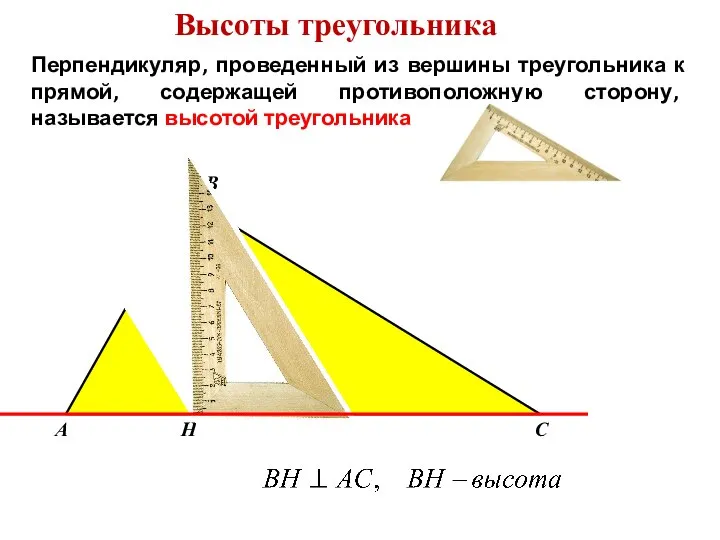
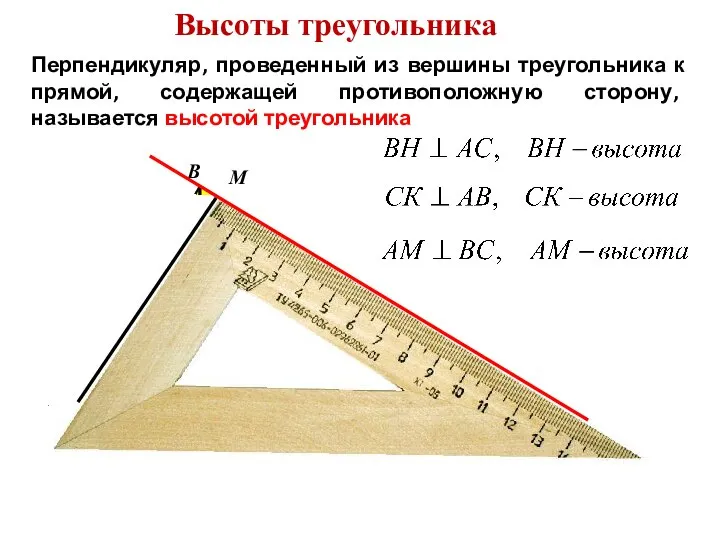
- 8. Высоты треугольника Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника А
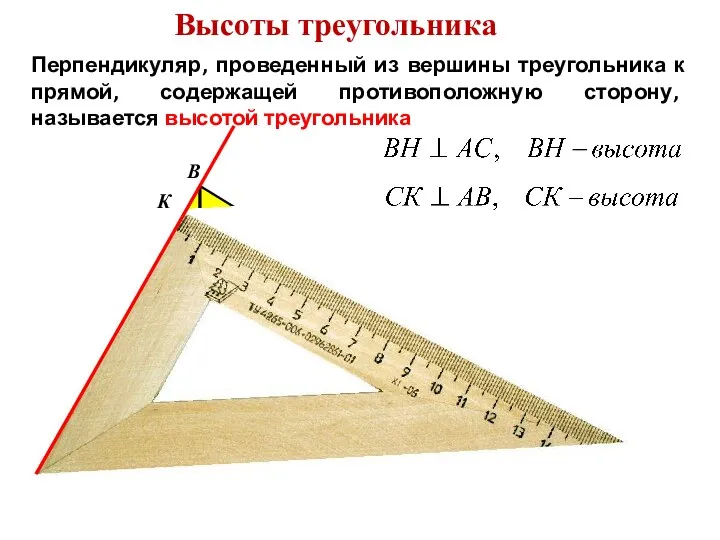
- 9. Высоты треугольника Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника А
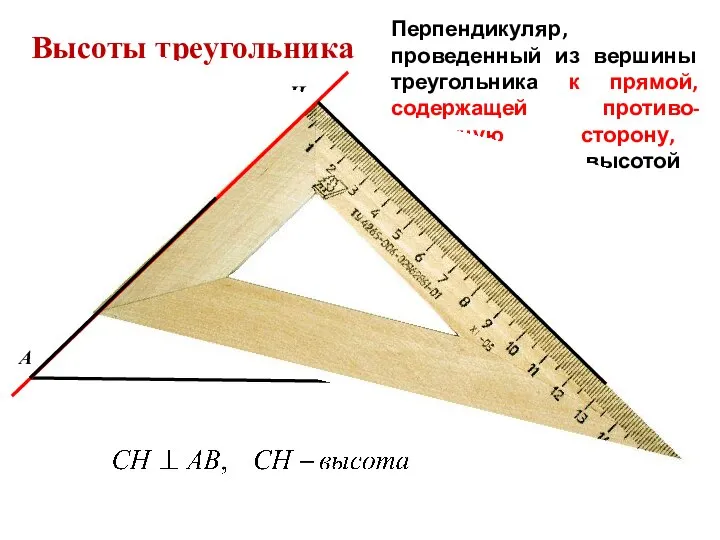
- 10. Высоты треугольника Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника А
- 11. Высоты треугольника Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противо-положную сторону, называется высотой треугольника А
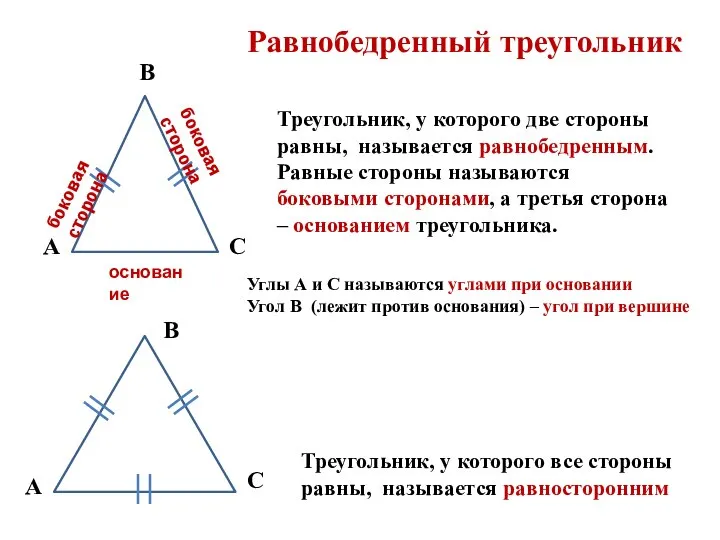
- 12. Равнобедренный треугольник Треугольник, у которого две стороны равны, называется равнобедренным. Равные стороны называются боковыми сторонами, а
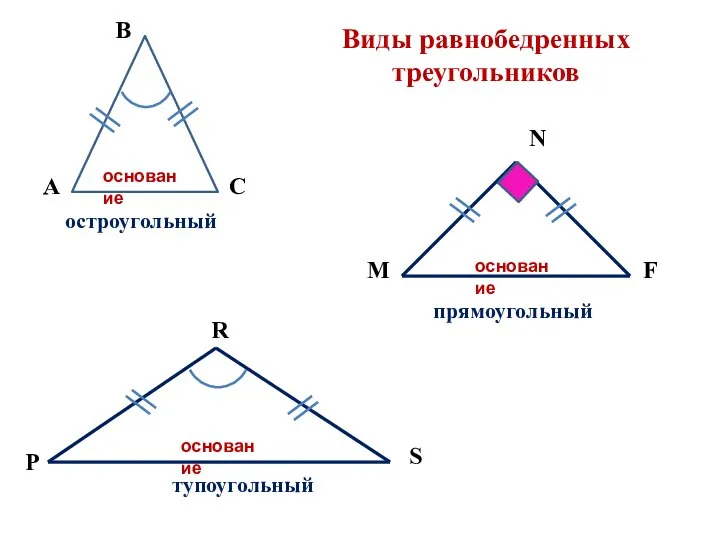
- 13. Виды равнобедренных треугольников остроугольный А В С основание M F N основание основание R P S
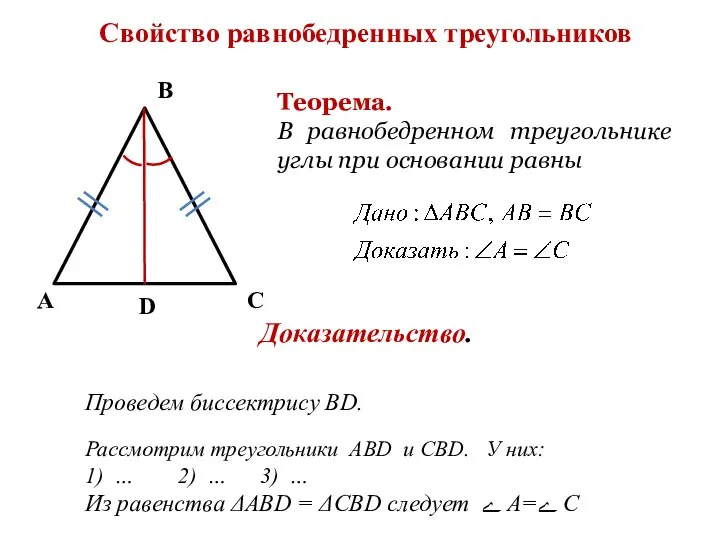
- 14. Свойство равнобедренных треугольников А В С Теорема. В равнобедренном треугольнике углы при основании равны D Доказательство.
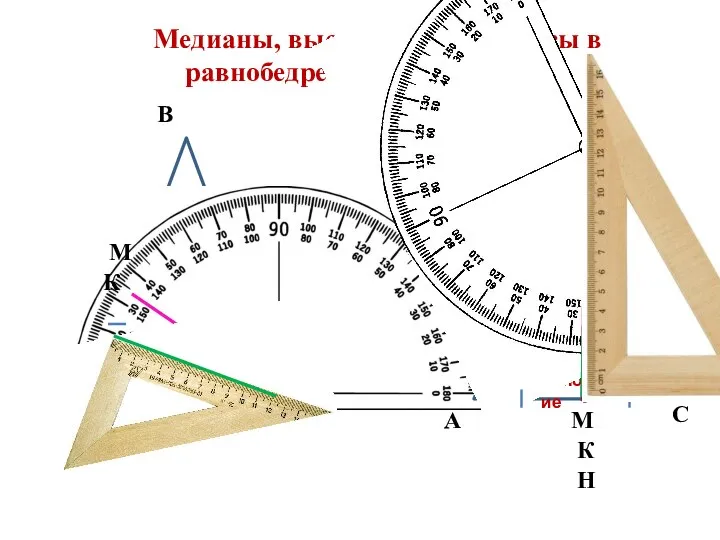
- 15. Медианы, высоты и биссектрисы в равнобедренном треугольнике А В С Н боковая сторона К M А
- 17. Скачать презентацию
 Среднее арифметическое. Размах. Мода
Среднее арифметическое. Размах. Мода Векторная алгебра
Векторная алгебра Презентация на тему Формулы (5 класс)
Презентация на тему Формулы (5 класс)  Презентация на тему Исследование функции с помощью производной
Презентация на тему Исследование функции с помощью производной  Аксиомы стереометрии
Аксиомы стереометрии Оператор Лапласа в полярных, цилиндрических и сферических системах координат
Оператор Лапласа в полярных, цилиндрических и сферических системах координат Обработка экспериментальных данных. Многофакторная регрессия. Лекция 7
Обработка экспериментальных данных. Многофакторная регрессия. Лекция 7 Виды четырехугольников
Виды четырехугольников Цилиндр
Цилиндр Симметрия вокруг нас
Симметрия вокруг нас Несобственные интегралы. Геометрические приложения определенного интеграла
Несобственные интегралы. Геометрические приложения определенного интеграла Метод координат в пространстве
Метод координат в пространстве Презентация на тему Правила дифференцирования
Презентация на тему Правила дифференцирования  Состав числа 8
Состав числа 8 Учимся писать цифры
Учимся писать цифры Длина окружности и число пи
Длина окружности и число пи Геометрия, как наука
Геометрия, как наука Чётные и нечётные числа. Подготовка к контрольной работе
Чётные и нечётные числа. Подготовка к контрольной работе Многозначная логика
Многозначная логика Prezentatsia_Microsoft_PowerPoint(1)
Prezentatsia_Microsoft_PowerPoint(1) Вычислительная математика. Практика №1
Вычислительная математика. Практика №1 Координатная плоскость. Графики
Координатная плоскость. Графики Уравнение прямой
Уравнение прямой Презентация на тему Нахождение неизвестного по двум разностям
Презентация на тему Нахождение неизвестного по двум разностям  Теорема Фалеса
Теорема Фалеса Решение уравнений. Тест
Решение уравнений. Тест Методы многокритериальной оптимизации
Методы многокритериальной оптимизации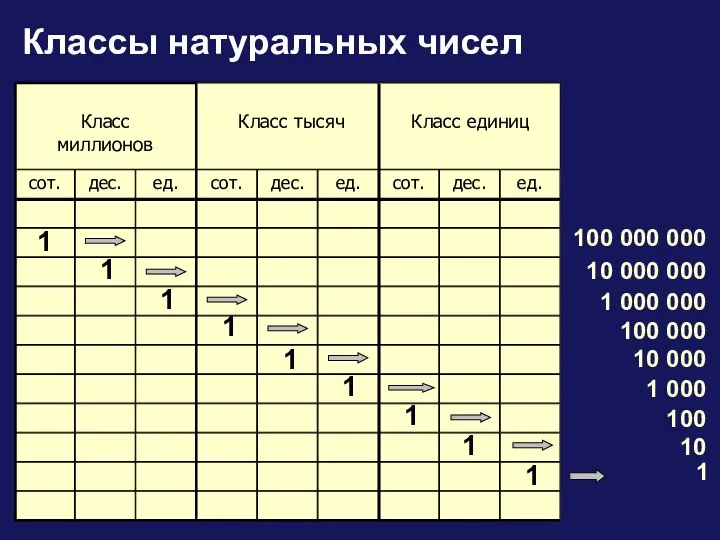 Классы натуральных чисел
Классы натуральных чисел