Содержание
- 2. Методические указания к лабораторным практикумам по курсам «Информационные технологии в химии и производстве ЭНМ» и «Хемометрика».
- 3. Цель работы Целью данной работы является освоение метода оптимизации технологических процессов по методу Бокса=Уилсона с применением
- 4. Введение Поиск оптимальных условий является одной из наиболее распространенных научно-технических задач. Процесс их решения называется процессом
- 5. Введение Данный метод является градиентным, т.е. движение в процессе оптимизации выполняется по градиенту. Градиент (от лат.
- 6. 1 Основные понятия и определения Независимые переменные величины, влияющие на протекание процесса, принято называть факторами. Это,
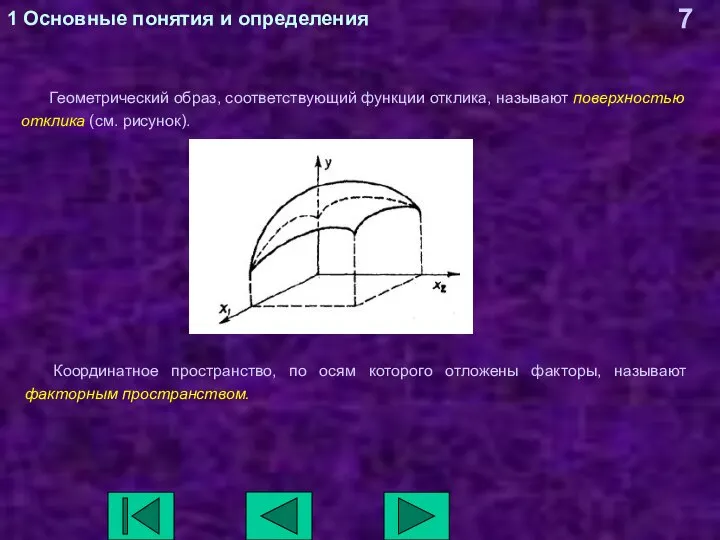
- 7. 1 Основные понятия и определения Геометрический образ, соответствующий функции отклика, называют поверхностью отклика (см. рисунок). Координатное
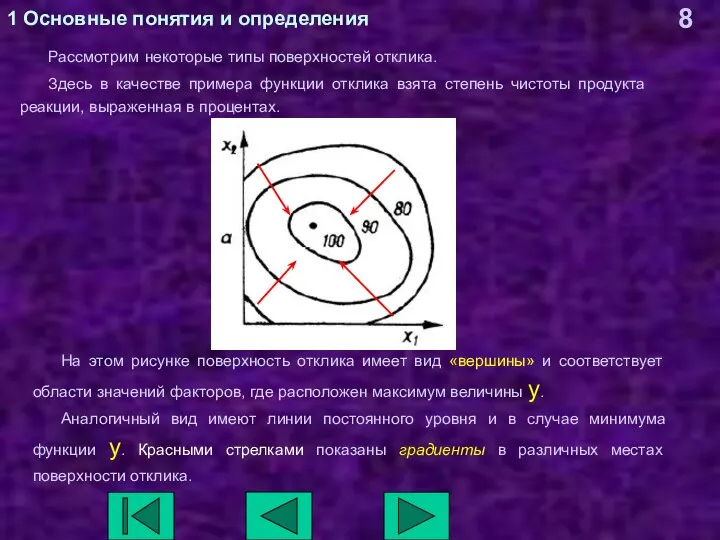
- 8. 1 Основные понятия и определения Рассмотрим некоторые типы поверхностей отклика. Здесь в качестве примера функции отклика
- 9. 1 Основные понятия и определения Поверхность, изображенная на этом рисунке характеризует плавное возрастание функции отклика с
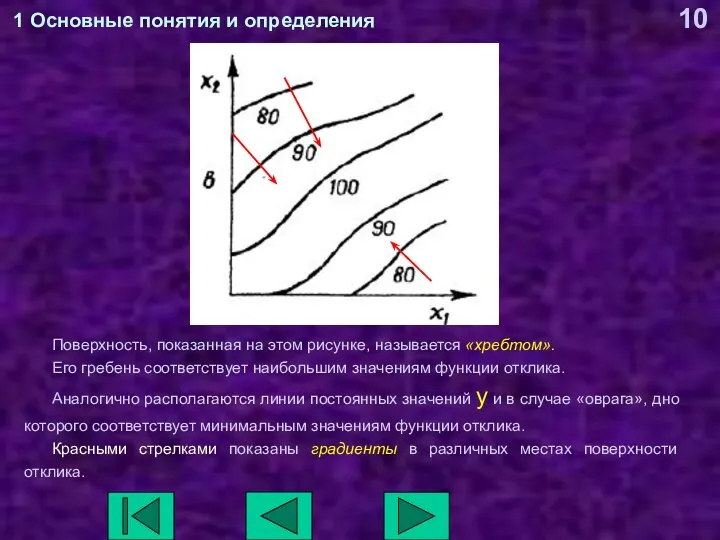
- 10. 1 Основные понятия и определения Поверхность, показанная на этом рисунке, называется «хребтом». Его гребень соответствует наибольшим
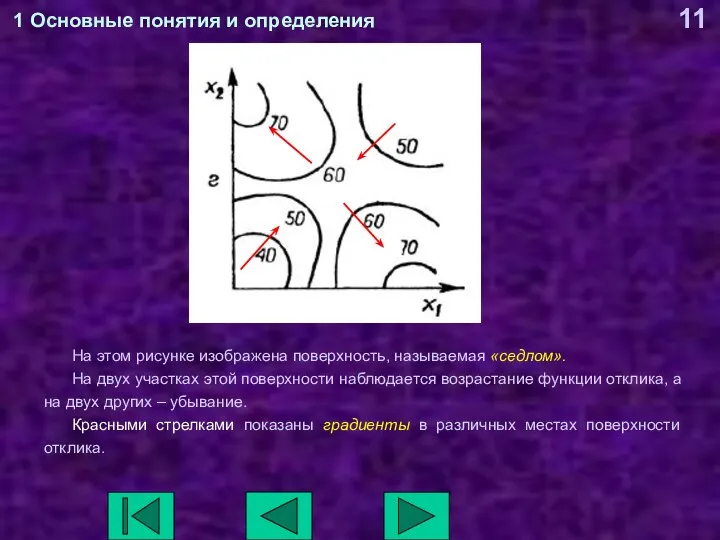
- 11. 1 Основные понятия и определения На этом рисунке изображена поверхность, называемая «седлом». На двух участках этой
- 12. 2 Сущность метода Бокса-Уилсона Сущность метода оптимизации по Боксу-Уилсону заключается в следующем (на примере двухфакторной оптимизации).
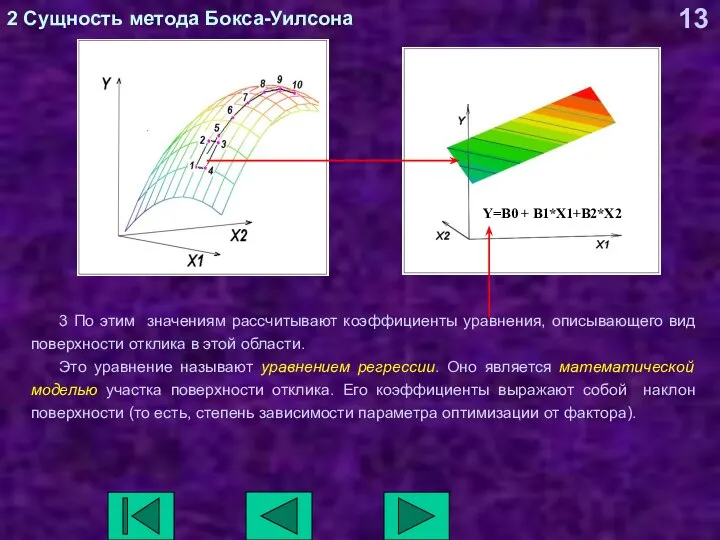
- 13. 2 Сущность метода Бокса-Уилсона 3 По этим значениям рассчитывают коэффициенты уравнения, описывающего вид поверхности отклика в
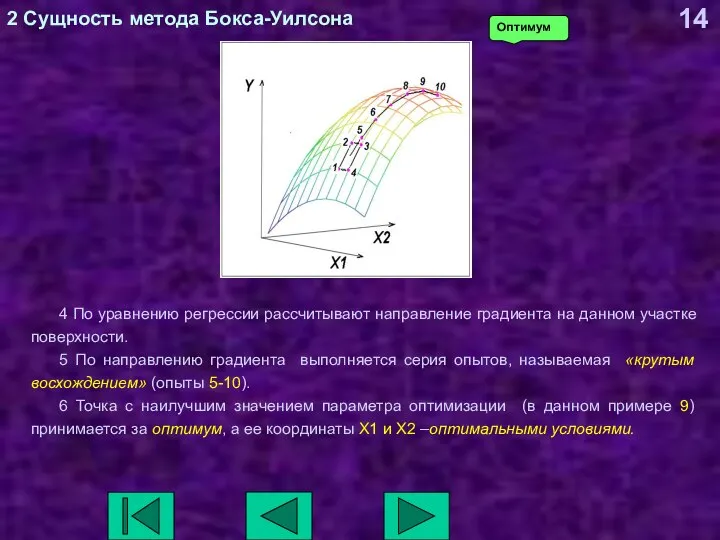
- 14. 2 Сущность метода Бокса-Уилсона 4 По уравнению регрессии рассчитывают направление градиента на данном участке поверхности. 5
- 15. 3 Принятие решений перед планированием эксперимента 3.1 Выбор области эксперимента При выборе области эксперимента прежде всего
- 16. 3 Принятие решений перед планированием эксперимента 3.2 Выбор основного уровня Наилучшим условиям, определенным из анализа априорной
- 17. 3 Принятие решений перед планированием эксперимента Для упрощения записи условий эксперимента и обработки экспериментальных данных масштабы
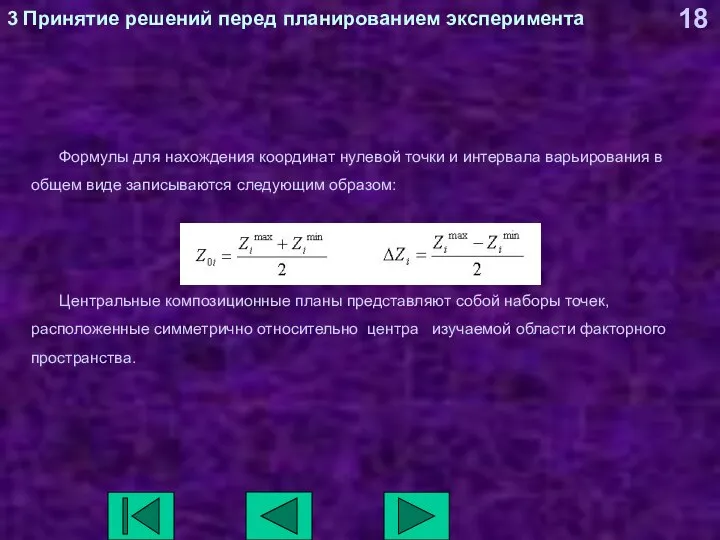
- 18. 3 Принятие решений перед планированием эксперимента Формулы для нахождения координат нулевой точки и интервала варьирования в
- 19. 3 Принятие решений перед планированием эксперимента Все расчеты, начиная от вычисления коэффициентов регрессии и кончая исследованием
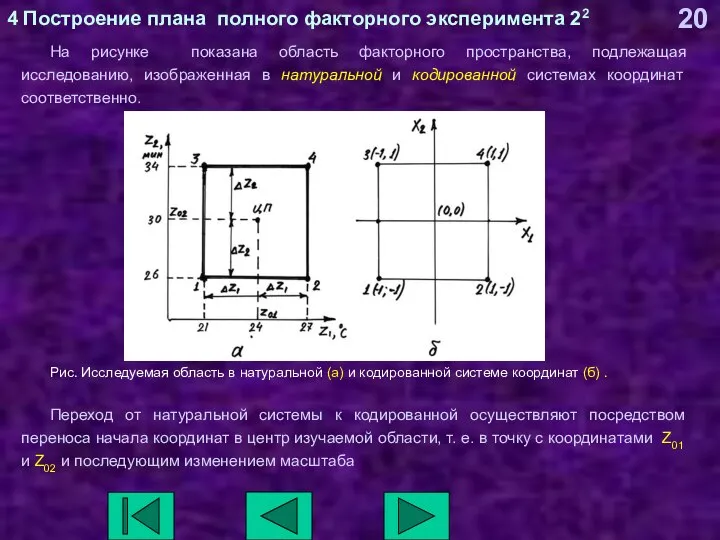
- 20. 4 Построение плана полного факторного эксперимента 22 На рисунке показана область факторного пространства, подлежащая исследованию, изображенная
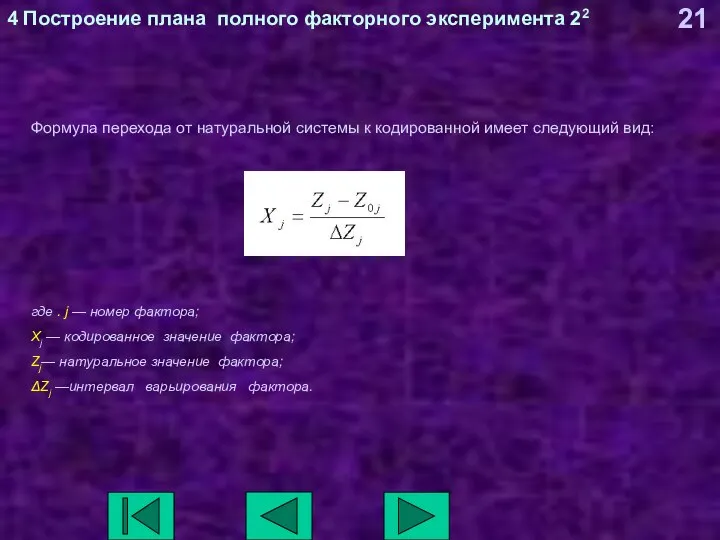
- 21. 4 Построение плана полного факторного эксперимента 22 Формула перехода от натуральной системы к кодированной имеет следующий
- 22. 4 Построение плана полного факторного эксперимента 22 Первый этап планирования эксперимента для получения линейной модели основан
- 23. 4 Построение плана полного факторного эксперимента 22 При проведении ПФЭ зададимся условиями, приведенными в данной таблице
- 24. 5 Построение матрицы планирования эксперимента 22 Нетрудно написать все сочетания уровней в эксперименте с двумя факторами.
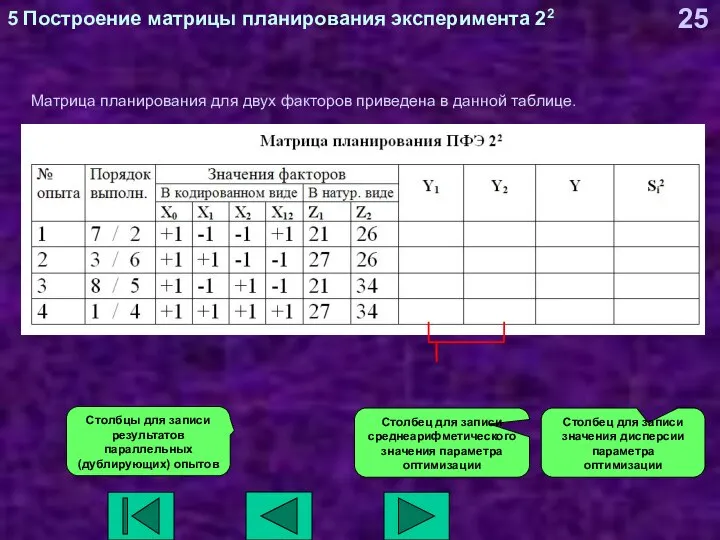
- 25. 5 Построение матрицы планирования эксперимента 22 Матрица планирования для двух факторов приведена в данной таблице. Столбцы
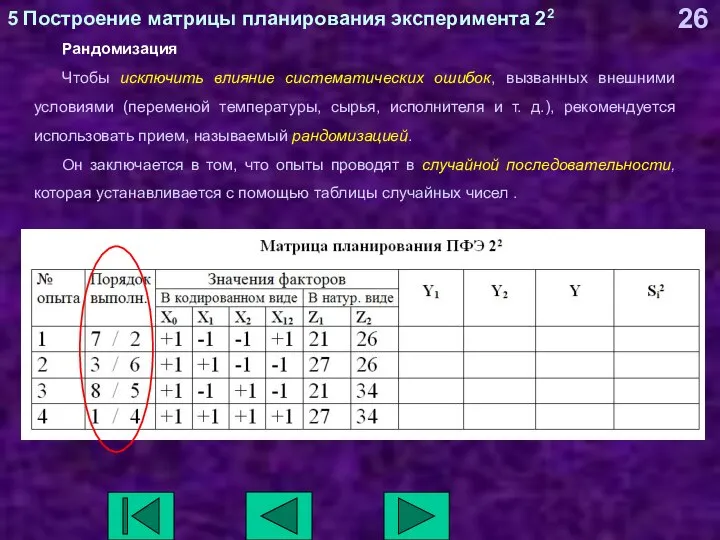
- 26. 5 Построение матрицы планирования эксперимента 22 Рандомизация Чтобы исключить влияние систематических ошибок, вызванных внешними условиями (переменой
- 27. 5 Упражнение 1. Обработка результатов эксперимента 22 Для изучения алгоритма обработки результатов полнофакторного эксперимента откройте файл-шаблон
- 28. 6 Графическая интерпретация процесса оптимизации Для лучшего понимания процесса оптимизации по Боксу-Уилсону и сознательного выполнения виртуального
- 29. 6 Графическая интерпретация процесса оптимизации На данных рисунках представлена графически сущность данного метода, разъясненная в следующих
- 30. 6 Графическая интерпретация процесса оптимизации На рисунке слева представлена процедура оптимизации в трехмерном пространстве. X1 и
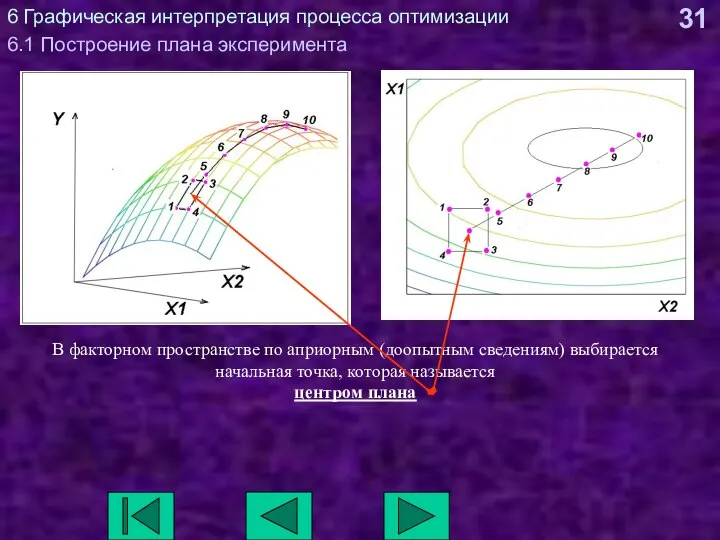
- 31. 6 Графическая интерпретация процесса оптимизации 6.1 Построение плана эксперимента В факторном пространстве по априорным (доопытным сведениям)
- 32. 6 Графическая интерпретация процесса оптимизации 6.1 Построение плана эксперимента Для каждого фактора (X1 и X2) выбирается
- 33. 6 Графическая интерпретация процесса оптимизации 6.1 Построение плана эксперимента Координаты каждой точки (1, 2, 3, 4)
- 34. 6 Графическая интерпретация процесса оптимизации 6.2 Получение математической модели Полученные в результате этих опытов значения параметра
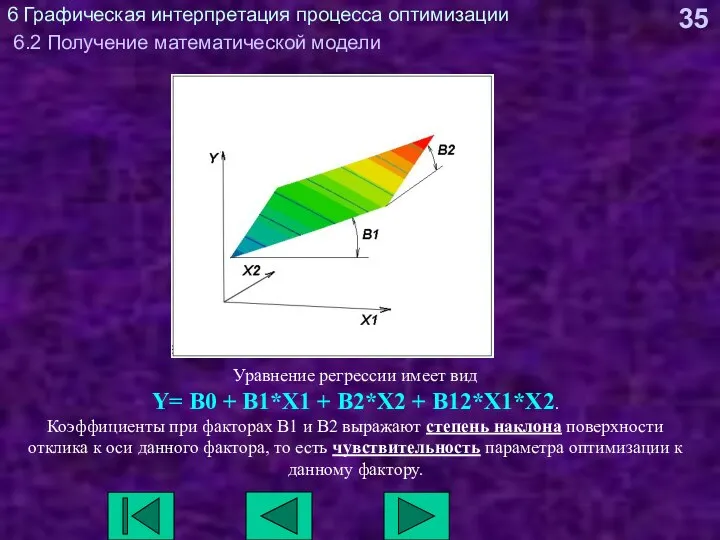
- 35. 6 Графическая интерпретация процесса оптимизации 6.2 Получение математической модели Уравнение регрессии имеет вид Y= B0 +
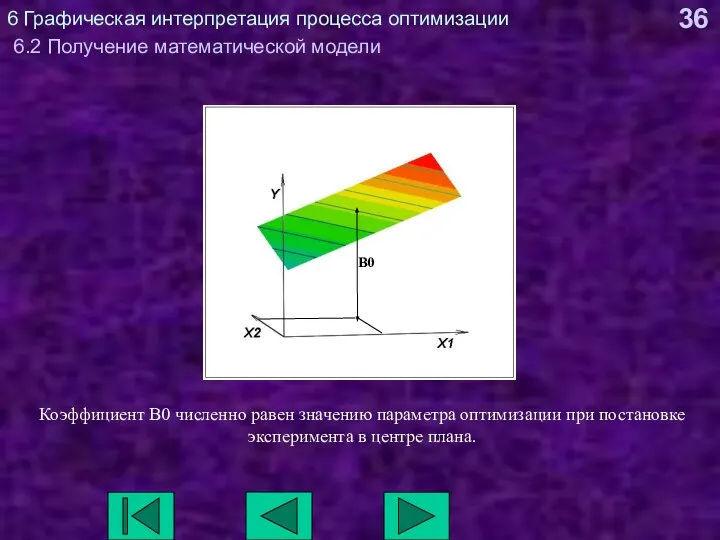
- 36. 6 Графическая интерпретация процесса оптимизации 6.2 Получение математической модели Коэффициент B0 численно равен значению параметра оптимизации
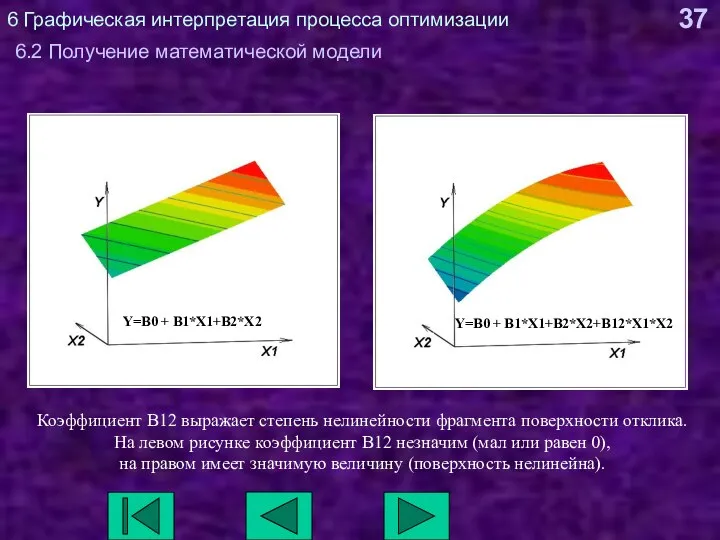
- 37. 6 Графическая интерпретация процесса оптимизации 6.2 Получение математической модели Коэффициент B12 выражает степень нелинейности фрагмента поверхности
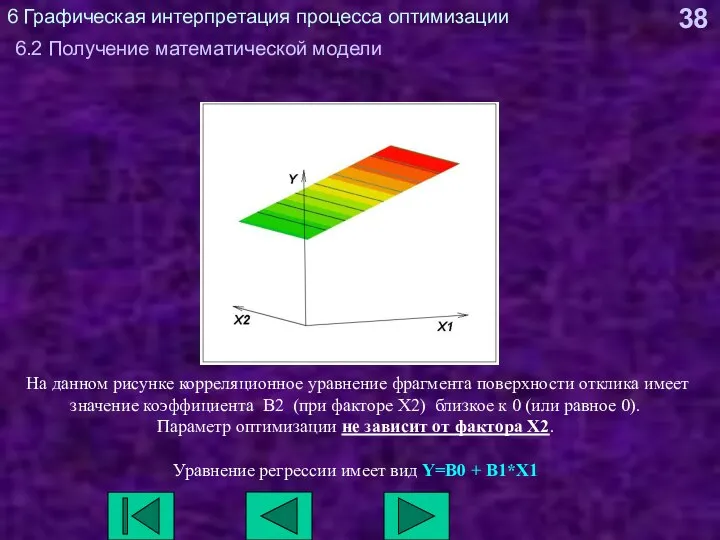
- 38. 6 Графическая интерпретация процесса оптимизации 6.2 Получение математической модели На данном рисунке корреляционное уравнение фрагмента поверхности
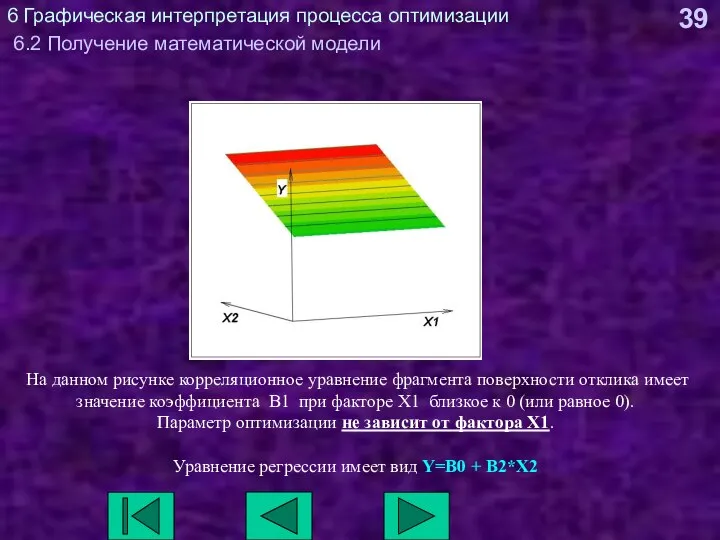
- 39. 6 Графическая интерпретация процесса оптимизации 6.2 Получение математической модели На данном рисунке корреляционное уравнение фрагмента поверхности
- 40. 6 Графическая интерпретация процесса оптимизации 6.2 Получение математической модели На данном рисунке фрагмент поверхности отклика имеет
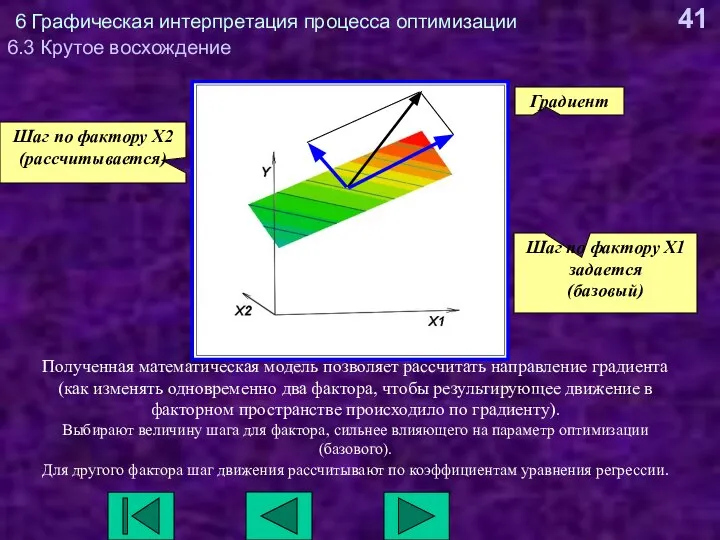
- 41. 6 Графическая интерпретация процесса оптимизации 6.3 Крутое восхождение Полученная математическая модель позволяет рассчитать направление градиента (как
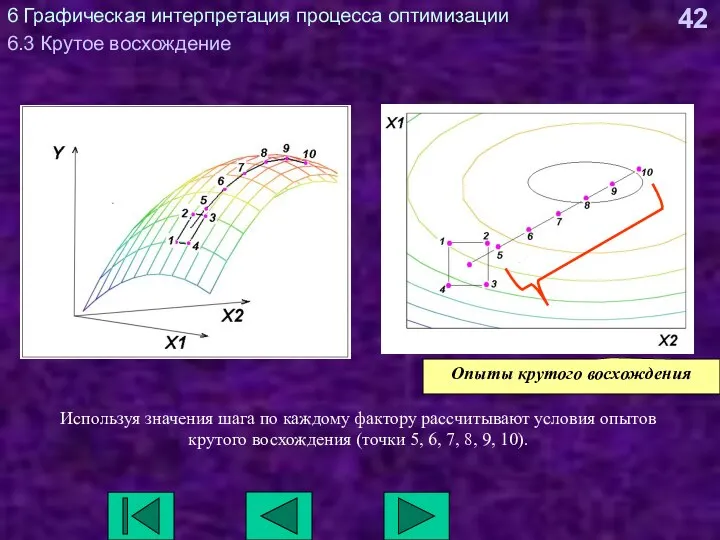
- 42. 6 Графическая интерпретация процесса оптимизации 6.3 Крутое восхождение Используя значения шага по каждому фактору рассчитывают условия
- 43. 6 Графическая интерпретация процесса оптимизации 6.3 Крутое восхождение Выполняют опыты в условиях, соответствующих точкам 5, 6,
- 44. 6 Графическая интерпретация процесса оптимизации 6.4 Уточнение положения экстремума Для проверки истинности достигнутого экстремума точку, в
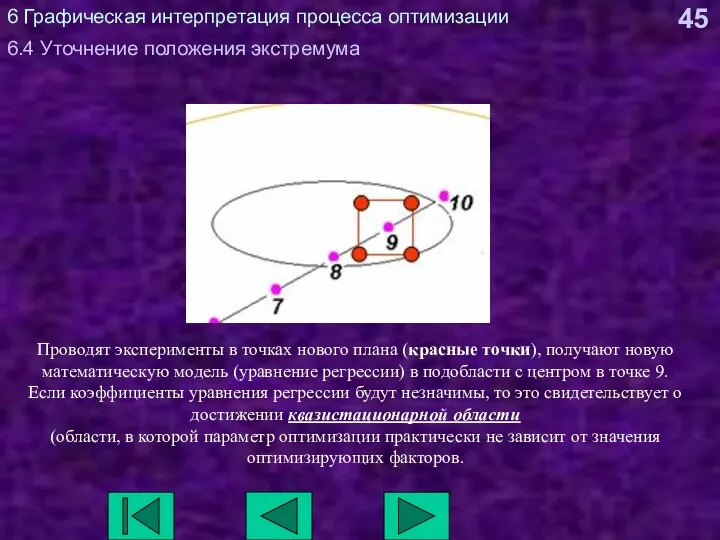
- 45. 6 Графическая интерпретация процесса оптимизации 6.4 Уточнение положения экстремума Проводят эксперименты в точках нового плана (красные
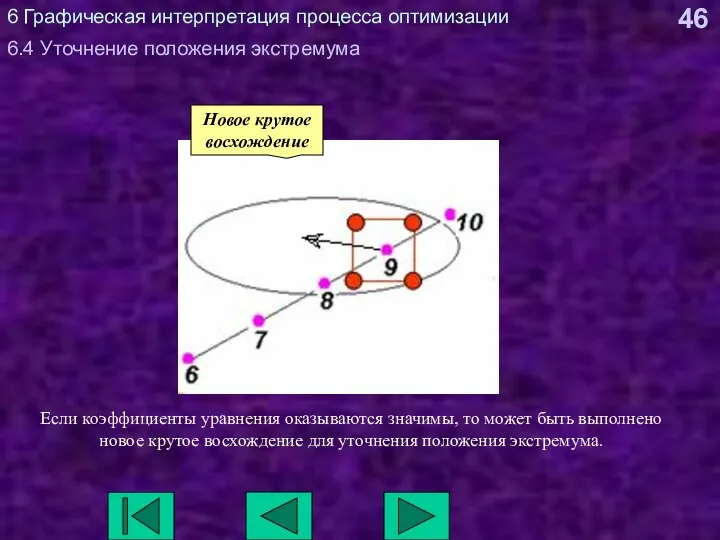
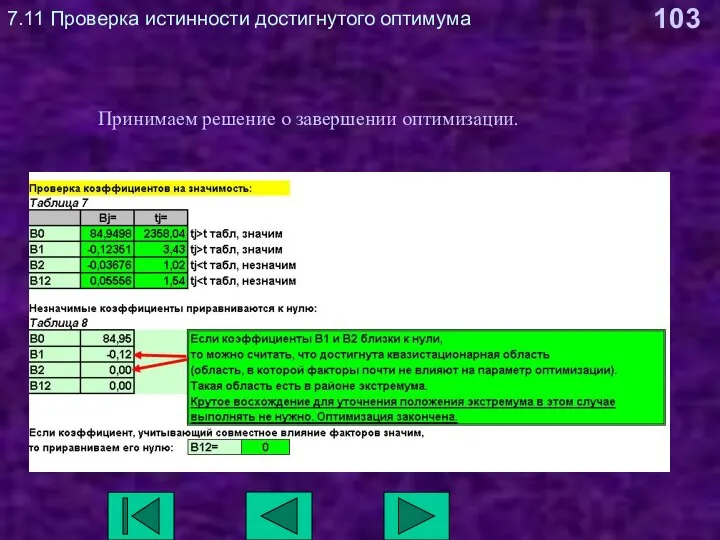
- 46. 6 Графическая интерпретация процесса оптимизации 6.4 Уточнение положения экстремума Если коэффициенты уравнения оказываются значимы, то может
- 47. Упражнение 2. Выполнение оптимизации условного технологического процесса по Боксу-Уилсону (полнофакторный эксперимент 22) с применением имитационно-моделирующей программы-тренажера.
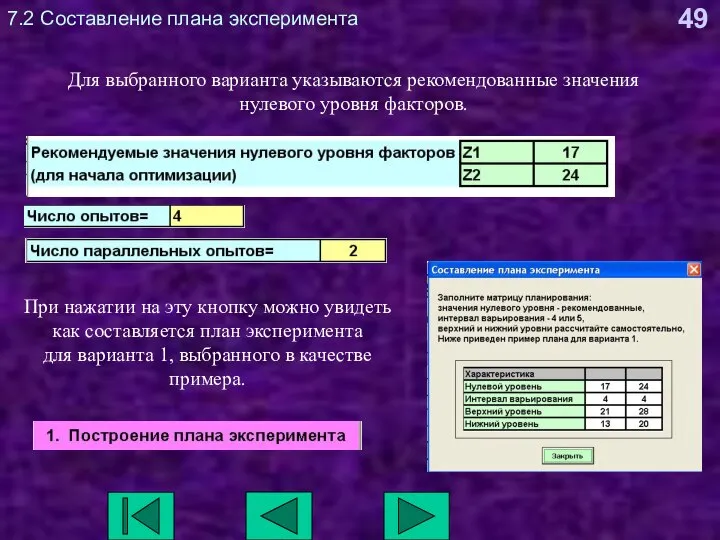
- 48. 7.1 Выбор номера варианта Запустите программу «Метод Бокса-Уилсона» Введите номер указанного преподавателем варианта.
- 49. 7.2 Составление плана эксперимента Для выбранного варианта указываются рекомендованные значения нулевого уровня факторов. При нажатии на
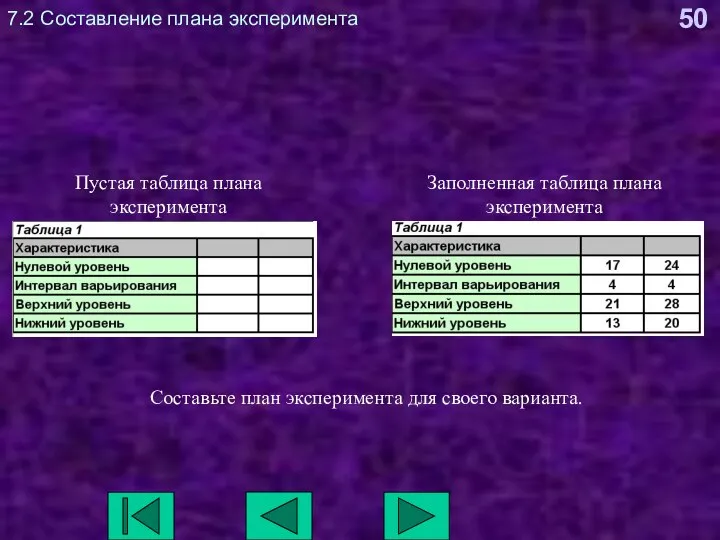
- 50. 7.2 Составление плана эксперимента Пустая таблица плана эксперимента Заполненная таблица плана эксперимента Составьте план эксперимента для
- 51. 7.2 Составление плана эксперимента На рисунке справа приведено графическое представление плана эксперимента 22.
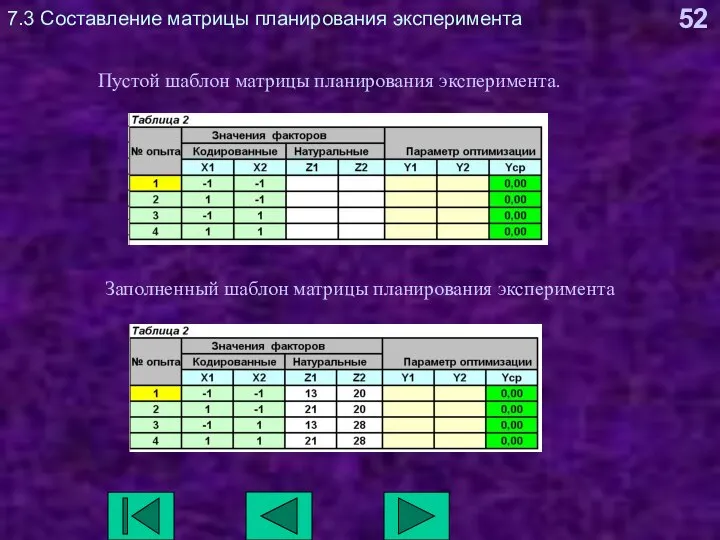
- 52. 7.3 Составление матрицы планирования эксперимента Пустой шаблон матрицы планирования эксперимента. Заполненный шаблон матрицы планирования эксперимента
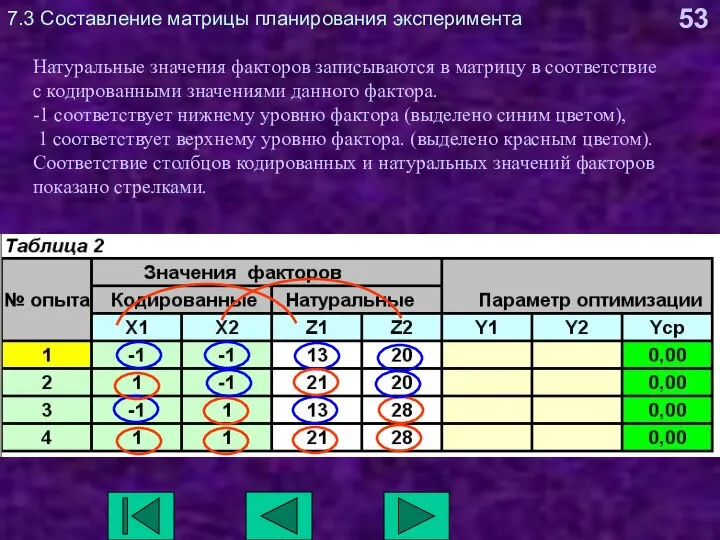
- 53. 7.3 Составление матрицы планирования эксперимента Натуральные значения факторов записываются в матрицу в соответствие с кодированными значениями
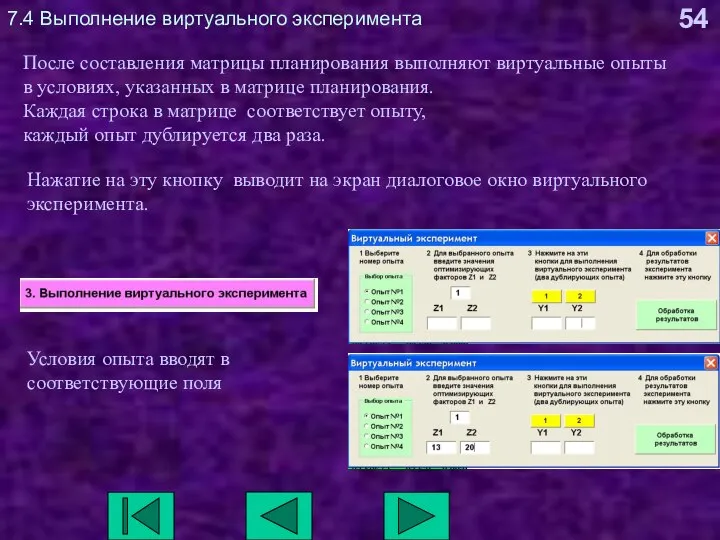
- 54. 7.4 Выполнение виртуального эксперимента После составления матрицы планирования выполняют виртуальные опыты в условиях, указанных в матрице
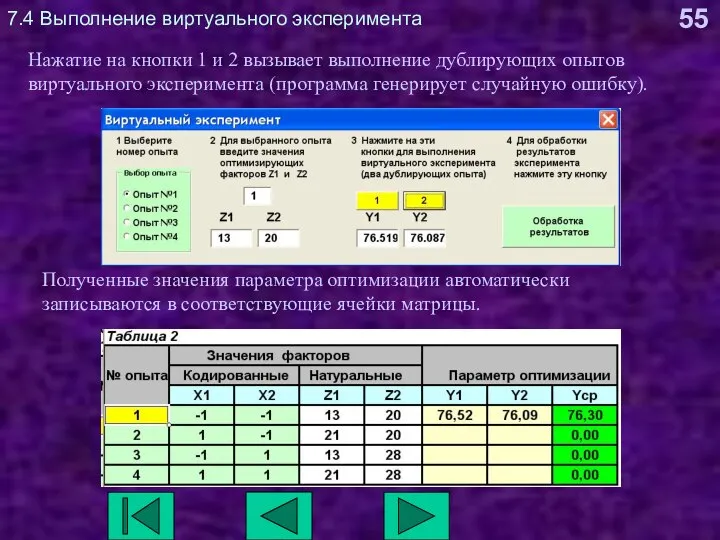
- 55. 7.4 Выполнение виртуального эксперимента Нажатие на кнопки 1 и 2 вызывает выполнение дублирующих опытов виртуального эксперимента
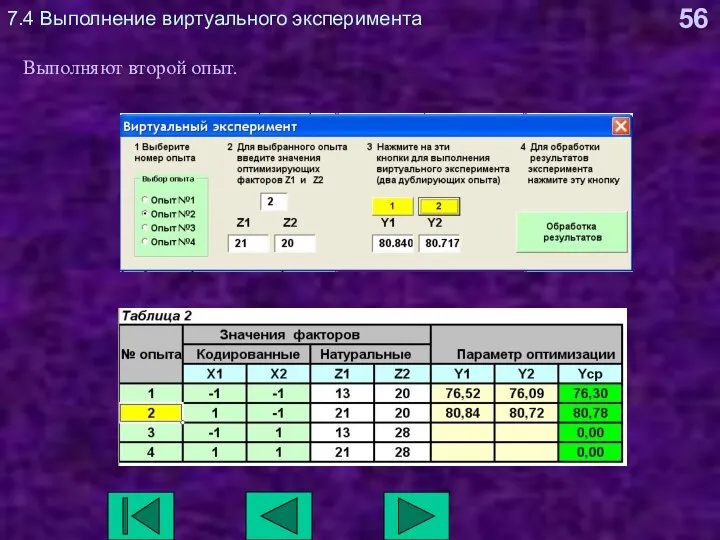
- 56. 7.4 Выполнение виртуального эксперимента Выполняют второй опыт.
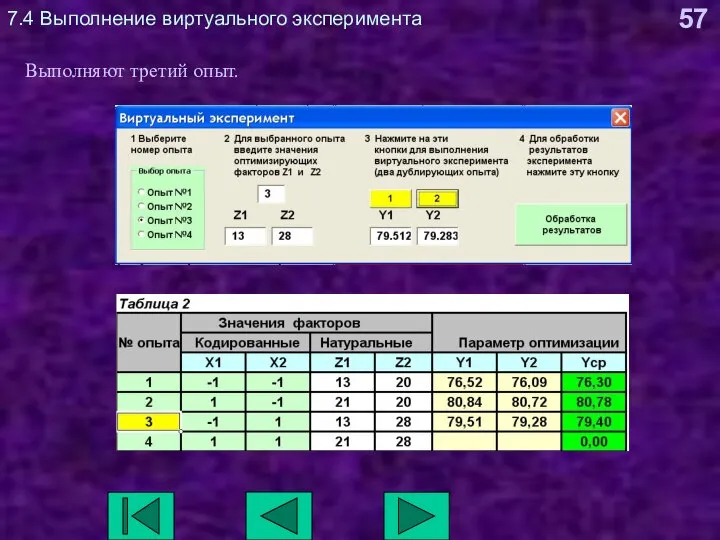
- 57. 7.4 Выполнение виртуального эксперимента Выполняют третий опыт.
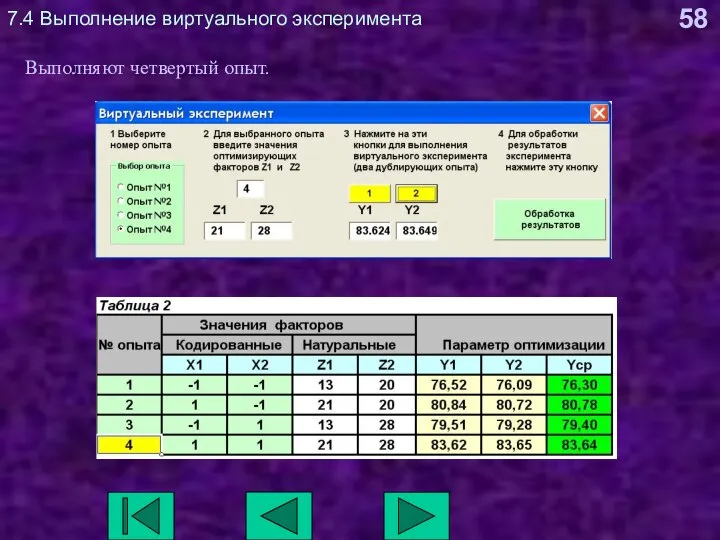
- 58. 7.4 Выполнение виртуального эксперимента Выполняют четвертый опыт.
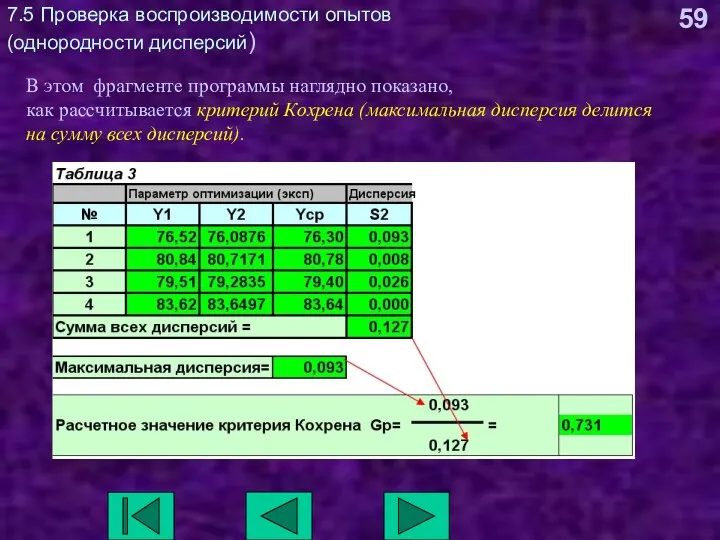
- 59. 7.5 Проверка воспроизводимости опытов (однородности дисперсий) В этом фрагменте программы наглядно показано, как рассчитывается критерий Кохрена
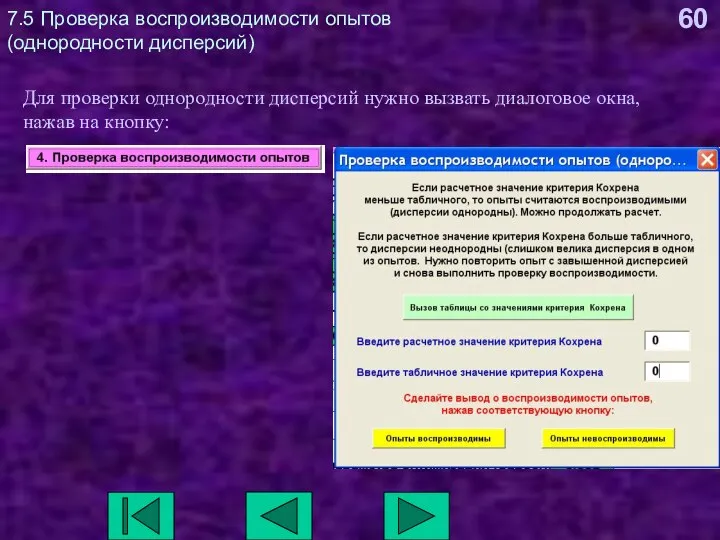
- 60. 7.5 Проверка воспроизводимости опытов (однородности дисперсий) Для проверки однородности дисперсий нужно вызвать диалоговое окна, нажав на
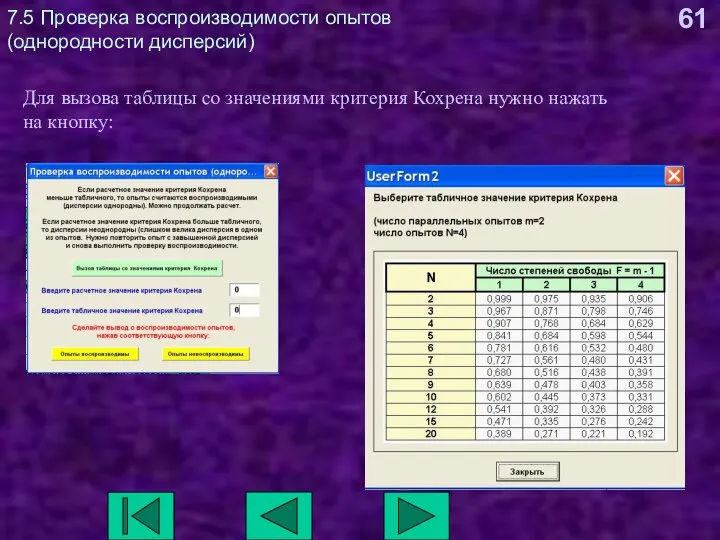
- 61. 7.5 Проверка воспроизводимости опытов (однородности дисперсий) Для вызова таблицы со значениями критерия Кохрена нужно нажать на
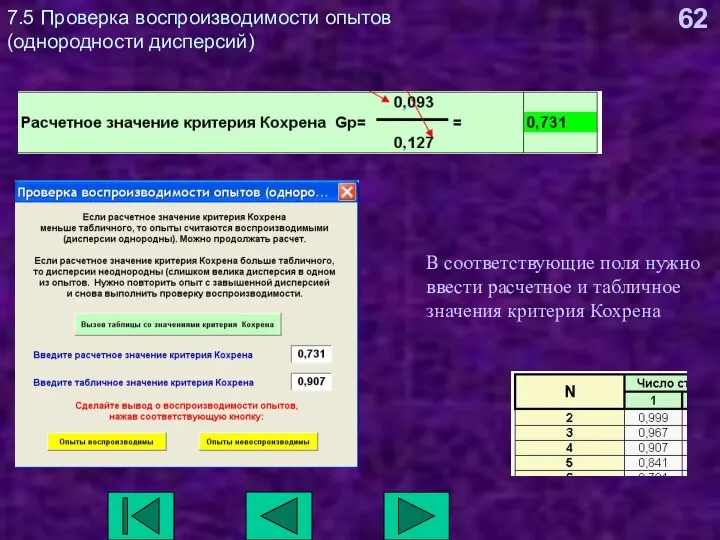
- 62. 7.5 Проверка воспроизводимости опытов (однородности дисперсий) В соответствующие поля нужно ввести расчетное и табличное значения критерия
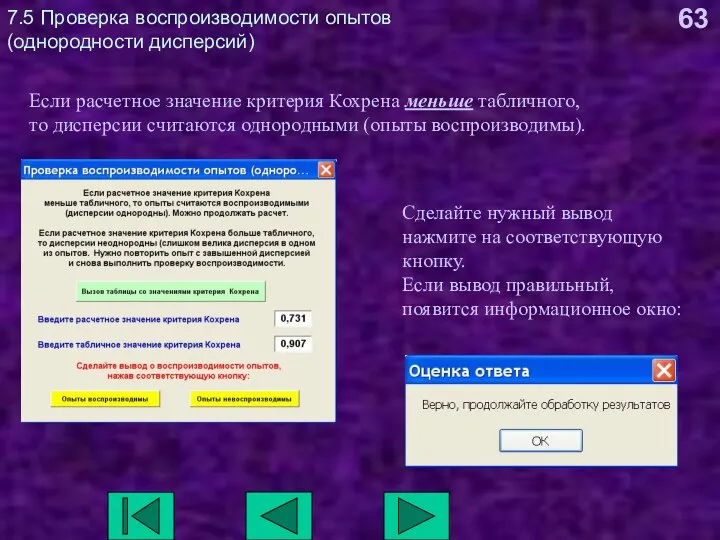
- 63. 7.5 Проверка воспроизводимости опытов (однородности дисперсий) Если расчетное значение критерия Кохрена меньше табличного, то дисперсии считаются
- 64. 7.5 Проверка воспроизводимости опытов (однородности дисперсий) Если расчетное значение критерия Кохрена больше табличного, то дисперсии считаются
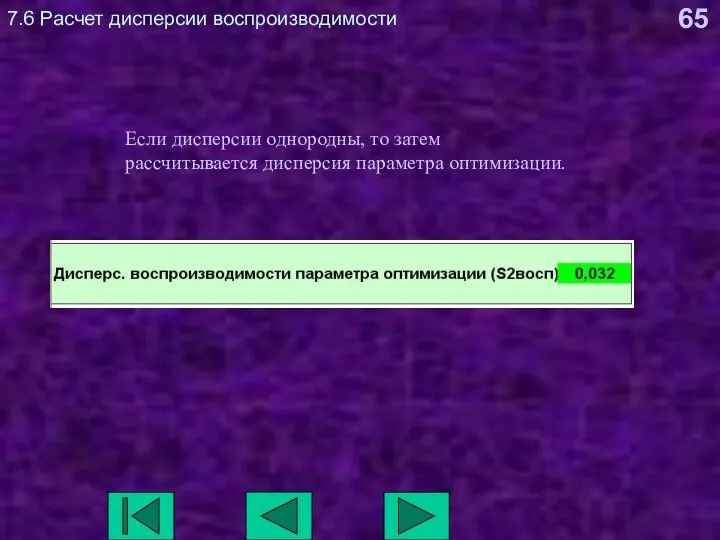
- 65. 7.6 Расчет дисперсии воспроизводимости Если дисперсии однородны, то затем рассчитывается дисперсия параметра оптимизации.
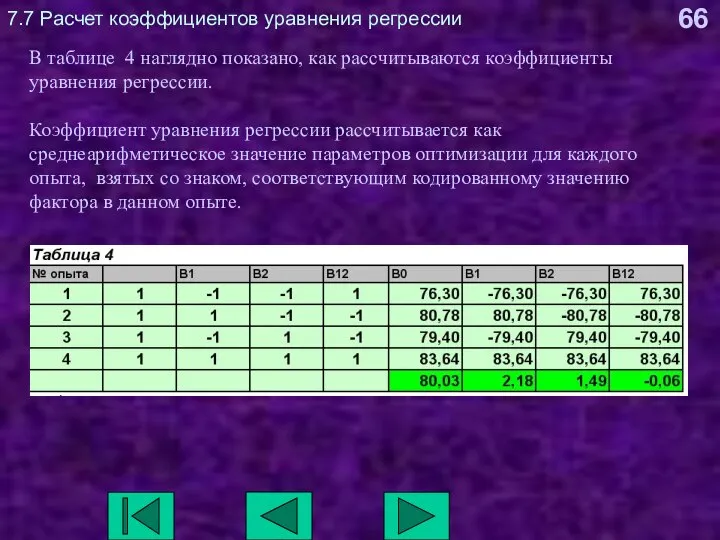
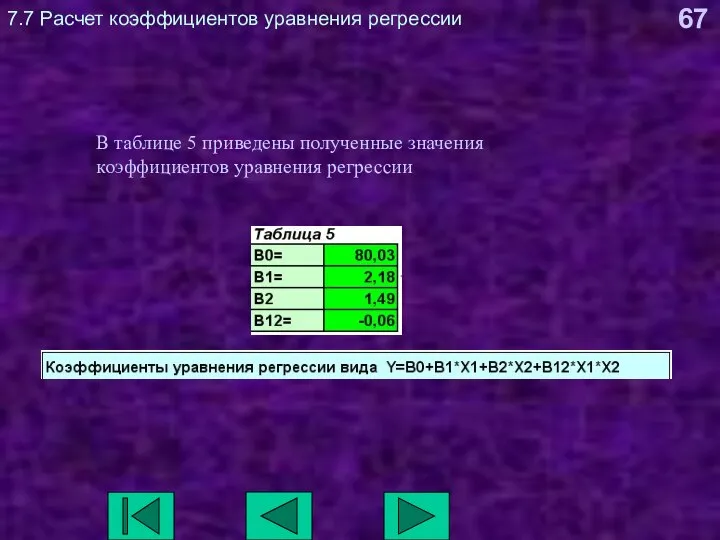
- 66. 7.7 Расчет коэффициентов уравнения регрессии В таблице 4 наглядно показано, как рассчитываются коэффициенты уравнения регрессии. Коэффициент
- 67. 7.7 Расчет коэффициентов уравнения регрессии В таблице 5 приведены полученные значения коэффициентов уравнения регрессии
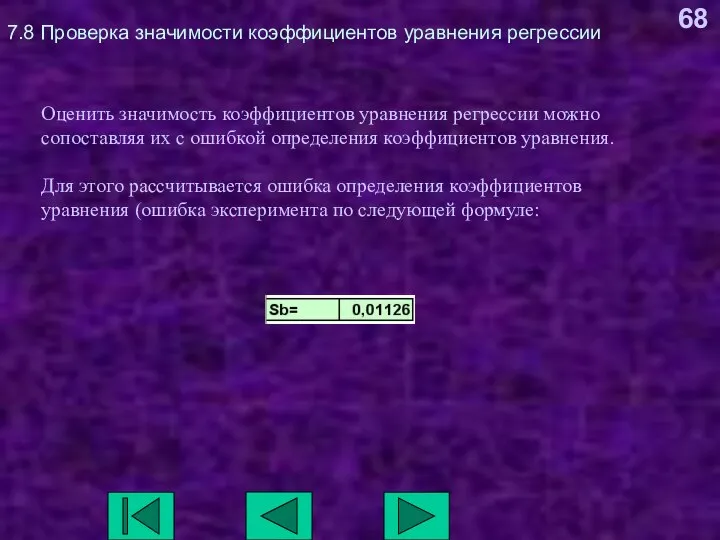
- 68. 7.8 Проверка значимости коэффициентов уравнения регрессии Оценить значимость коэффициентов уравнения регрессии можно сопоставляя их с ошибкой
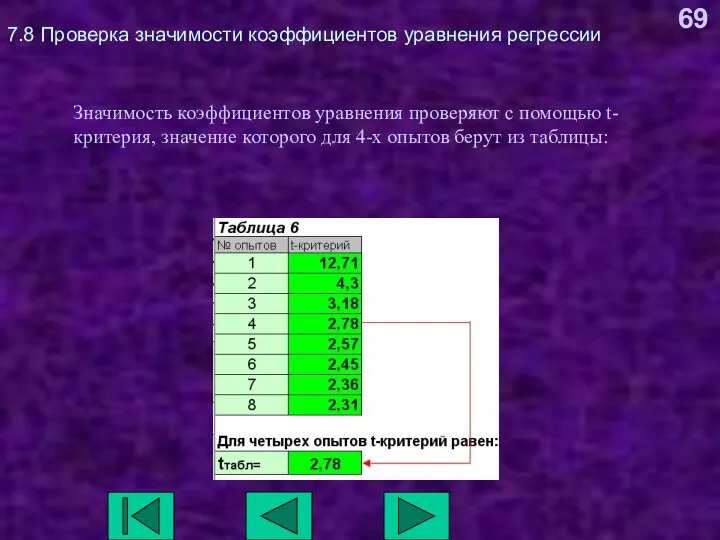
- 69. 7.8 Проверка значимости коэффициентов уравнения регрессии Значимость коэффициентов уравнения проверяют с помощью t-критерия, значение которого для
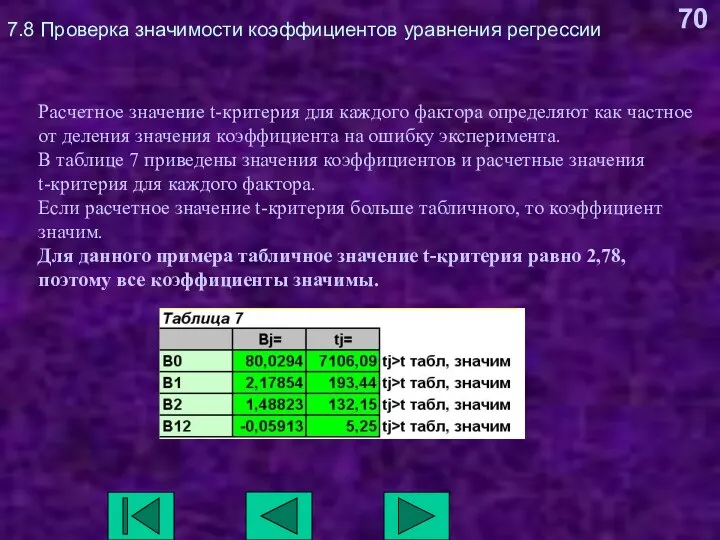
- 70. 7.8 Проверка значимости коэффициентов уравнения регрессии Расчетное значение t-критерия для каждого фактора определяют как частное от
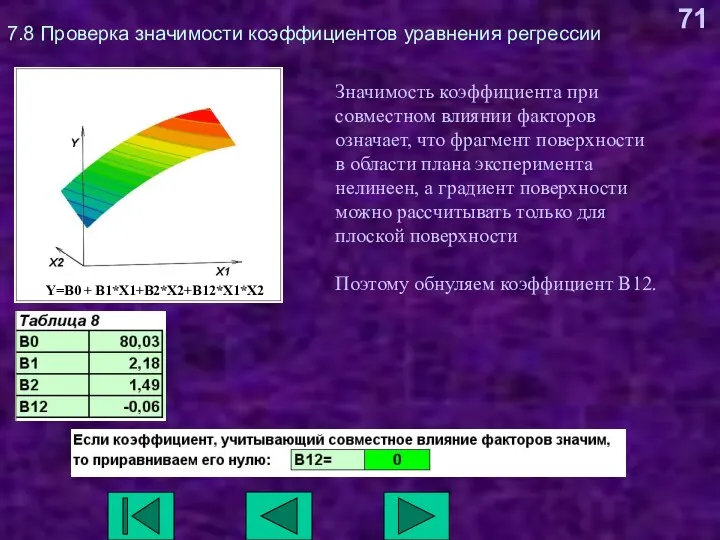
- 71. 7.8 Проверка значимости коэффициентов уравнения регрессии Y=B0 + B1*X1+B2*X2+B12*X1*X2 Значимость коэффициента при совместном влиянии факторов означает,
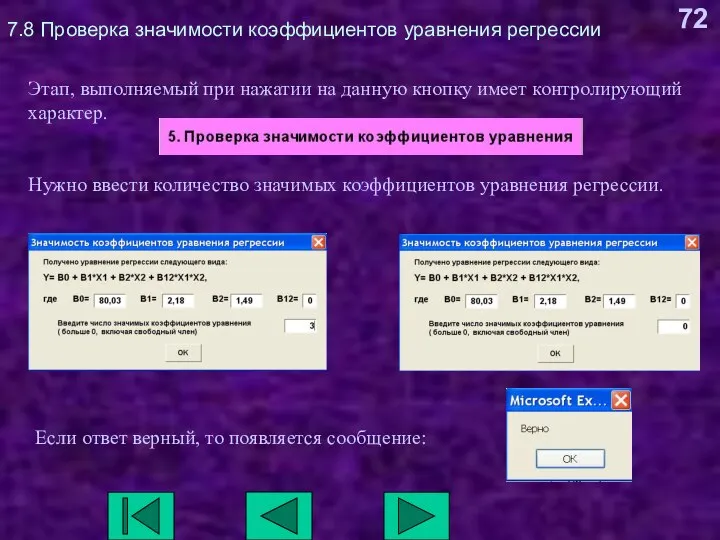
- 72. 7.8 Проверка значимости коэффициентов уравнения регрессии Этап, выполняемый при нажатии на данную кнопку имеет контролирующий характер.
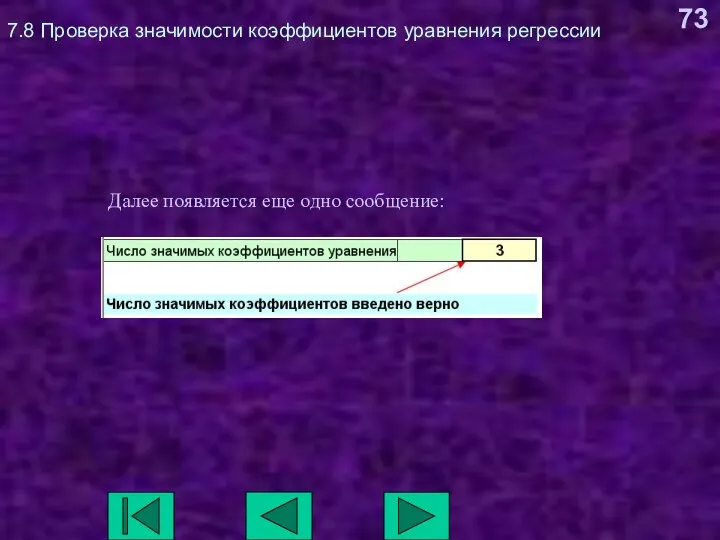
- 73. 7.8 Проверка значимости коэффициентов уравнения регрессии Далее появляется еще одно сообщение:
- 74. 7.9 Проверка адекватности уравнения регрессии Так как в уравнении регрессии теперь отсутствует член, учитывающий совместное влияние
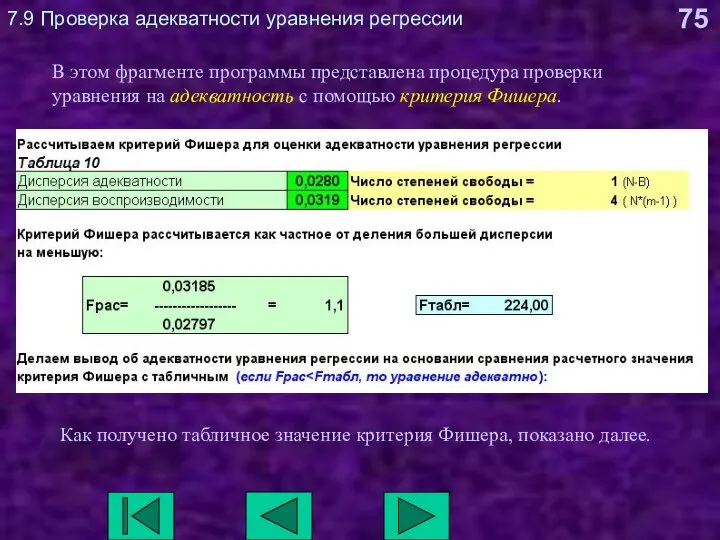
- 75. 7.9 Проверка адекватности уравнения регрессии В этом фрагменте программы представлена процедура проверки уравнения на адекватность с
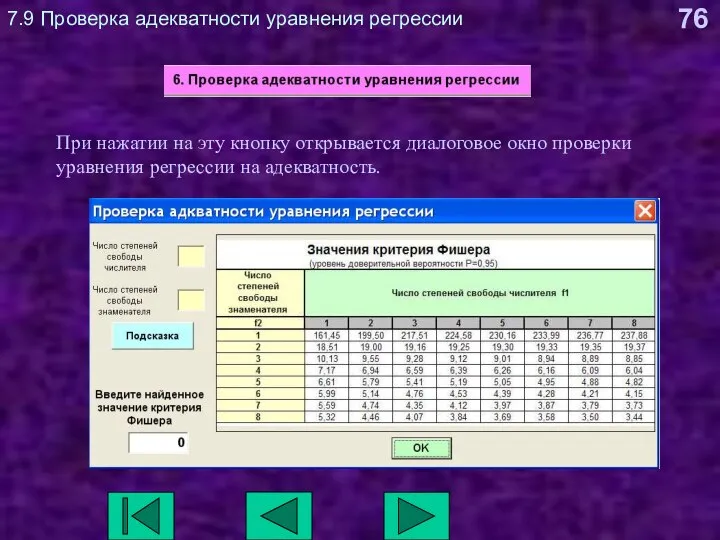
- 76. 7.9 Проверка адекватности уравнения регрессии При нажатии на эту кнопку открывается диалоговое окно проверки уравнения регрессии
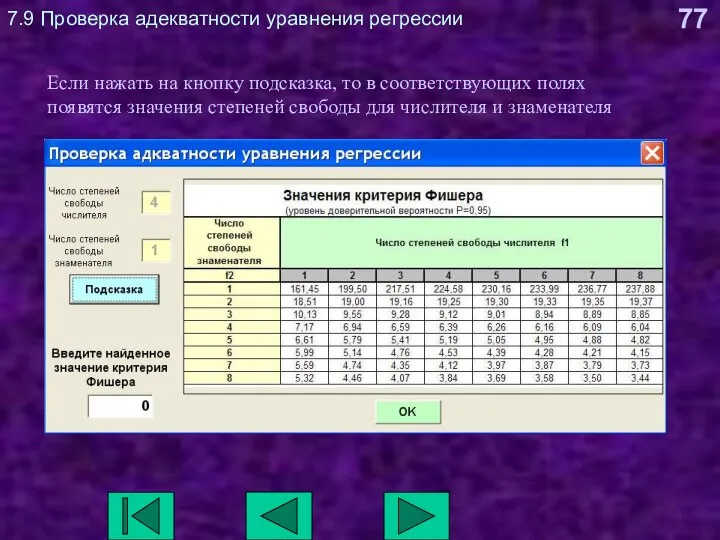
- 77. 7.9 Проверка адекватности уравнения регрессии Если нажать на кнопку подсказка, то в соответствующих полях появятся значения
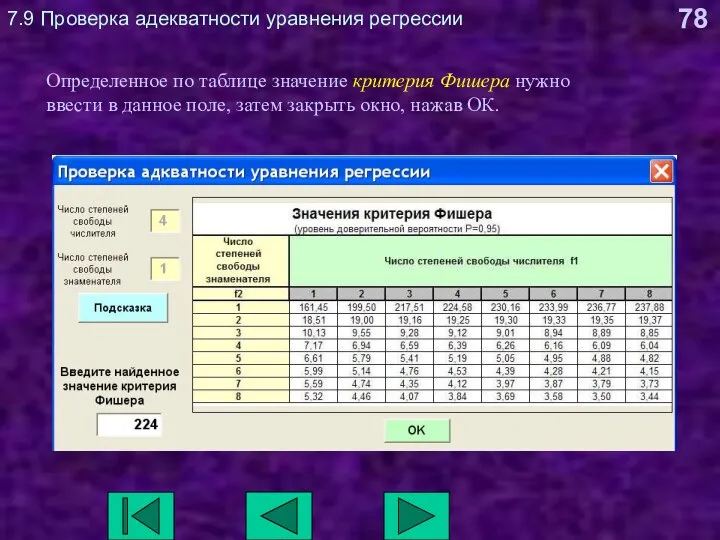
- 78. 7.9 Проверка адекватности уравнения регрессии Определенное по таблице значение критерия Фишера нужно ввести в данное поле,
- 79. 7.9 Проверка адекватности уравнения регрессии Если расчетное значение критерия Фишера меньше табличного, то уравнение адекватно. В
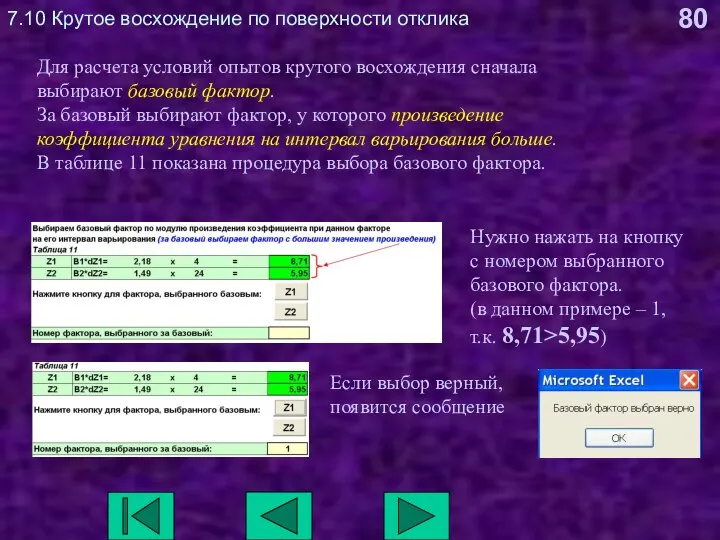
- 80. 7.10 Крутое восхождение по поверхности отклика Для расчета условий опытов крутого восхождения сначала выбирают базовый фактор.
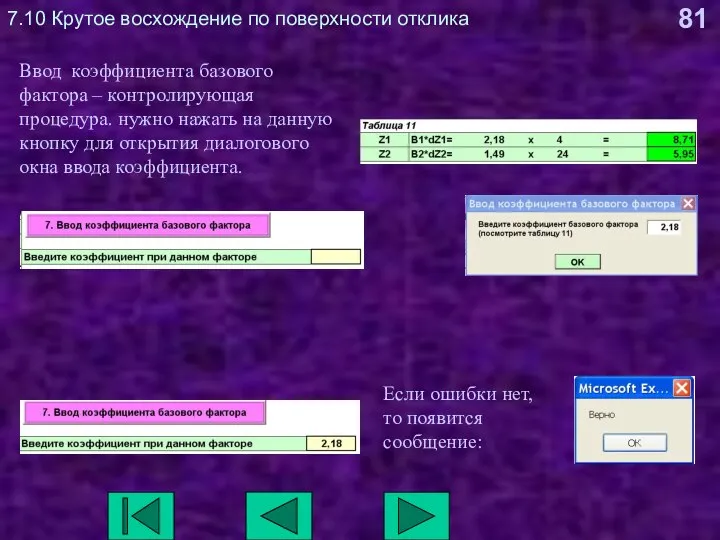
- 81. 7.10 Крутое восхождение по поверхности отклика Ввод коэффициента базового фактора – контролирующая процедура. нужно нажать на
- 82. 7.10 Крутое восхождение по поверхности отклика Математическая модель (уравнение регрессии) фрагмента поверхности отклика (квадрат с вершинами
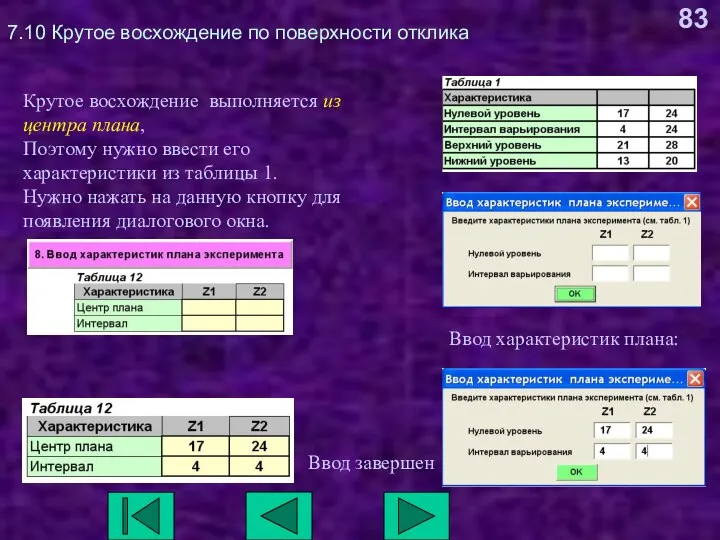
- 83. 7.10 Крутое восхождение по поверхности отклика Крутое восхождение выполняется из центра плана, Поэтому нужно ввести его
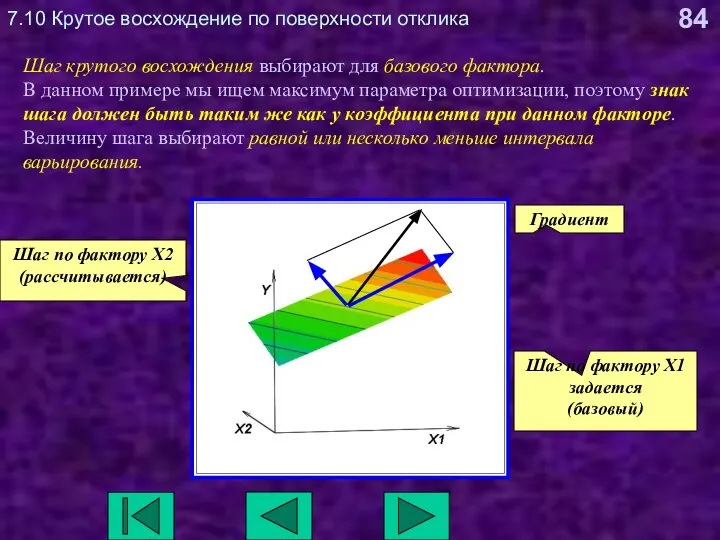
- 84. 7.10 Крутое восхождение по поверхности отклика Шаг крутого восхождения выбирают для базового фактора. В данном примере
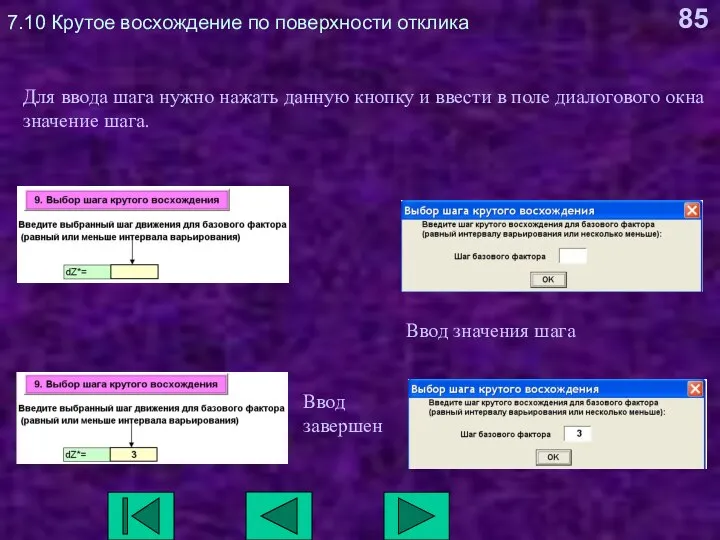
- 85. 7.10 Крутое восхождение по поверхности отклика Для ввода шага нужно нажать данную кнопку и ввести в
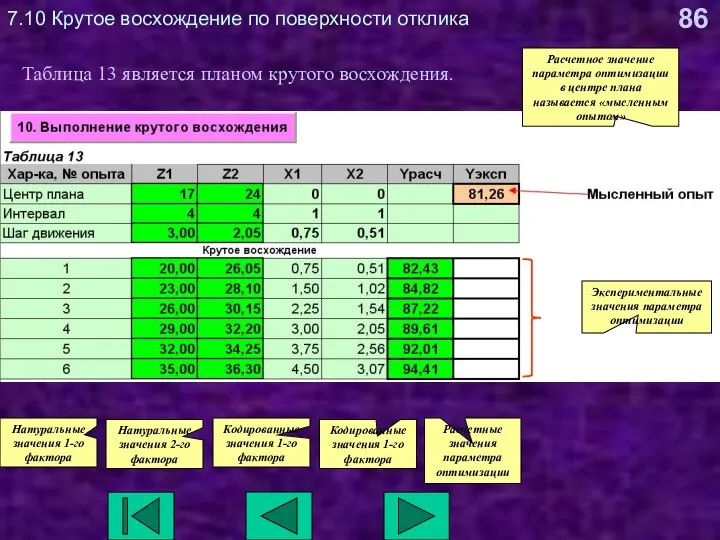
- 86. 7.10 Крутое восхождение по поверхности отклика Таблица 13 является планом крутого восхождения. Натуральные значения 1-го фактора
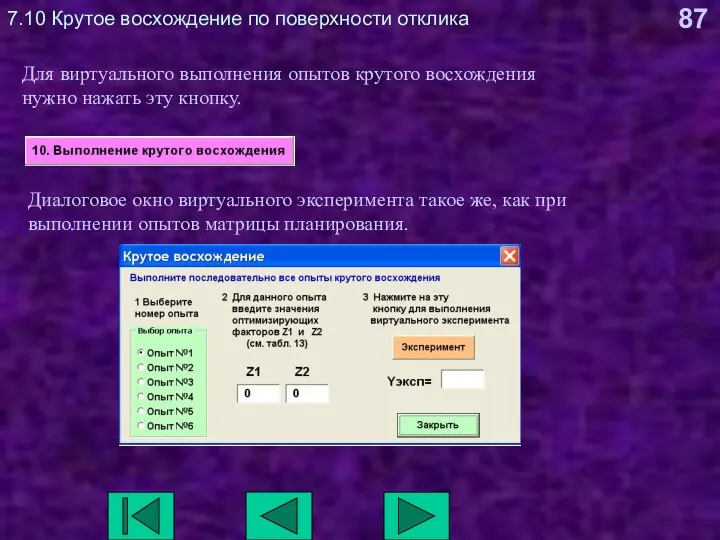
- 87. 7.10 Крутое восхождение по поверхности отклика Для виртуального выполнения опытов крутого восхождения нужно нажать эту кнопку.
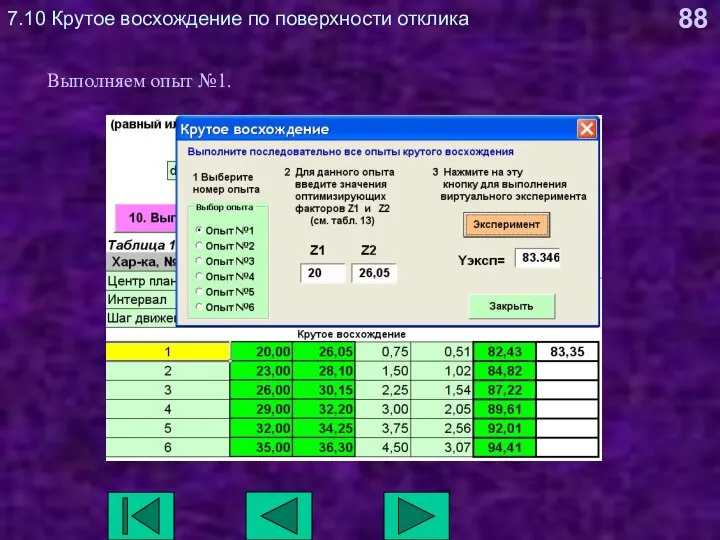
- 88. 7.10 Крутое восхождение по поверхности отклика Выполняем опыт №1.
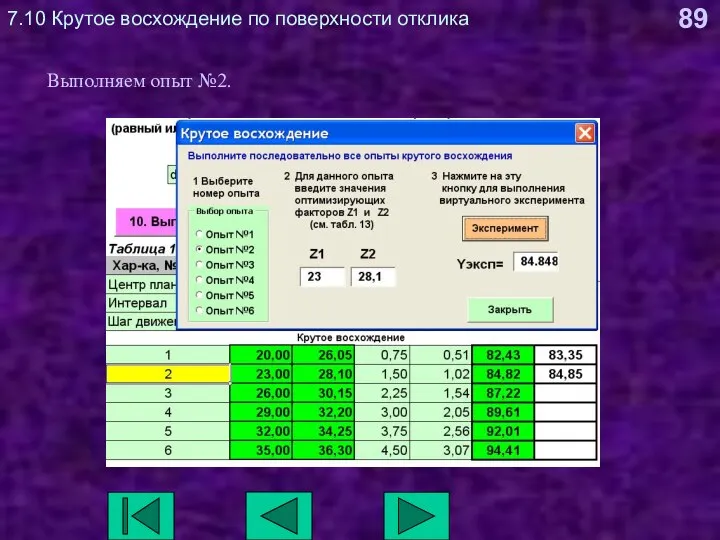
- 89. 7.10 Крутое восхождение по поверхности отклика Выполняем опыт №2.
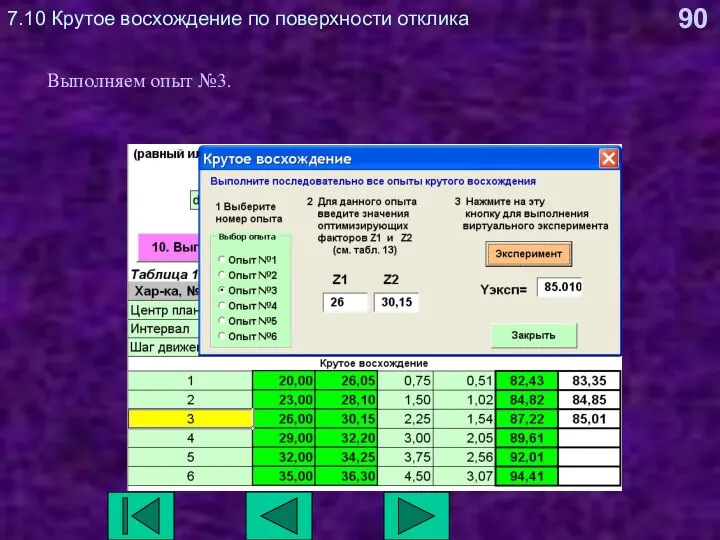
- 90. 7.10 Крутое восхождение по поверхности отклика Выполняем опыт №3.
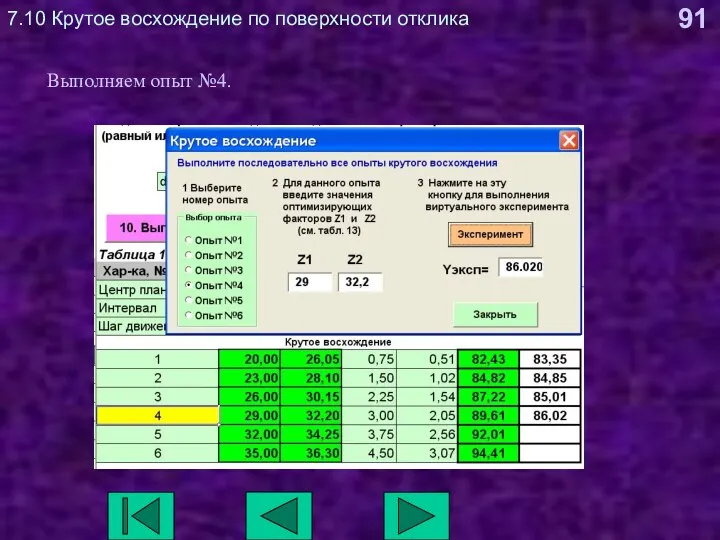
- 91. 7.10 Крутое восхождение по поверхности отклика Выполняем опыт №4.
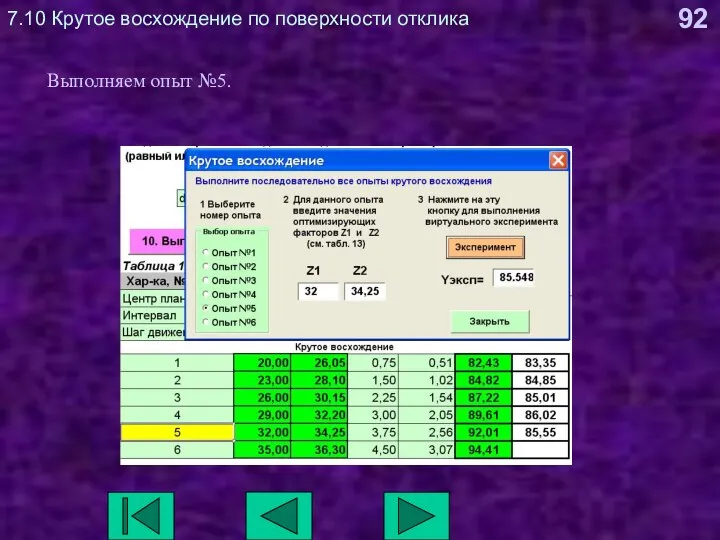
- 92. 7.10 Крутое восхождение по поверхности отклика Выполняем опыт №5.
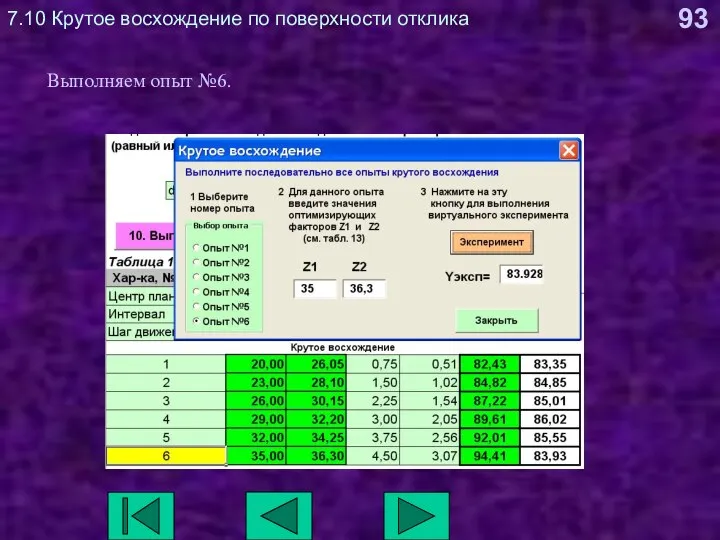
- 93. 7.10 Крутое восхождение по поверхности отклика Выполняем опыт №6.
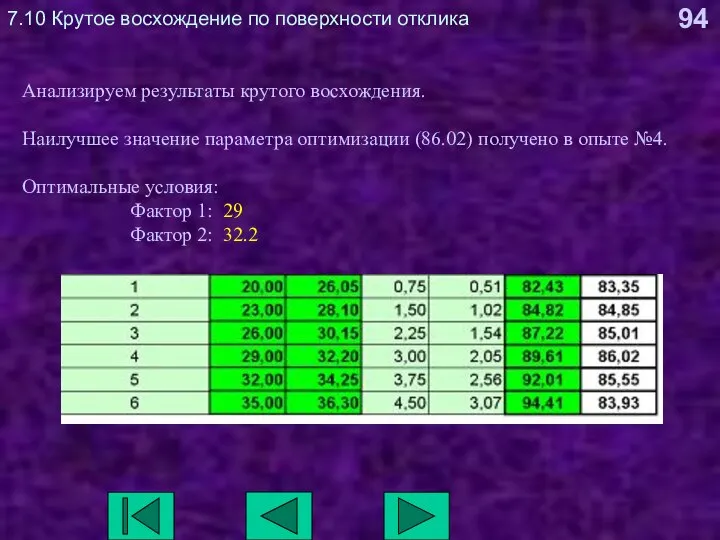
- 94. 7.10 Крутое восхождение по поверхности отклика Анализируем результаты крутого восхождения. Наилучшее значение параметра оптимизации (86.02) получено
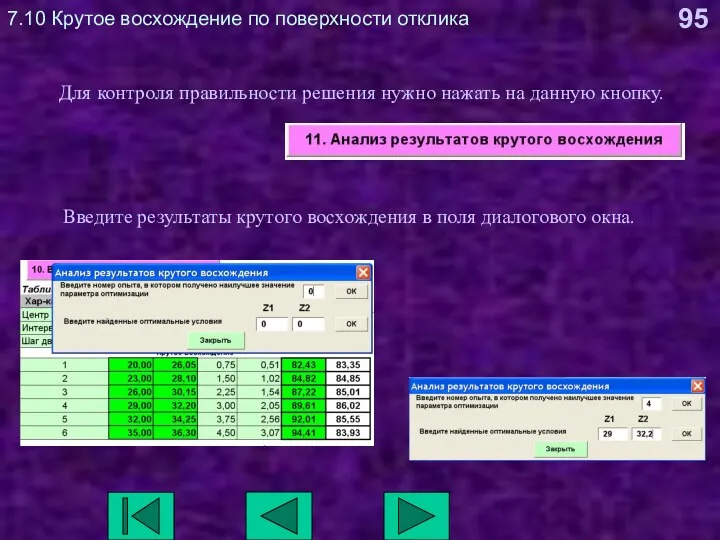
- 95. 7.10 Крутое восхождение по поверхности отклика Для контроля правильности решения нужно нажать на данную кнопку. Введите
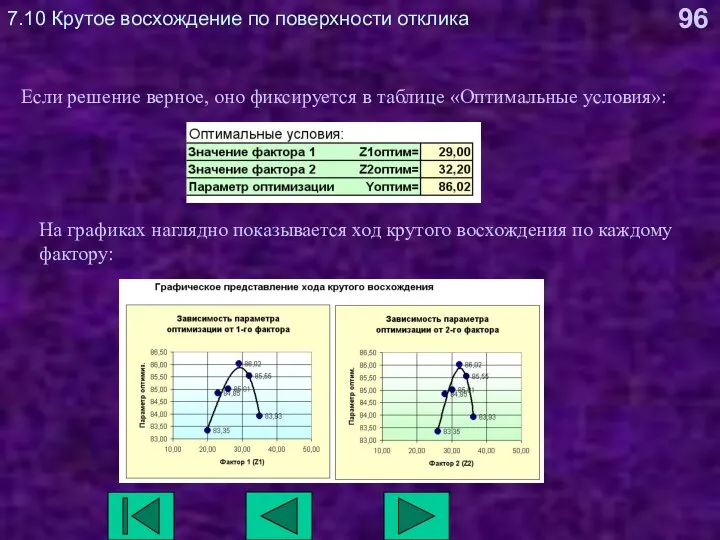
- 96. 7.10 Крутое восхождение по поверхности отклика Если решение верное, оно фиксируется в таблице «Оптимальные условия»: На
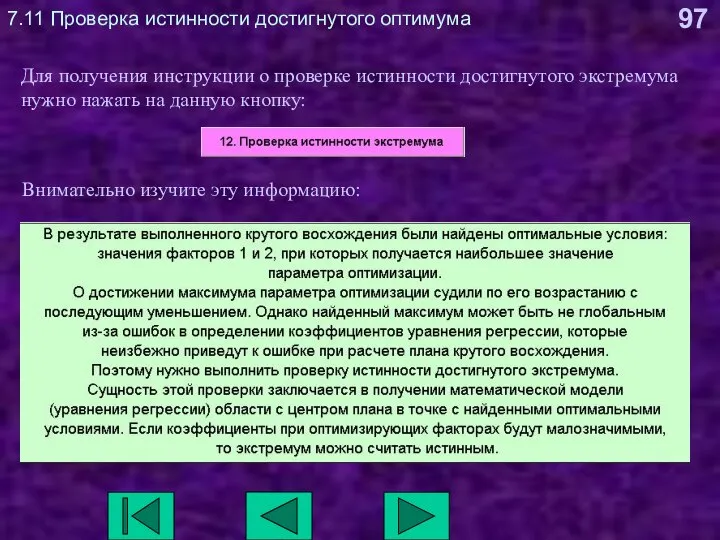
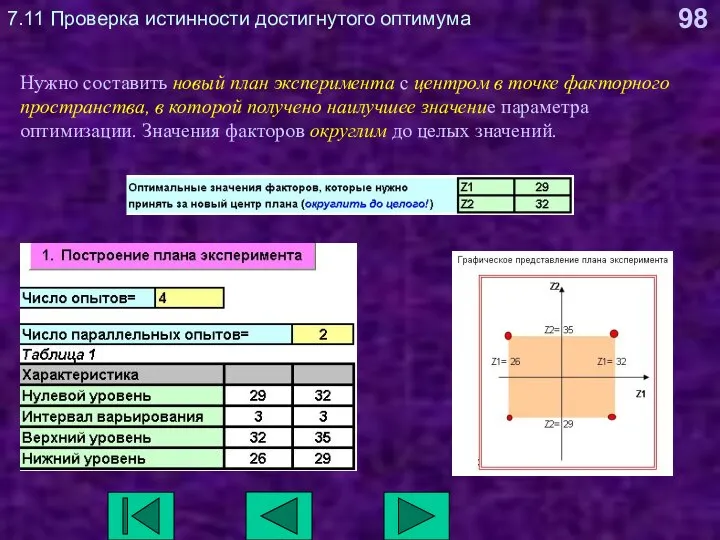
- 97. 7.11 Проверка истинности достигнутого оптимума Для получения инструкции о проверке истинности достигнутого экстремума нужно нажать на
- 98. 7.11 Проверка истинности достигнутого оптимума Нужно составить новый план эксперимента с центром в точке факторного пространства,
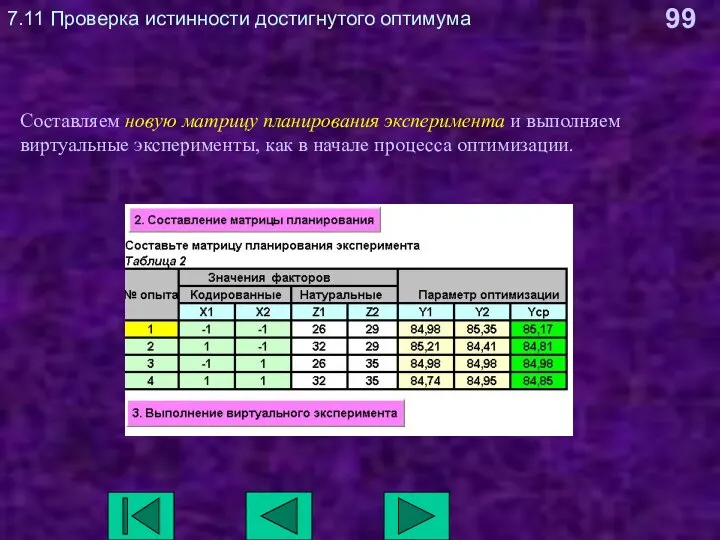
- 99. 7.11 Проверка истинности достигнутого оптимума Составляем новую матрицу планирования эксперимента и выполняем виртуальные эксперименты, как в
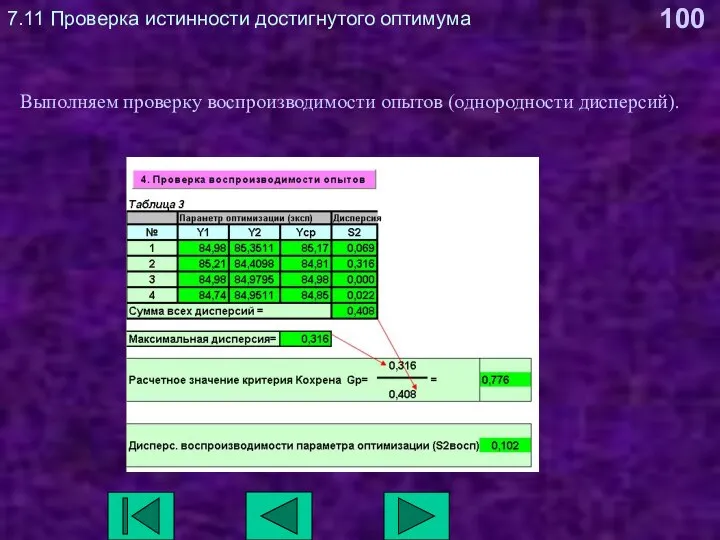
- 100. 7.11 Проверка истинности достигнутого оптимума Выполняем проверку воспроизводимости опытов (однородности дисперсий).
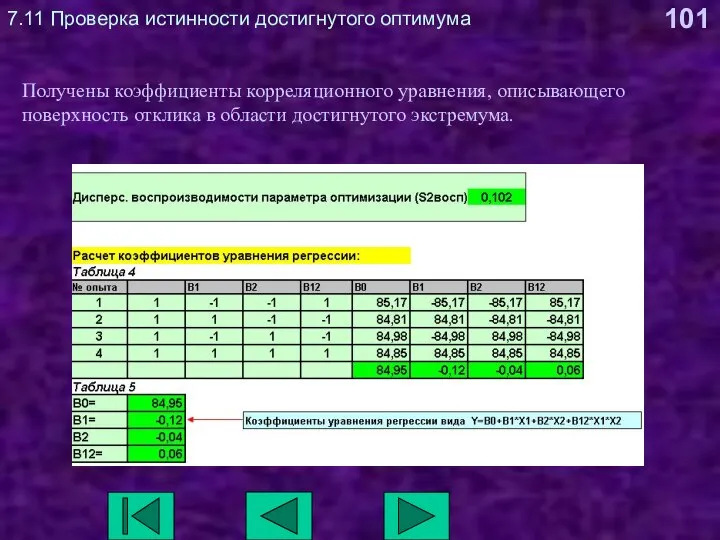
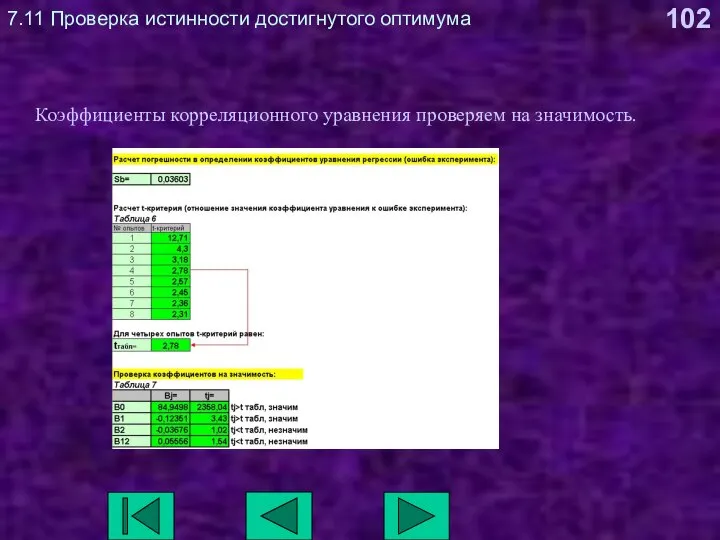
- 101. 7.11 Проверка истинности достигнутого оптимума Получены коэффициенты корреляционного уравнения, описывающего поверхность отклика в области достигнутого экстремума.
- 102. 7.11 Проверка истинности достигнутого оптимума Коэффициенты корреляционного уравнения проверяем на значимость.
- 103. 7.11 Проверка истинности достигнутого оптимума Принимаем решение о завершении оптимизации.
- 104. 7 Упражнение 2. Оптимизация по Боксу-Уилсону Для запуска программы-имитатора лабораторной работы нажмите на ссылку. При работе
- 106. Скачать презентацию




















 Одночлен и его стандартный вид
Одночлен и его стандартный вид Тригонометрические тождества. Преобразование тригонометрических выражений
Тригонометрические тождества. Преобразование тригонометрических выражений комбинаторика 1 лекция-1
комбинаторика 1 лекция-1 Определение и знаки тригонометрических функций
Определение и знаки тригонометрических функций Топология
Топология Штангенциркуль
Штангенциркуль Занимательная математика (3 класс)
Занимательная математика (3 класс) Запись Арифметических выражений и на языке программирования Паскаль
Запись Арифметических выражений и на языке программирования Паскаль Одночлены
Одночлены Числовые характеристики дискретной случайной величины (ДСВ). Математическое ожидание, мода, медиана
Числовые характеристики дискретной случайной величины (ДСВ). Математическое ожидание, мода, медиана Построение графиков тригонометрических функций
Построение графиков тригонометрических функций Презентация на тему Треугольники (5 класс)
Презентация на тему Треугольники (5 класс)  Усный счет
Усный счет Перпендикуляр и наклонная. 8 класс
Перпендикуляр и наклонная. 8 класс Узоры и орнаменты на посуде
Узоры и орнаменты на посуде Завдання на відсотки
Завдання на відсотки Сравнение десятичных дробей
Сравнение десятичных дробей Формулы сокращённого умножения
Формулы сокращённого умножения Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Свойства точек числовой окружности
Свойства точек числовой окружности Решение задач с помощью систем уравнений (часть 2)
Решение задач с помощью систем уравнений (часть 2) Модуль числа. 6 класс
Модуль числа. 6 класс Деление десятичной дроби на натуральное число. Графический диктант
Деление десятичной дроби на натуральное число. Графический диктант Osnovnoe_svoystvo_drobi (1)
Osnovnoe_svoystvo_drobi (1) Презентация на тему Математика в профессиях (11 класс)
Презентация на тему Математика в профессиях (11 класс)  Явная разностная схема для полной системы уравнений Навье-Стокса
Явная разностная схема для полной системы уравнений Навье-Стокса Урок математики в 1 классе
Урок математики в 1 классе Статистическое изучение связей между явлениями (4 часа). Тема 1.7
Статистическое изучение связей между явлениями (4 часа). Тема 1.7