Содержание
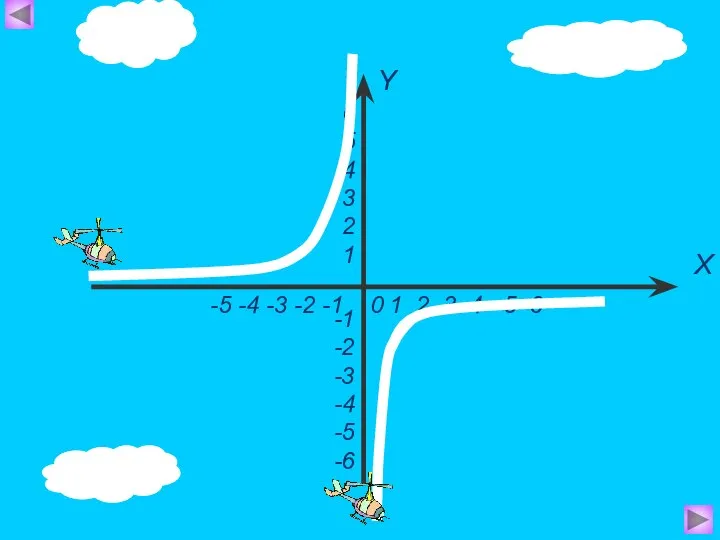
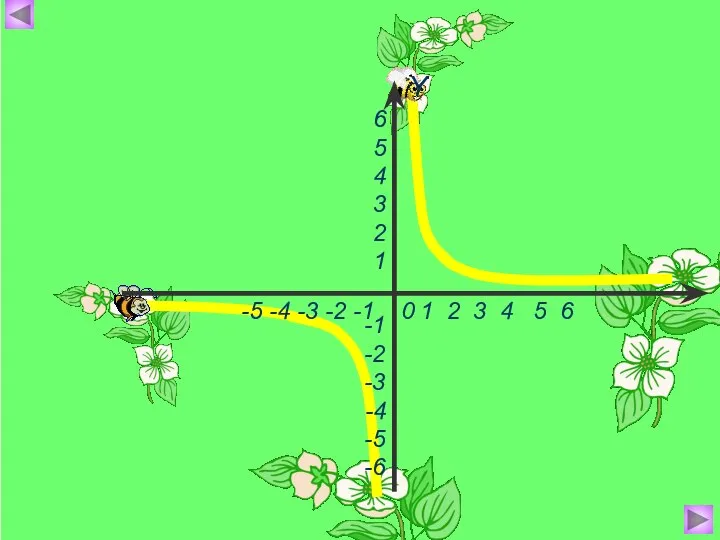
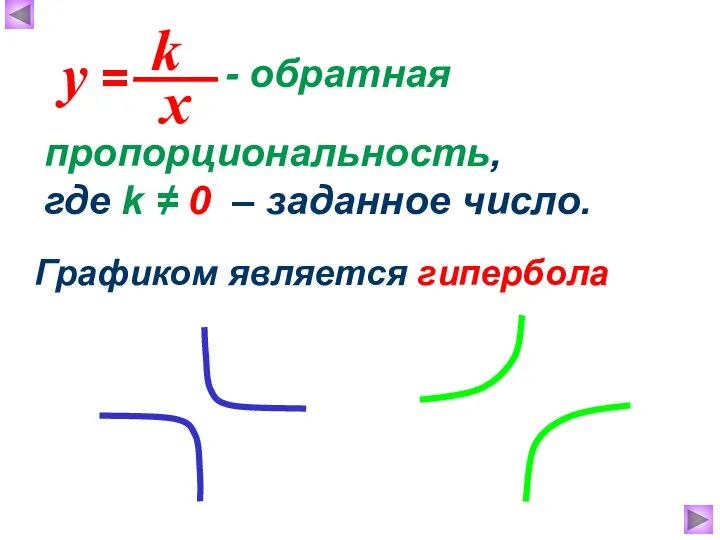
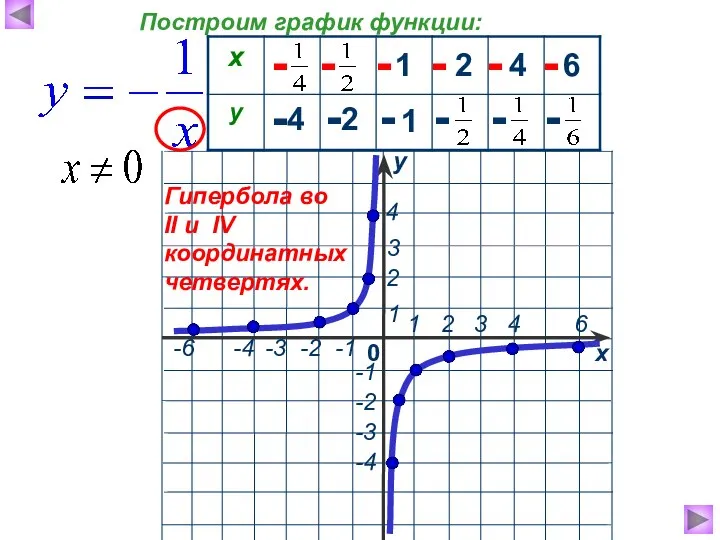
- 4. - обратная Графиком является гипербола пропорциональность, где k ≠ 0 – заданное число.
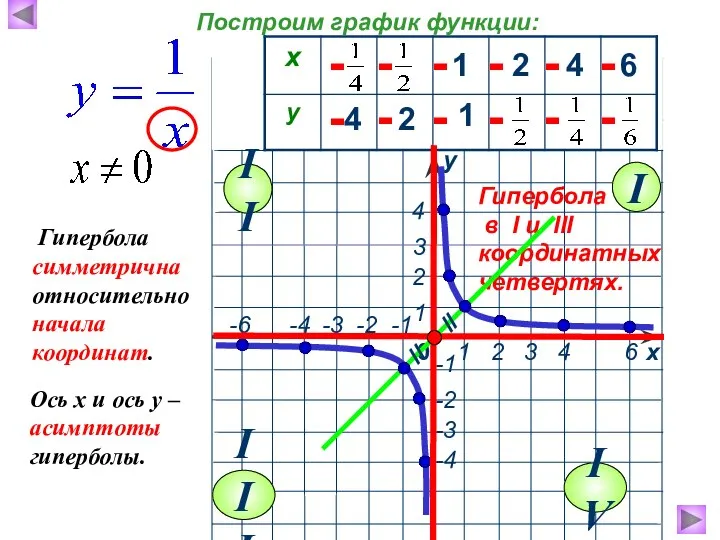
- 5. 1 2 4 6 4 2 1 - - - - - - - - -
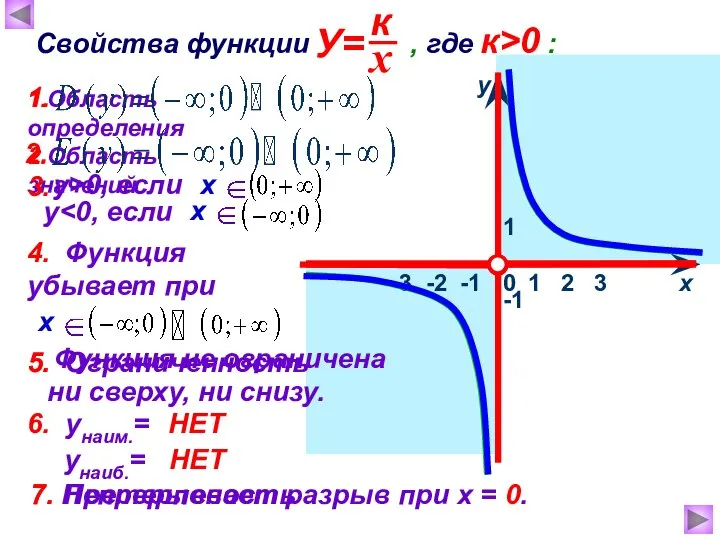
- 6. 1 х у 0 Свойства функции , где к>0 : 1.Область определения -1 2.Область значений 3.
- 7. 1 2 4 6 4 2 1 - - - - - - - - -
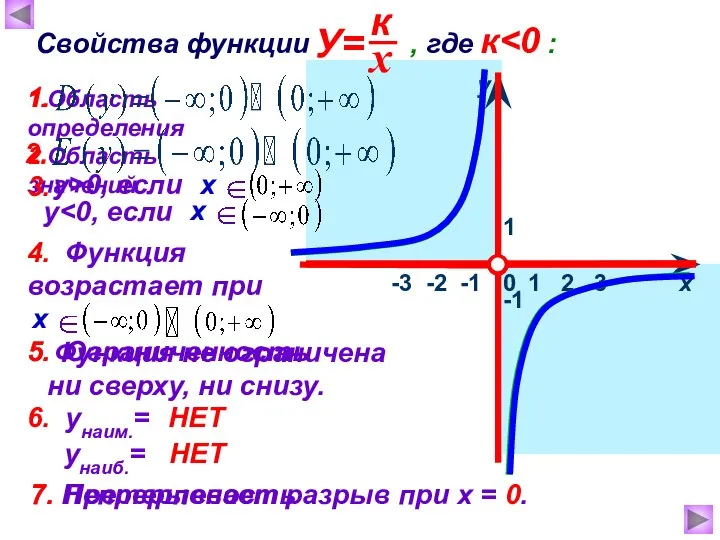
- 8. 1 х у 0 Свойства функции , где к 1.Область определения -1 2.Область значений 3. 1
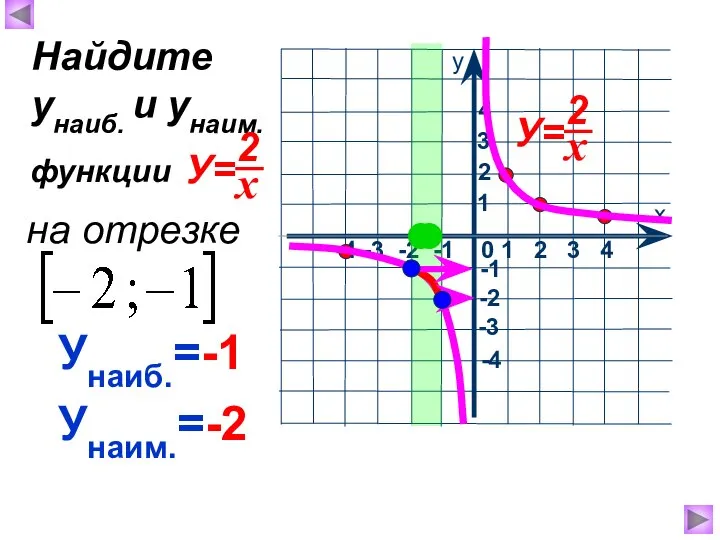
- 9. Унаиб.=-1 Унаим.=-2 Найдите унаиб. и унаим. на отрезке функции
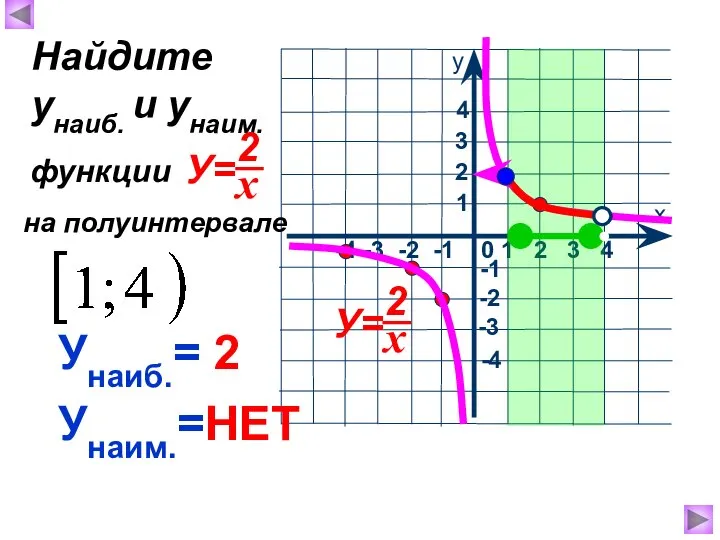
- 10. Унаиб.= 2 Унаим.=НЕТ Найдите унаиб. и унаим. на полуинтервале функции
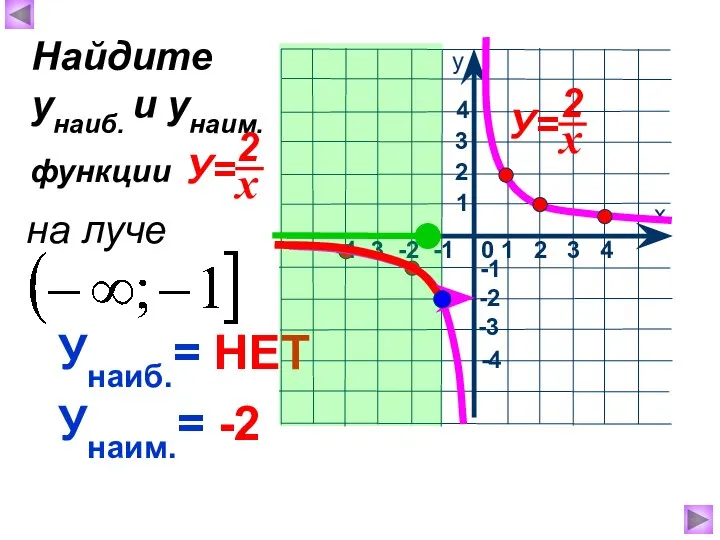
- 11. Унаиб.= НЕТ Унаим.= -2 Найдите унаиб. и унаим. функции на луче
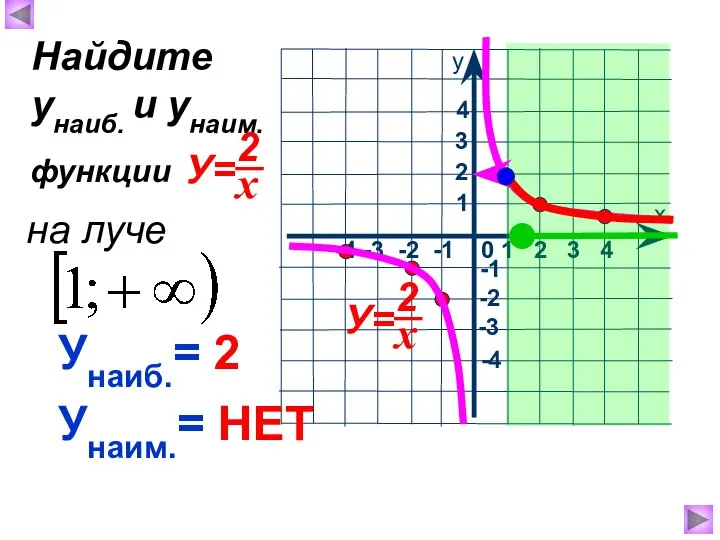
- 12. Унаиб.= 2 Унаим.= НЕТ Найдите унаиб. и унаим. функции на луче
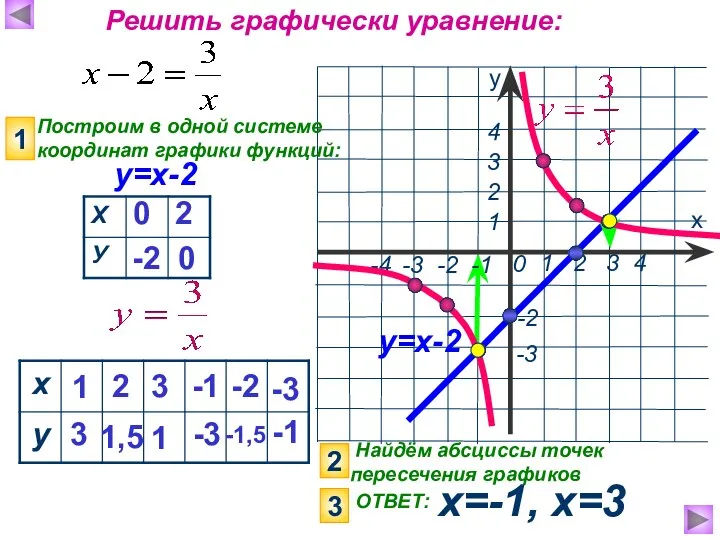
- 13. Найдём абсциссы точек пересечения графиков х=-1, х=3 х у 1 2 3 4 0 -3 1
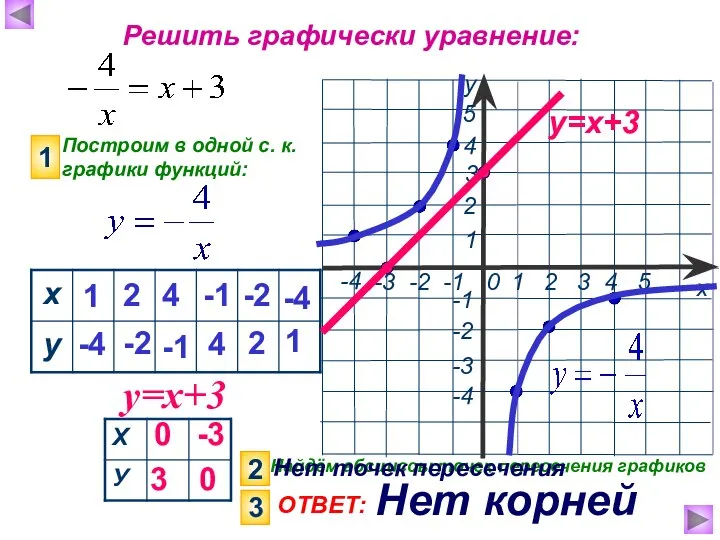
- 14. Решить графически уравнение: Построим в одной с. к. графики функций: 1 у=х+3 1 -4 2 -2
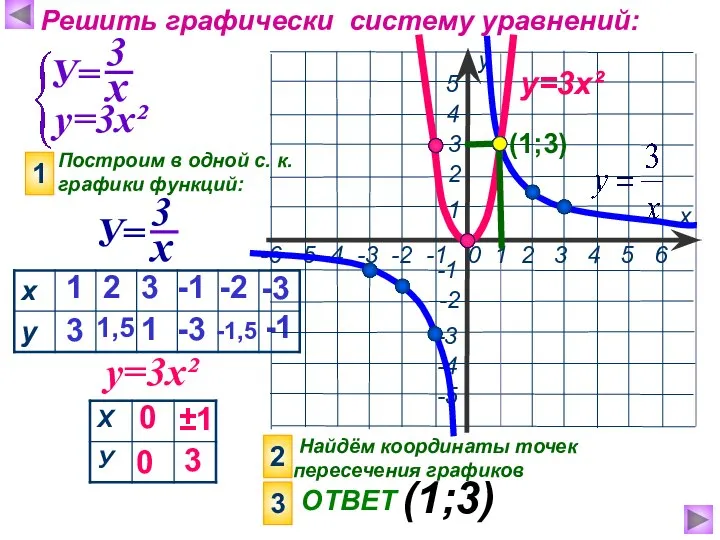
- 15. Решить графически систему уравнений: у=3х² Построим в одной с. к. графики функций: 1 у=3х² 1 3
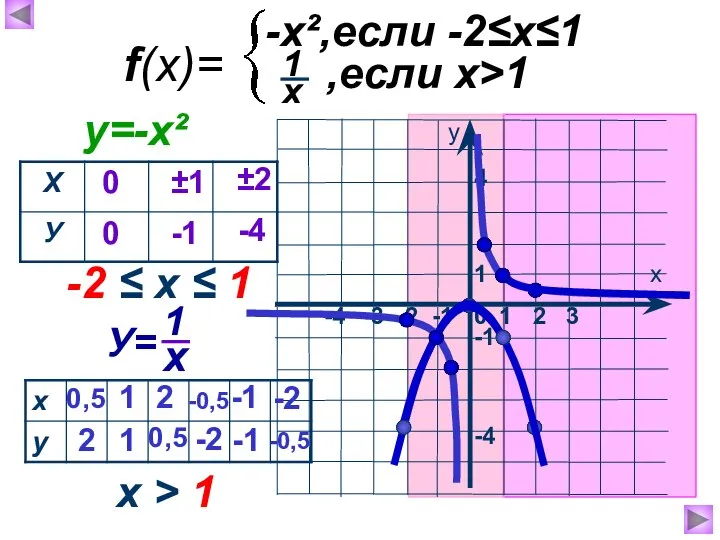
- 16. f(x)= -x²,если -2≤х≤1 ,если х>1 Постройте график функции и опишите её свойства.
- 17. 1 х у 0 -3 -2 -1 -4 -1 -4 1 2 3 4 f(x)= -x²,если
- 19. Скачать презентацию

 Итерактивная мозаика
Итерактивная мозаика Числовыe последовательности
Числовыe последовательности Окружность. 7 класс
Окружность. 7 класс Задачи на движение
Задачи на движение Двойные и тройные интегралы
Двойные и тройные интегралы Построение сечений многогранников
Построение сечений многогранников Интервальные оценки
Интервальные оценки Геометрические фигуры вокруг нас
Геометрические фигуры вокруг нас Снеговик - почтовик. Группа 4 -летки
Снеговик - почтовик. Группа 4 -летки Презентация на тему Построение сечений: метод следа
Презентация на тему Построение сечений: метод следа  Смежные и вертикальные углы
Смежные и вертикальные углы ЕГЭ. Экономические задачи IV
ЕГЭ. Экономические задачи IV Решение задач
Решение задач Преобразование формул
Преобразование формул Корень n-ой степени
Корень n-ой степени 7badff53-fae3-4f94-8d75-de14f449e5f4
7badff53-fae3-4f94-8d75-de14f449e5f4 О графиках
О графиках Sin, Cos, Tg острого угла прямоугольного треугольника
Sin, Cos, Tg острого угла прямоугольного треугольника Презентация на тему Математика - царица наук
Презентация на тему Математика - царица наук  Правила теории вероятности
Правила теории вероятности Обучение для выполнения НИР 5 курса. Занятие №3
Обучение для выполнения НИР 5 курса. Занятие №3 Деление отрезка на равные части с помощью циркуля и линейки
Деление отрезка на равные части с помощью циркуля и линейки Разложение вектора по базису
Разложение вектора по базису Устный счет
Устный счет Предыстория математического анализа. Значение производной в различных областях науки
Предыстория математического анализа. Значение производной в различных областях науки Презентация на тему Прямоугольный треугольник - готовая презентация, для решения на готовых чертежах.
Презентация на тему Прямоугольный треугольник - готовая презентация, для решения на готовых чертежах.  Устный счет. Действия с числами
Устный счет. Действия с числами Решение систем линейных уравнений способом подстановки
Решение систем линейных уравнений способом подстановки