Содержание
- 2. Решение простейших тригонометрических неравенств. Тригонометрическими неравенствами называются неравенства, содержащие переменную в аргументе тригонометрической функции.
- 3. Решение простейших тригонометрических неравенств. 0 sin x cos x a
- 4. Решение простейших тригонометрических неравенств. 0 sin x cos x a
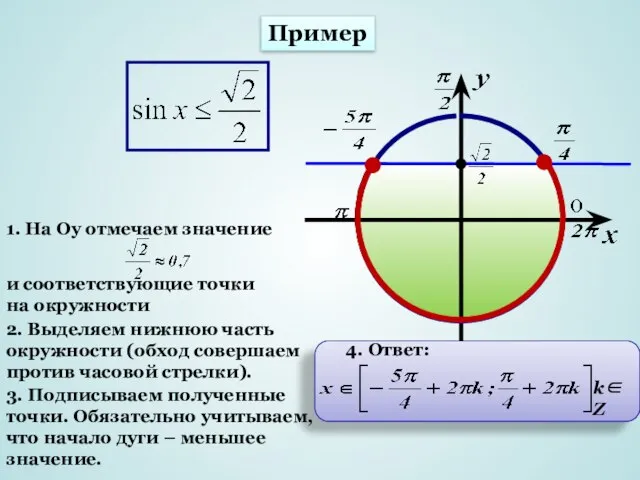
- 5. 1. На Оу отмечаем значение и соответствующие точки на окружности 2. Выделяем нижнюю часть окружности (обход
- 6. Решение простейших тригонометрических неравенств. 0 sin x cos x a
- 7. Решение простейших тригонометрических неравенств. 0 sin x cos x a
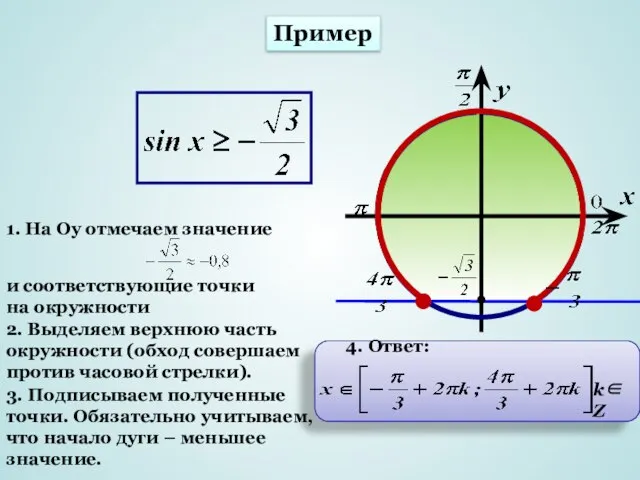
- 8. Пример 1. На Оу отмечаем значение и соответствующие точки на окружности 2. Выделяем верхнюю часть окружности
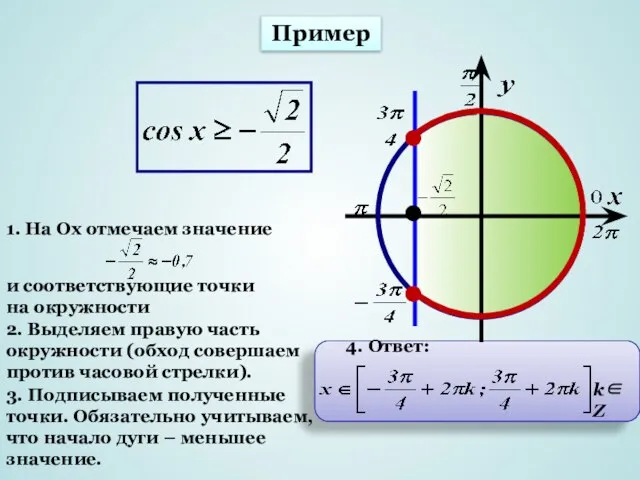
- 9. Пример 1. На Ох отмечаем значение и соответствующие точки на окружности 2. Выделяем правую часть окружности
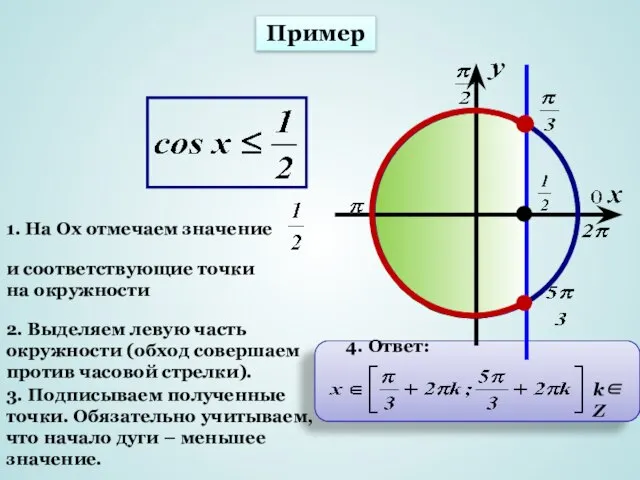
- 10. Пример k∈Z 1. На Ох отмечаем значение и соответствующие точки на окружности 2. Выделяем левую часть
- 11. Решение простейших тригонометрических неравенств. 0 sin x cos x a tg x
- 12. Решение простейших тригонометрических неравенств. 0 sin x cos x a tg x
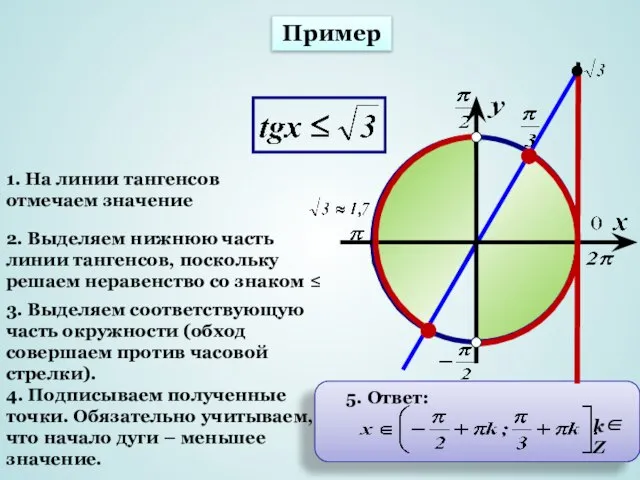
- 13. k∈Z 5. Ответ: 1. На линии тангенсов отмечаем значение 2. Выделяем нижнюю часть линии тангенсов, поскольку
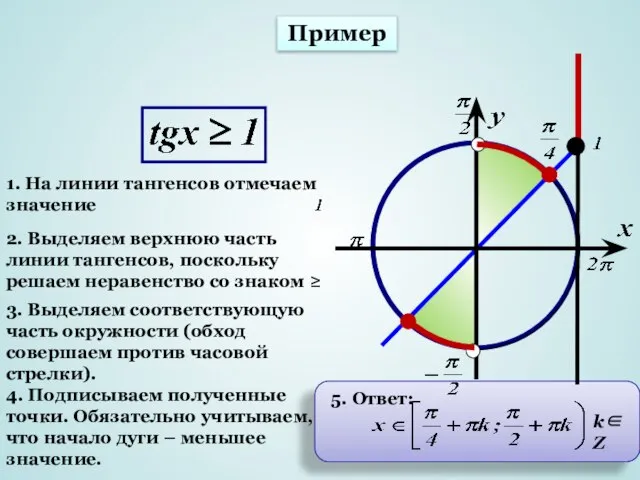
- 14. Пример k∈Z 5. Ответ: 1. На линии тангенсов отмечаем значение 2. Выделяем верхнюю часть линии тангенсов,
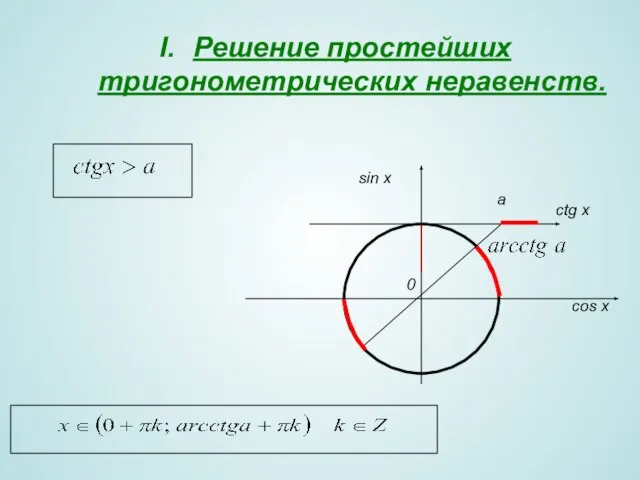
- 15. Решение простейших тригонометрических неравенств. 0 sin x cos x a сtg x
- 17. Скачать презентацию







 Упражнения для подготовки к ОГЭ по математике, задание №8
Упражнения для подготовки к ОГЭ по математике, задание №8 predmet_stereometrii._aksiomy_stereometrii
predmet_stereometrii._aksiomy_stereometrii Дифференциальные уравнения (продолжение)
Дифференциальные уравнения (продолжение) Алгоритм отыскания производной
Алгоритм отыскания производной Натуральные и целые числа
Натуральные и целые числа Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ  Пифагор и его школа
Пифагор и его школа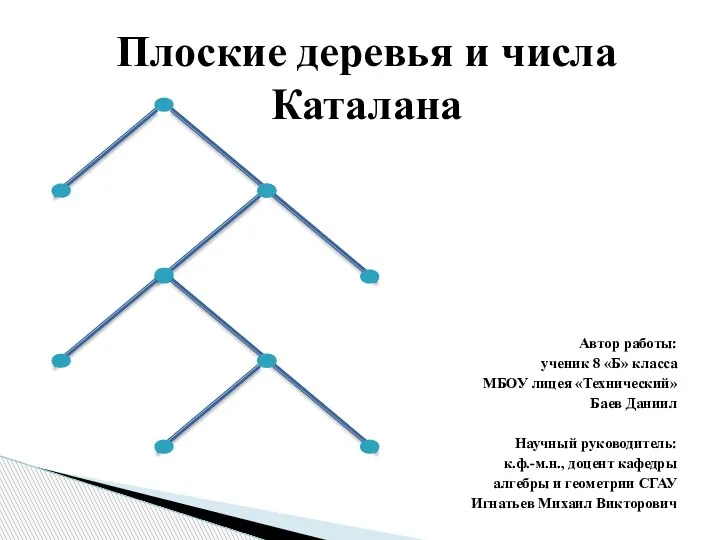 Плоские деревья и числа Каталана
Плоские деревья и числа Каталана Развитие учебных навыков через применение наглядных пособий и перевода математических задач в практическую плоскость
Развитие учебных навыков через применение наглядных пособий и перевода математических задач в практическую плоскость Действия с многозначными числами
Действия с многозначными числами Задачи, решаемые геометрическим моделированием
Задачи, решаемые геометрическим моделированием Степень с натуральным показателем. Занимательные задания
Степень с натуральным показателем. Занимательные задания Построение графика функции
Построение графика функции Матрицы и определители
Матрицы и определители Сложение и вычитание десятичных дробей. Урок – смотр знаний. 5 класс
Сложение и вычитание десятичных дробей. Урок – смотр знаний. 5 класс Методы решения СЛДУ
Методы решения СЛДУ Обратная матрица
Обратная матрица Вычитание векторов
Вычитание векторов Линейные пространства и линейные операторы. Лекция 6
Линейные пространства и линейные операторы. Лекция 6 Задачи с параметрами
Задачи с параметрами Презентация на тему Вычитание с переходом через десяток
Презентация на тему Вычитание с переходом через десяток  Вычисление производной степенной
Вычисление производной степенной Задача о трех игральных костях. Элементарный способ
Задача о трех игральных костях. Элементарный способ Понятие десятичной дроби. Чтение и запись десятичных дробей
Понятие десятичной дроби. Чтение и запись десятичных дробей Математическое моделирование. Тестирование
Математическое моделирование. Тестирование Степень числа
Степень числа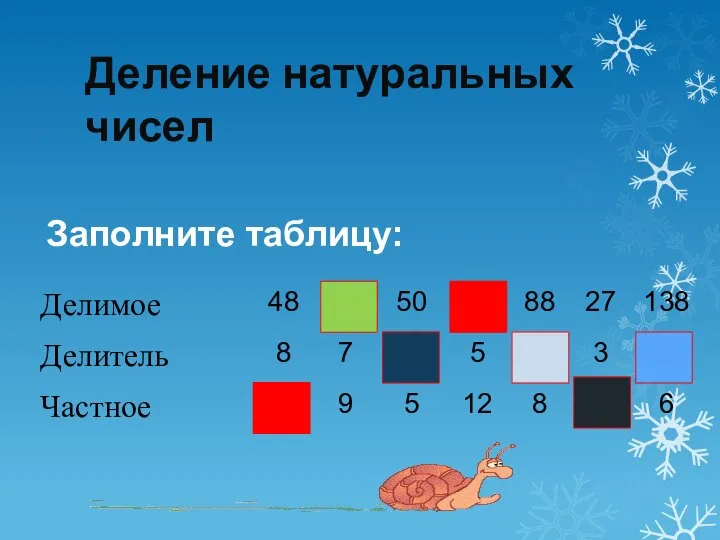 Деление натуральных чисел
Деление натуральных чисел Числа 1 – 10. Сложение и вычитание
Числа 1 – 10. Сложение и вычитание