Содержание
- 2. Цель: ознакомить учащихся с принципом определения трегольника по стороне и прилежащие к ней углы
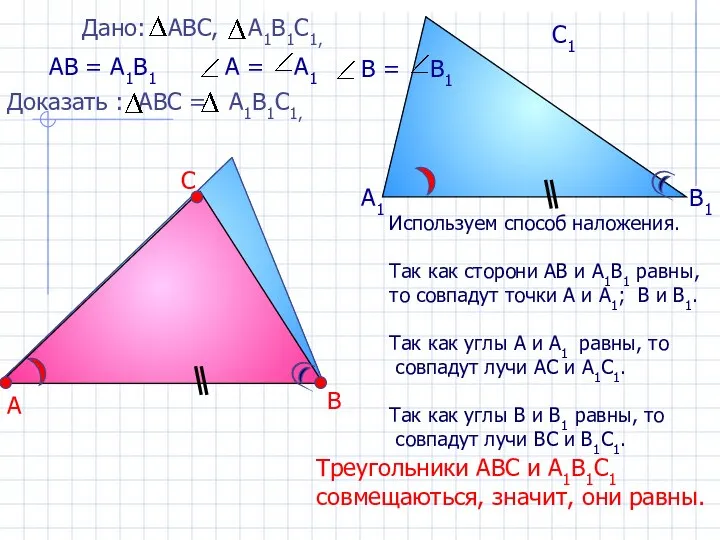
- 3. Просмотрите внимательно правильную запись этой задачи Дано: АО=ОС, ВО=ОД Доказать:ΔАОВ и ΔСОД Повторим!!!!! Доказательство: Рассмотрим ΔАОВ
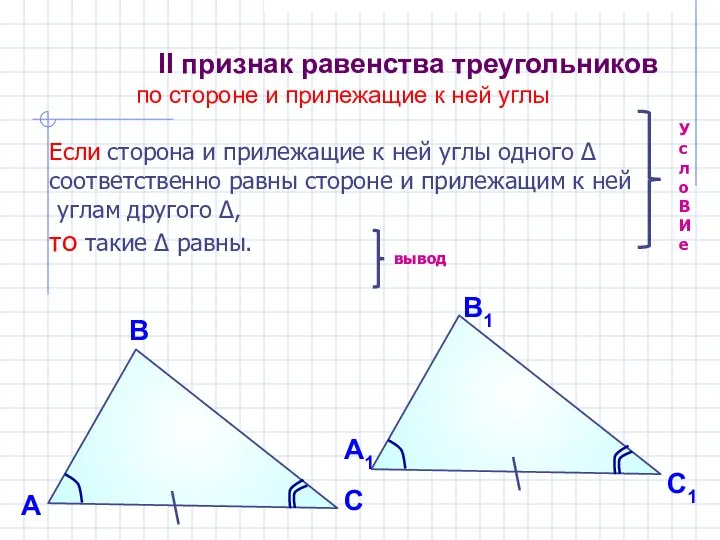
- 4. II признак равенства треугольников по стороне и прилежащие к ней углы Если сторона и прилежащие к
- 5. А В С А1 В1 С1 АВ = А1В1 Треугольники АВС и А1В1С1 совмещаються, значит, они
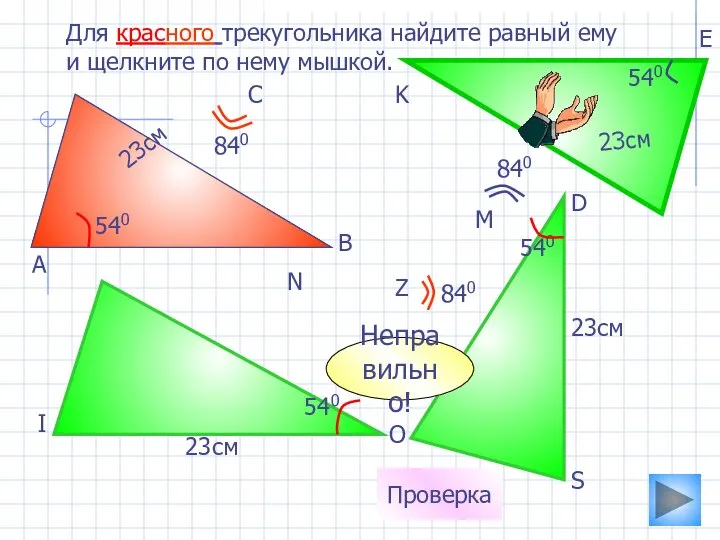
- 6. 23см 540 Для красного трекугольника найдите равный ему и щелкните по нему мышкой. 23см 23см 540
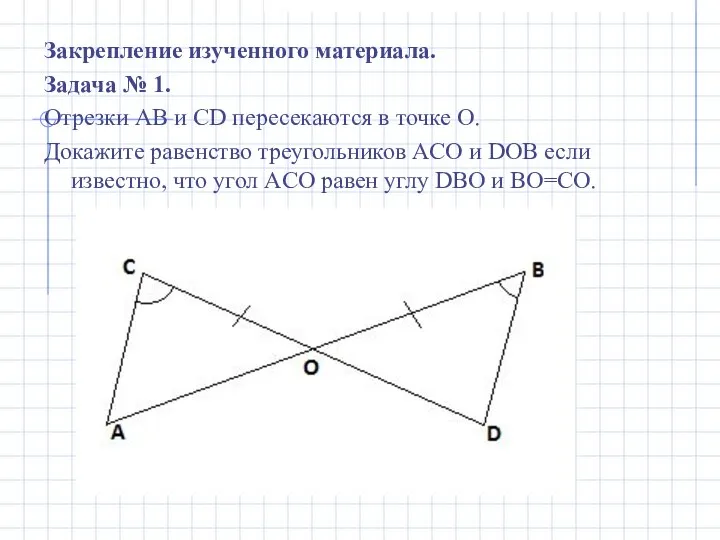
- 7. Закрепление изученного материала. Задача № 1. Отрезки AB и CD пересекаются в точке O. Докажите равенство
- 8. Решение: Рассмотрим ∆ ACO и ∆ DBO: BO=CO (по условию) Следственно ∆ ACO = ∆ DBO
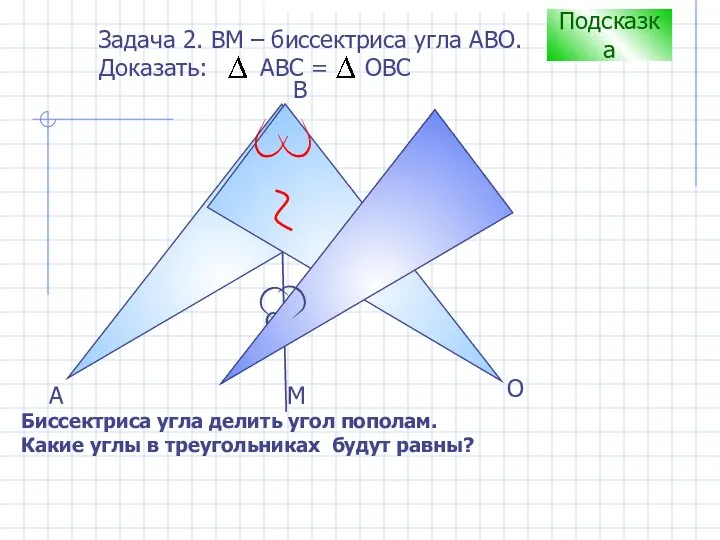
- 9. С B А Задача 2. ВM – биссектриса угла АВО. Доказать: АВС = ОВС Подсказка Биссектриса
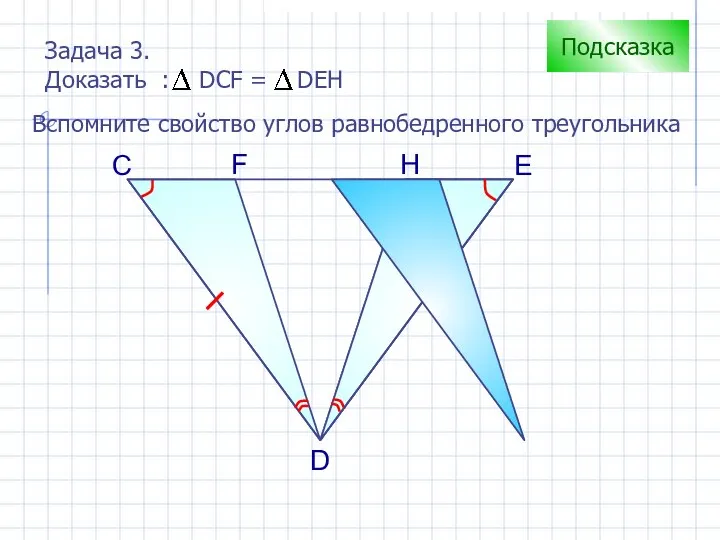
- 10. С H D F E Подсказка Вспомните свойство углов равнобедренного треугольника
- 11. Это интересно!!!!!!!!
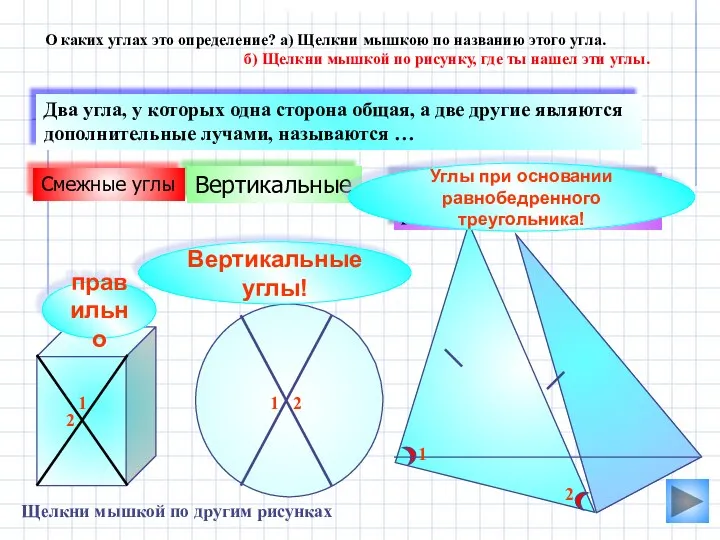
- 12. Вертикальные углы! Вертикальные Кути при основі рівнобедреного трикутника Два угла, у которых одна сторона общая, а
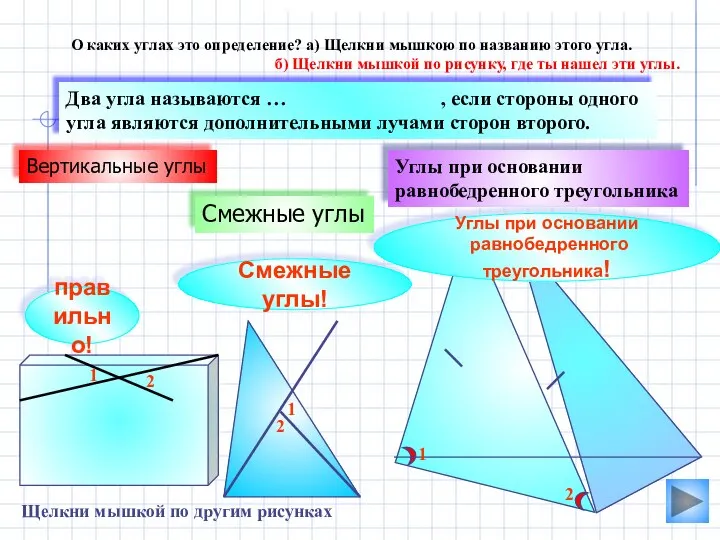
- 13. Смежные углы Углы при основании равнобедренного треугольника Два угла называются … , если стороны одного угла
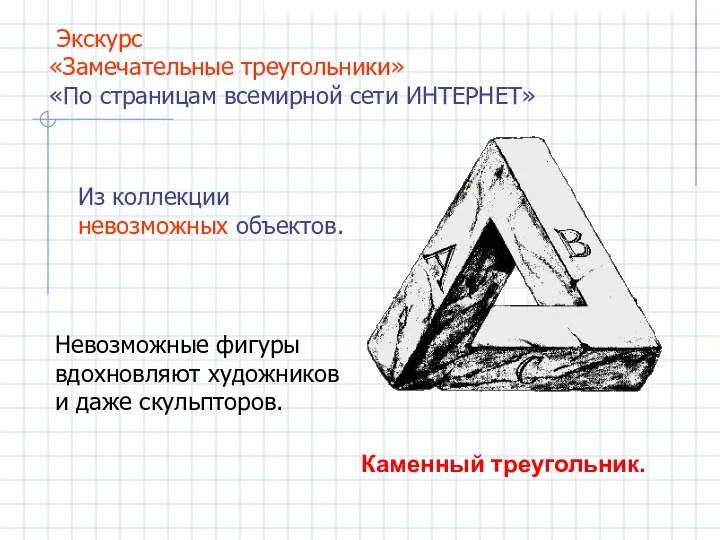
- 14. Каменный треугольник. Невозможные фигуры вдохновляют художников и даже скульпторов. Экскурс «Замечательные треугольники» «По страницам всемирной сети
- 15. Треугольник Пенроуза или трибар. Из коллекции невозможных объектов. Кажется, что мы видим три бруска квадратного сечения
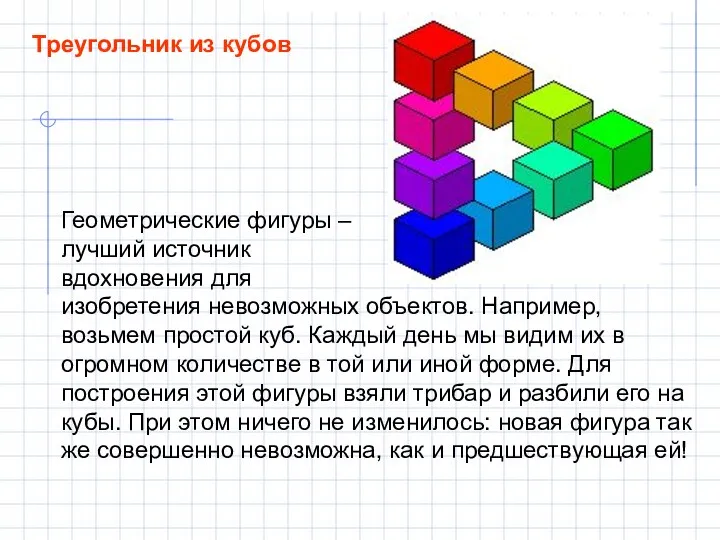
- 16. Треугольник из кубов Геометрические фигуры – лучший источник вдохновения для изобретения невозможных объектов. Например, возьмем простой
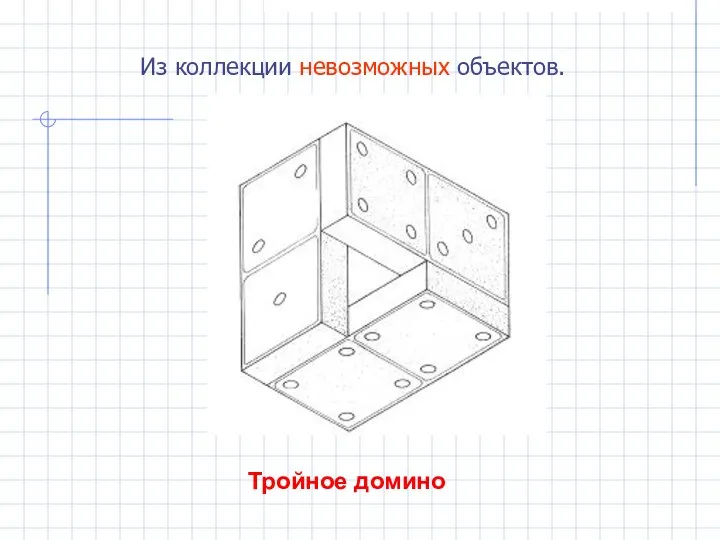
- 17. Тройное домино Из коллекции невозможных объектов.
- 18. На примере первого трибара можно было увидеть лишь одно невозможное соединение, а в этой фигуре –
- 19. Треугольник с перемычками Из коллекции невозможных объектов.
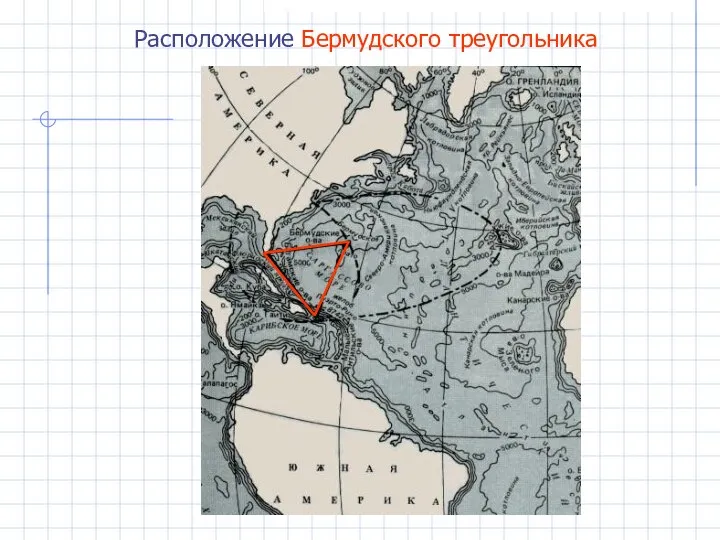
- 20. Расположение Бермудского треугольника
- 21. Бермудский треугольник — район в Атлантическом океане, в котором происходят якобы таинственные исчезновения морских и воздушных
- 22. Скептики утверждают, однако, что исчезновения судов в бермудском треугольнике происходят не чаще, чем в других районах
- 24. Скачать презентацию









 Теорема Пифагора
Теорема Пифагора Вывод формулы Герона. Геометрия 8 класс
Вывод формулы Герона. Геометрия 8 класс Coordinate plane
Coordinate plane Шар и сфера
Шар и сфера Применение производной
Применение производной Помогают законы. 5 - 7 класс
Помогают законы. 5 - 7 класс Многоугольник
Многоугольник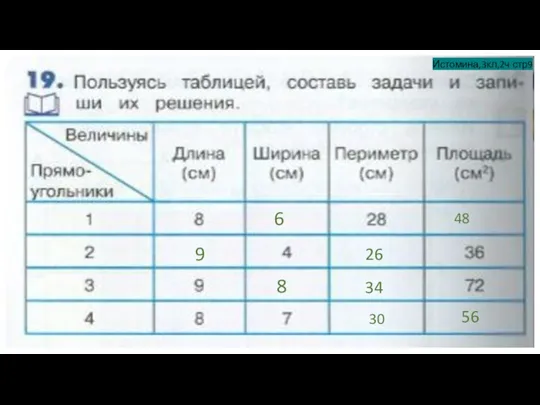 Величины. Составление задач
Величины. Составление задач Математика для дошкольников (средняя группа)
Математика для дошкольников (средняя группа) Кто живет под грибом
Кто живет под грибом Задачи для практики
Задачи для практики Введение в геометрию
Введение в геометрию Логическая задача. Способы решения
Логическая задача. Способы решения Презентация по математике "Величины. Объём" -
Презентация по математике "Величины. Объём" -  Презентация на тему Волейбол. Передача сверху
Презентация на тему Волейбол. Передача сверху  Алгебраическая дробь и её основное свойство. 7 класс
Алгебраическая дробь и её основное свойство. 7 класс Задачи на расстояния в пространстве
Задачи на расстояния в пространстве Как умножали египтяне
Как умножали египтяне Степень с натуральным показателем и его свойства
Степень с натуральным показателем и его свойства Презентация по математике "Число 7" -
Презентация по математике "Число 7" -  Симметрия в геометрии и в жизни
Симметрия в геометрии и в жизни Классификация функций
Классификация функций Математика
Математика Показательное уравнение
Показательное уравнение Алгебра. Дроби. Сумма дробей
Алгебра. Дроби. Сумма дробей Координатная плоскость
Координатная плоскость Чётность и не чётность тригонометрических функций
Чётность и не чётность тригонометрических функций Числовая последовательность
Числовая последовательность