Методика ознакомления обучающихся с геометрическими фигурами (прямой, ломаной) и их свойствами

Методика ознакомления учащихся с геометрическими фигурами связана с задачами изучения темы:
1. Формировать четкие представления о таких геометрических фигурах, как точка, отрезок, угол, многоугольник, прямоугольник, квадрат и.т.д.
2. Формировать практические умения и навыки построения геометрических фигур, как с помощью чертёжных инструментов так и без них.
3. Развивать пространственные представления учащихся.

В курсе математики геометрический материал должен представлять четкую систему, которая позволит ученику последовательно (в логике развития ПМ младших школьников как основной развивающей цели) овладеть образами геометрических фигур и геометрических отношений, которые в курсе основной и старшей школы будут изучаться на уровне понятий. Иными словами, в начальной школе фактически формируется база геометрических понятий.

В программе четко определены и требования к знаниям и умениям детей о геометрических фигурах. Учитель должен добиться усвоения детьми названий изучаемых геометрических фигур и их свойств, а также сформировать умение выполнять их построение на клетчатой бумаге. Отмечая особенности изучения геометрических фигур в начальных классах, следует обратить внимание на то обстоятельство, что свойства всех изучаемых фигур выявляются экспериментальным путем в ходе выполнения соответствующих упражнений. Систематически должны проводиться такие виды работ, как изготовление геометрических фигур из бумаги, палочек, пластилина, их вырезание, моделирование и др. При этом важно учить детей различать существенные и несущественные признаки фигур. Большое внимание при этом следует уделить использованию приема сопоставления и противопоставления геометрических фигур.

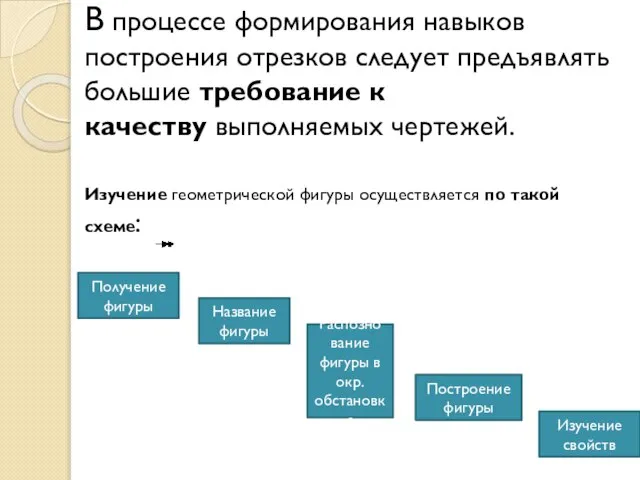
В процессе формирования навыков построения отрезков следует предъявлять большие требование к качеству выполняемых чертежей.
Изучение геометрической фигуры осуществляется по такой схеме:
Получение фигуры
Название фигуры
Распозно
вание фигуры в окр.обстановке
Построение фигуры
Изучение свойств

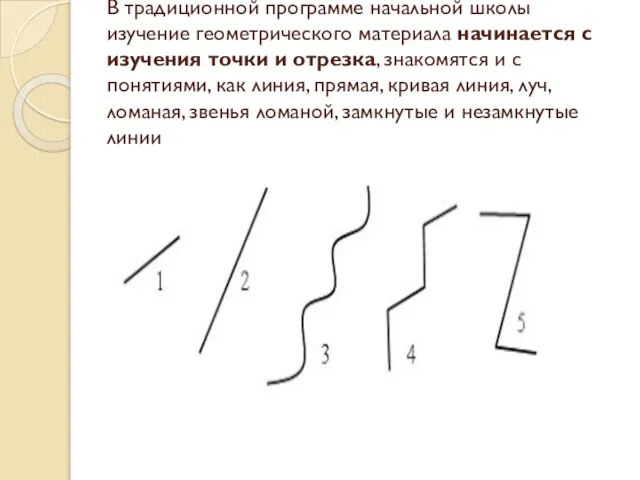
В традиционной программе начальной школы изучение геометрического материала начинается с изучения точки и отрезка, знакомятся и с понятиями, как линия, прямая, кривая линия, луч, ломаная, звенья ломаной, замкнутые и незамкнутые линии

СВОЙСТВА ПРЯМОЙ.
A) ПОЛОЖЕНИЕ ПРЯМОЙ ЛИНИИ ВПОЛНЕ ОПРЕДЕЛЯЕТСЯ ТЕМИ ДВУМЯ ТОЧКАМИ, МЕЖДУ КОТОРЫМИ ОНА ПРОВЕДЕНА.
ЭТО СВОЙСТВО ЗАВИСИТ ОТ ТОГО, ЧТО
B) МЕЖДУ ДВУМЯ ТОЧКАМИ МОЖНО ПРОВЕСТИ ТОЛЬКО ОДНУ ПРЯМУЮ ЛИНИЮ, ИБО МЕЖДУ ДВУМЯ ТОЧКАМИ СУЩЕСТВУЕТ ТОЛЬКО ОДНО КРАТЧАЙШЕЕ РАССТОЯНИЕ.
Прямая линия есть кратчайшее расстояние между двумя точками.

Определение прямой линии, вытекающее из непосредственного усмотрения ее свойства, некоторые называют аксиомой. Это понятие о прямой линии называют иногда основным.
В прямой линии нужно отличить ее положение и ее длину.
Прямую линию можно неопределенно продолжать в обе стороны.
Две точки определяют прямую линии не только в тех точках, которые лежат между ними, но и в тех точках, которые получаются, если неопределенно продолжать прямую линию в обе стороны.

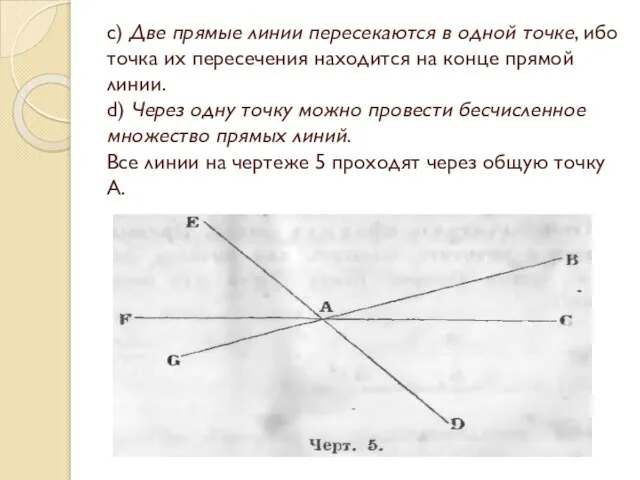
c) Две прямые линии пересекаются в одной точке, ибо точка их пересечения находится на конце прямой линии.
d) Через одну точку можно провести бесчисленное множество прямых линий.
Все линии на чертеже 5 проходят через общую точку A.

Две прямые линии, имеющие одинаковую длину, называются равными.

Сравнение прямых линий
Чтобы сравнить две данные прямые AB и CD по длине (черт. 7) накладывают линию CD на линию AB так, чтобы точка C совпадала с точкой A

Сложение и вычитание прямых линий. Прямые линии можно складывать и вычитать. Сложить или вычесть линии значит найти линию, длина которой равна сумме или разности длин данных линий.

Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

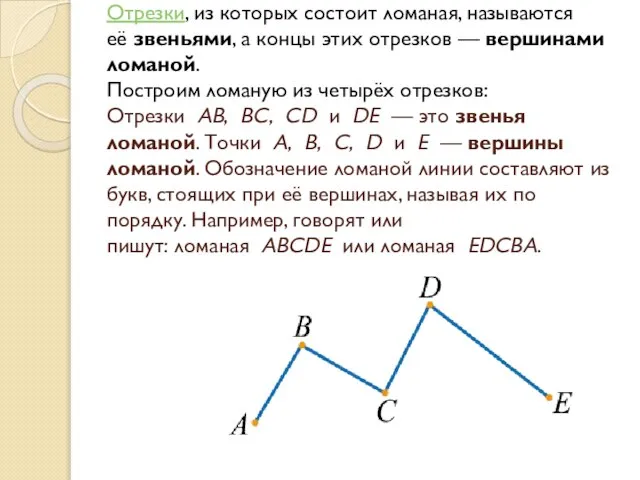
Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.
Построим ломаную из четырёх отрезков:
Отрезки AB, BC, CD и DE — это звенья ломаной. Точки A, B, C, D и E — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная ABCDE или ломаная EDCBA.

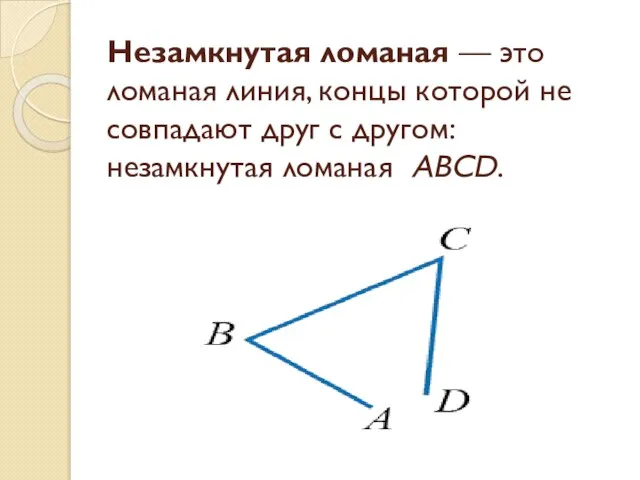
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:
незамкнутая ломаная ABCD.

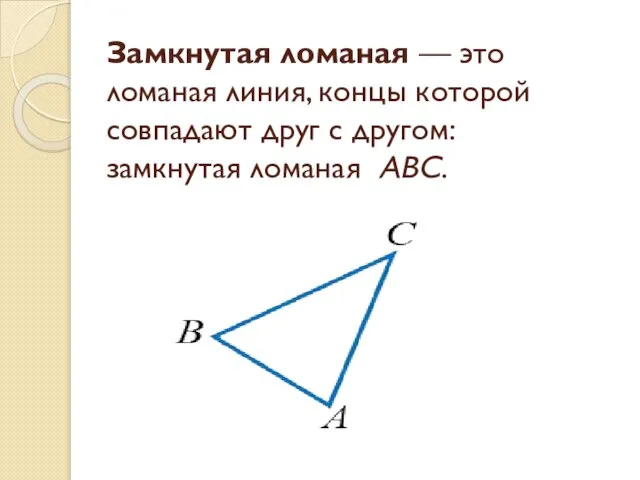
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:
замкнутая ломаная ABC.

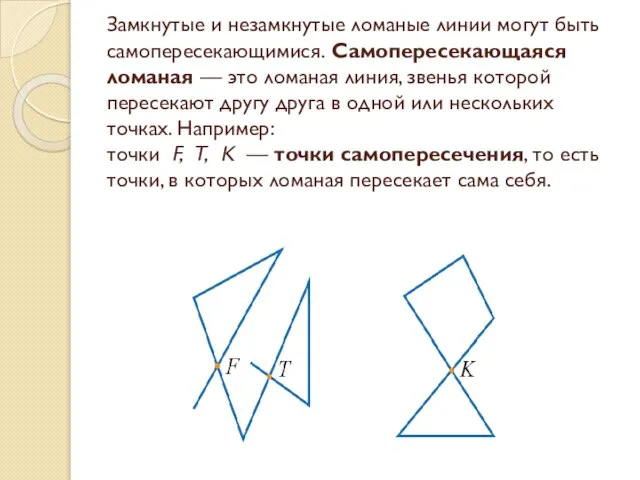
Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:
точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.

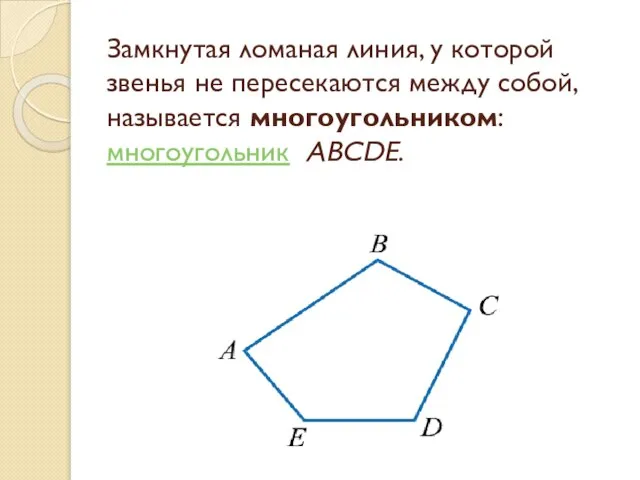
Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:
многоугольник ABCDE.

Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.

Важнейшую роль при изучении геометрического материала в начальных классах играют геометрические задания, специально направленные на развитие у младших школьников пространственных представлений и воображения, их речи и мышления, на формирование практических умений и навыков.
К ним можно отнести задания на:
-классификацию геометрических фигур;
-деление фигур на части;
-составление геометрических фигур заданной формы из других;
-вычленение фигур на чертеже сложной конфигурации;
-распознавание фигур знакомых видов в окружающей обстановке;
-выяснение геометрической формы предметов или их частей.

Для использования геометрического материала как средства обучения нужно, чтобы учащиеся имели уже соответствующие геометрические знания и умения. В то же время показателем геометрических знаний является умение учащихся применять приобретённые знания геометрии при решении каких-либо практических, не обязательно геометрических задач.