Параллельность прямой и плоскости. Лекция 5

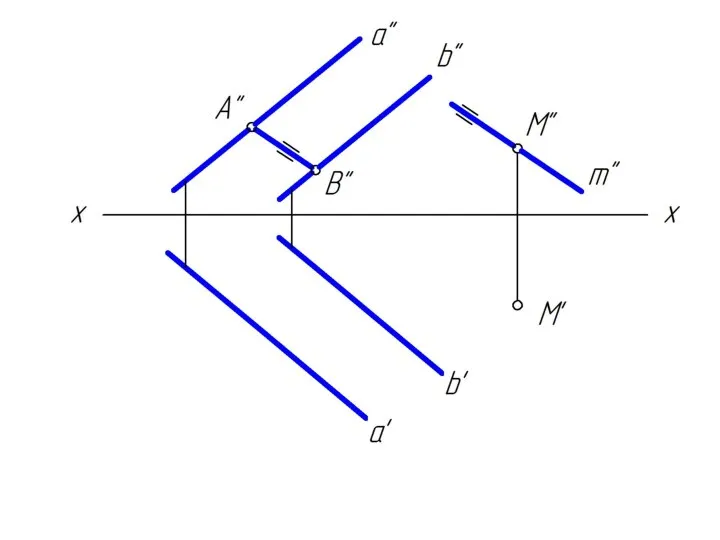
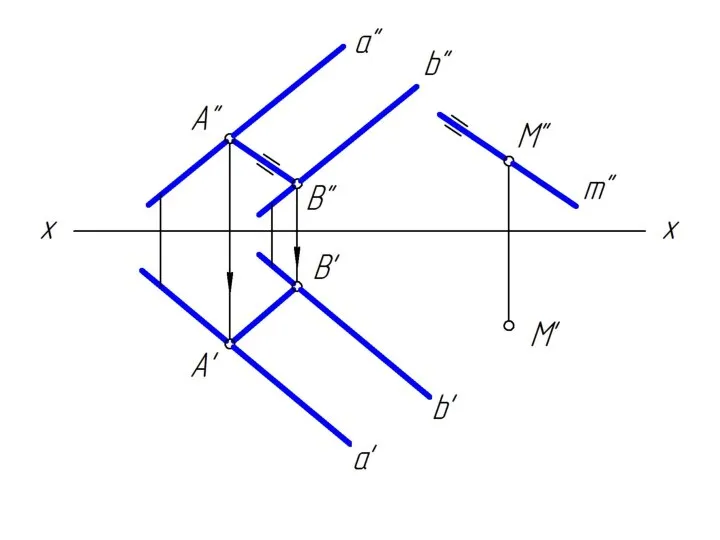
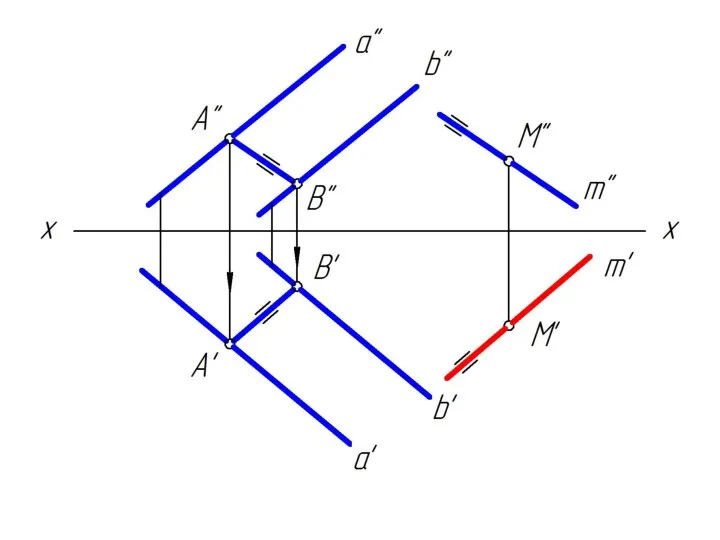
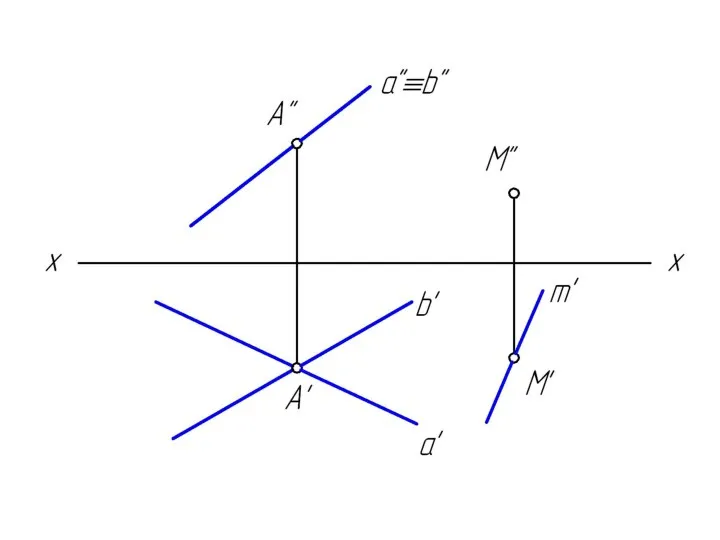
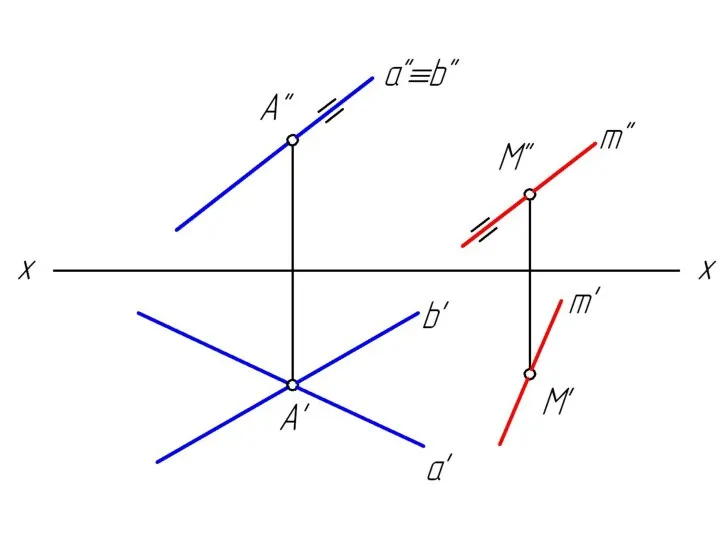
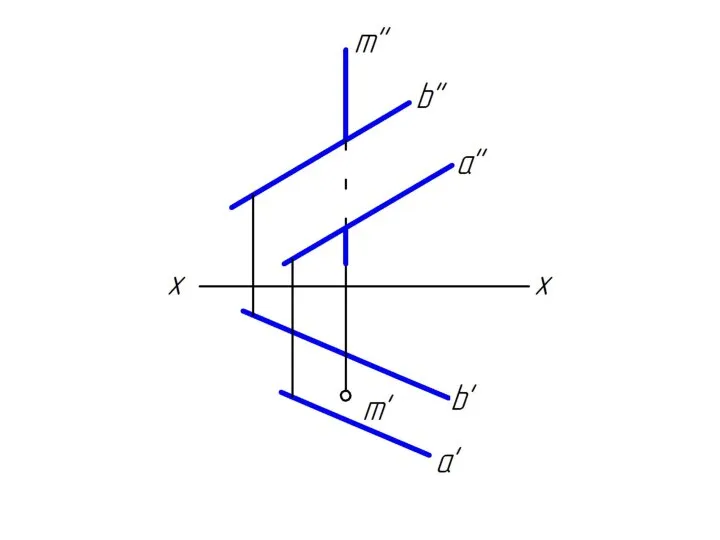
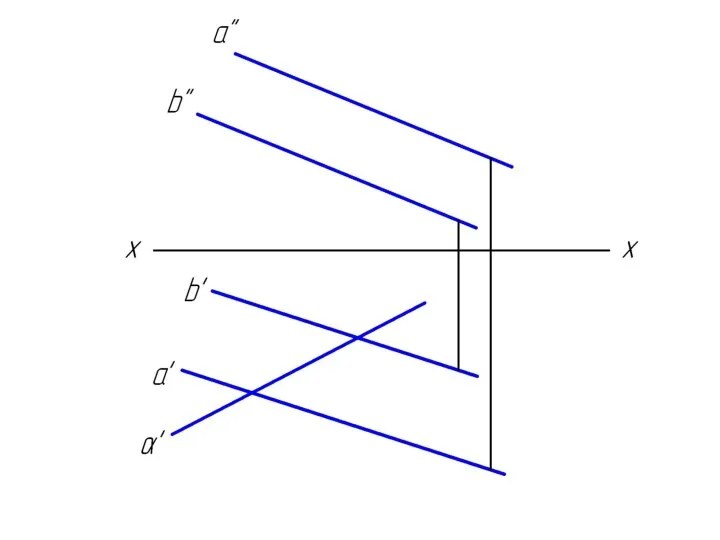
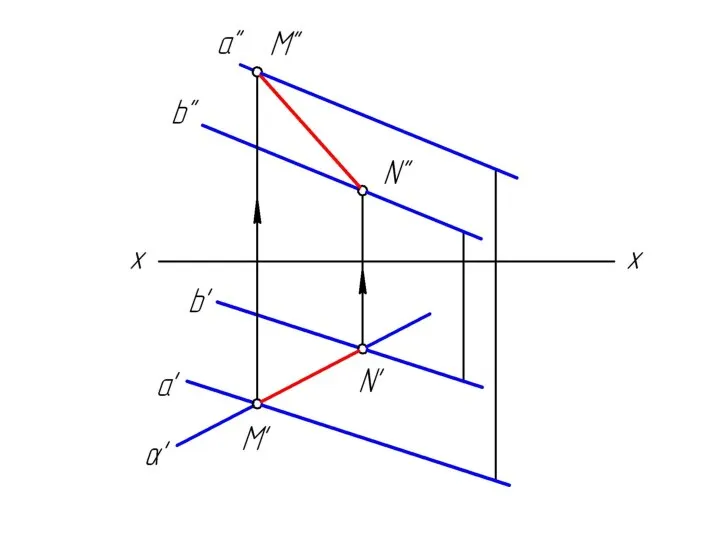
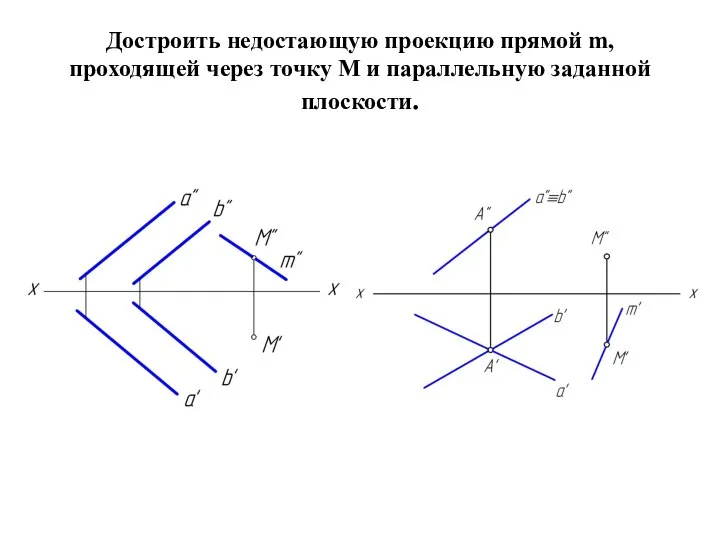
Достроить недостающую проекцию прямой m, проходящей через точку М и параллельную заданной плоскости.

Пересечение прямой с плоскостью
Задача по нахождению точки пересечения прямой с плоскостью входит в алгоритм решения широкого круга как позиционных, так и метрических задач.
Решение задачи значительно упрощается если прямая или плоскость занимает проецирующее положение.

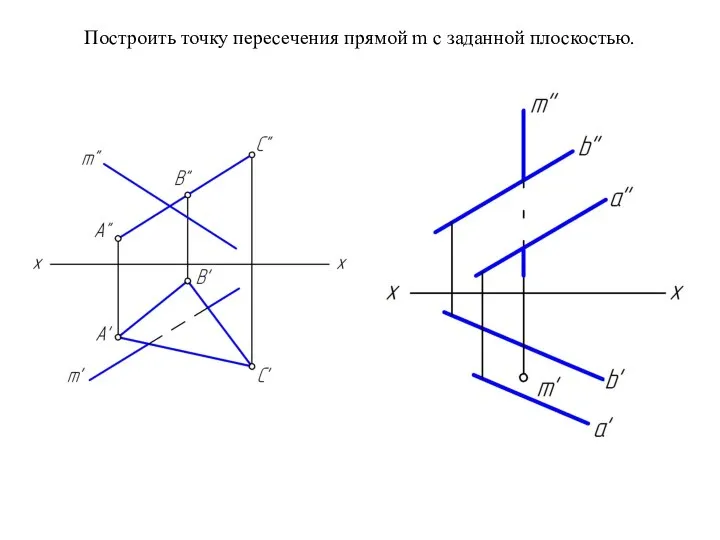
Построить точку пересечения прямой m с заданной плоскостью.

Для решения задачи на построение точки пересечения прямой общего положения с плоскостью общего положения необходимо уметь строить линию пересечения плоскости общего положения и проецирующей плоскости.
Линия пересечения таких плоскостей может быть построена без дополнительных построений, т.к. согласно свойству проецирующих плоскостей – все проекции точек, следовательно и линия пересечения этой плоскости с другой плоскостью, принадлежат проецирующему следу плоскости.

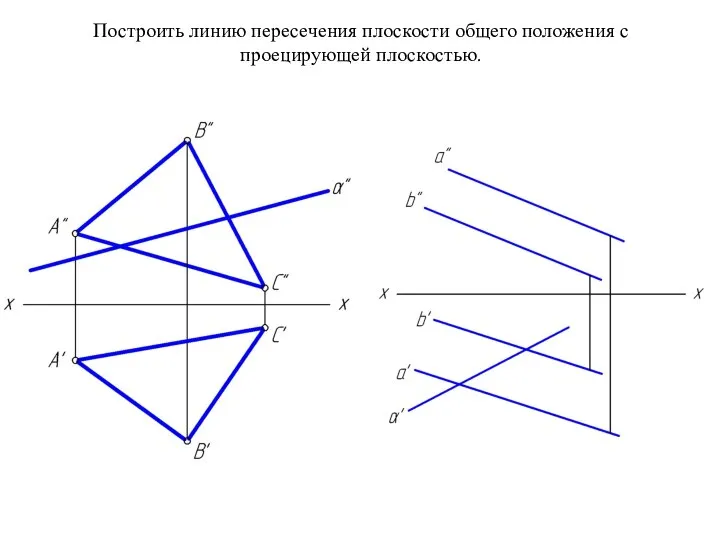
Построить линию пересечения плоскости общего положения с проецирующей плоскостью.

Пересечение прямой с плоскостью общего положения
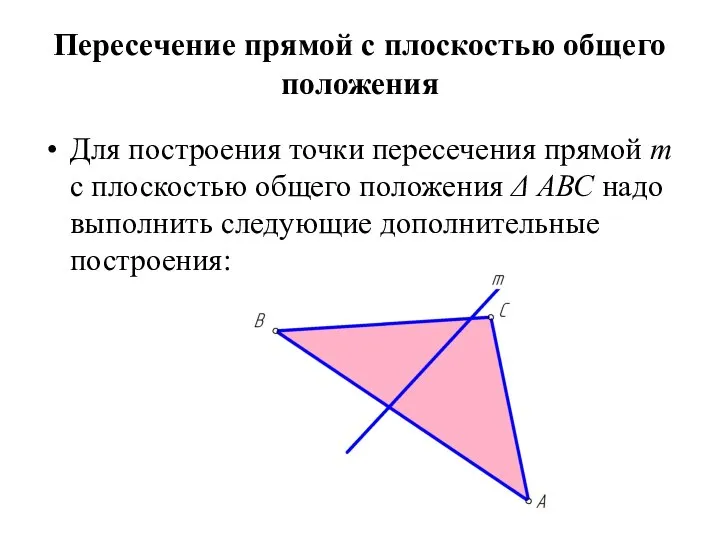
Для построения точки пересечения прямой m с плоскостью общего положения Δ АВС надо выполнить следующие дополнительные построения:

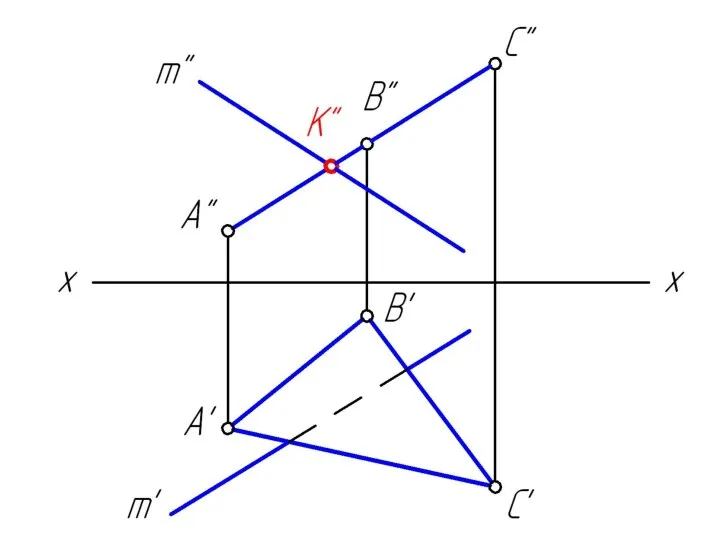
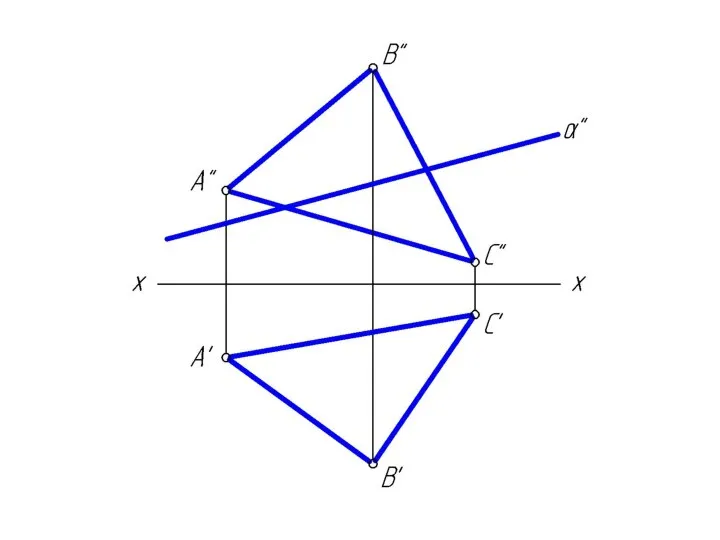
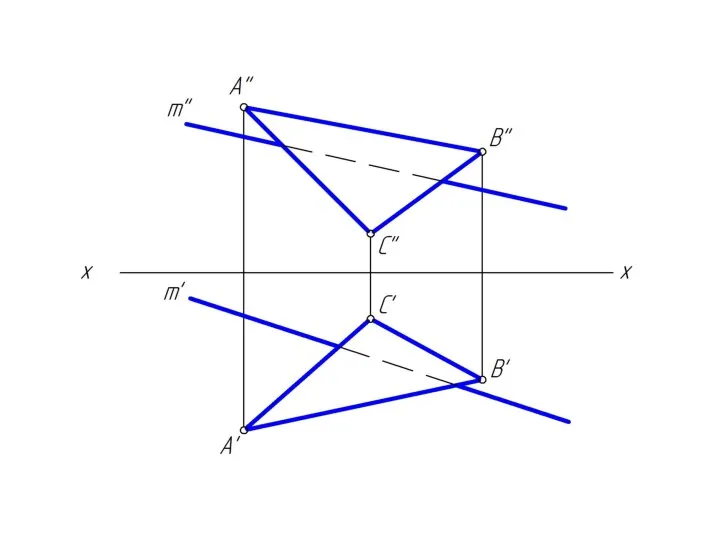
1. через заданную прямую m провести вспомогательную проецирующую плоскость β;

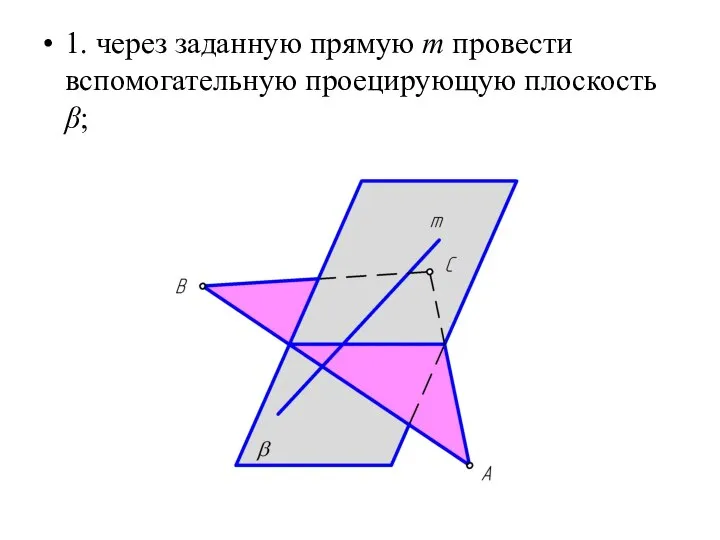
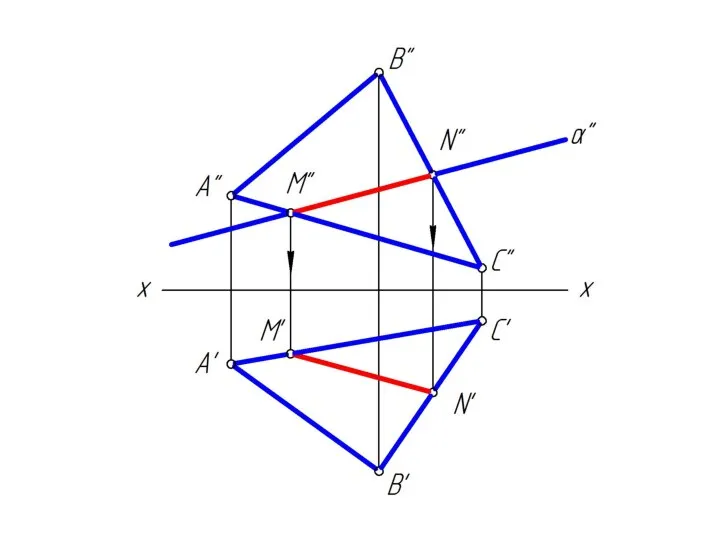
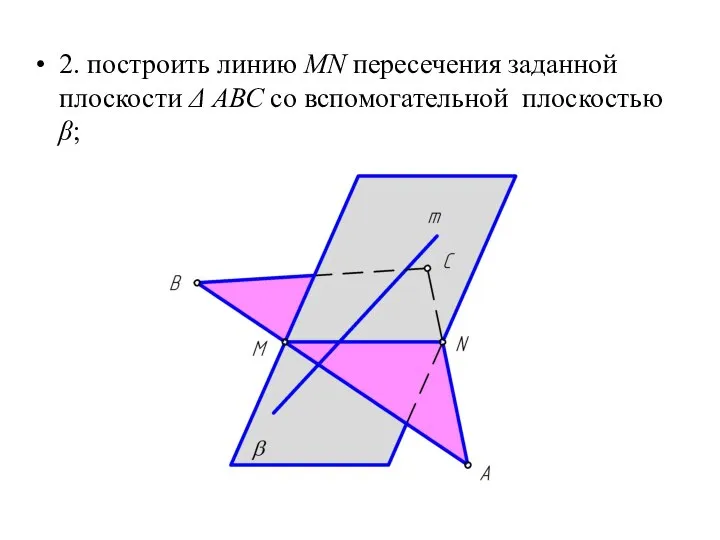
2. построить линию MN пересечения заданной плоскости Δ АВС со вспомогательной плоскостью β;

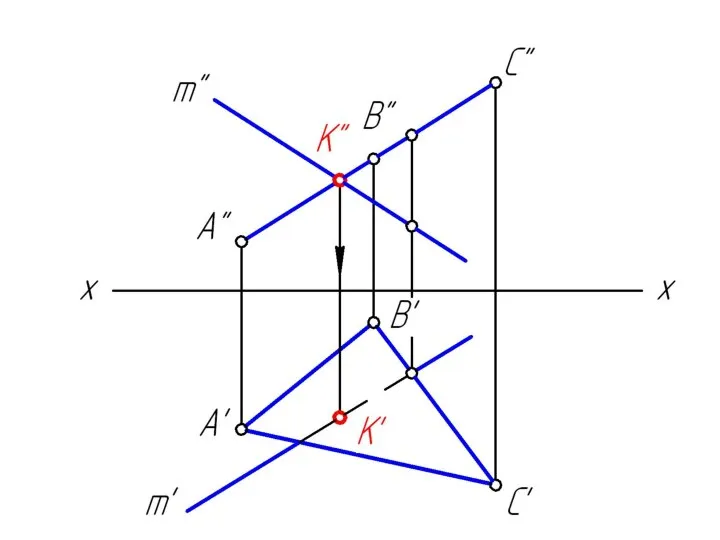
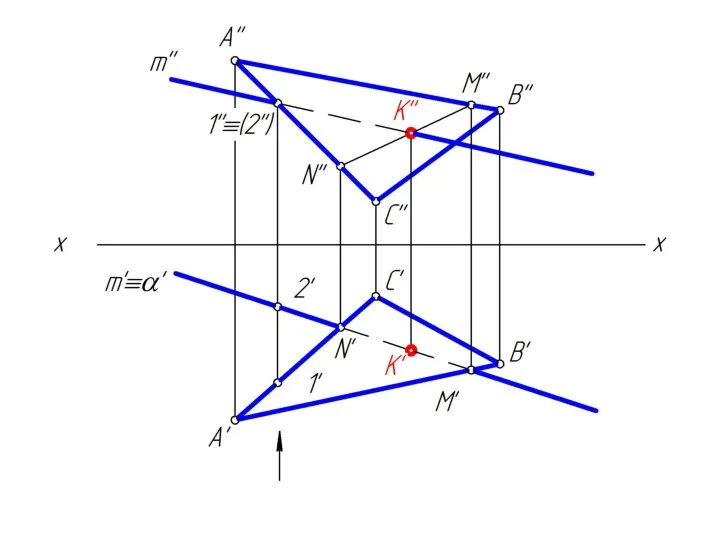
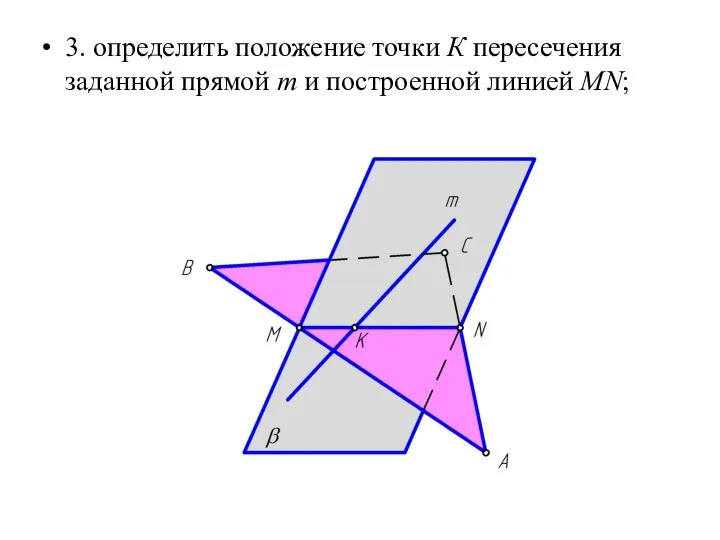
3. определить положение точки К пересечения заданной прямой m и построенной линией MN;

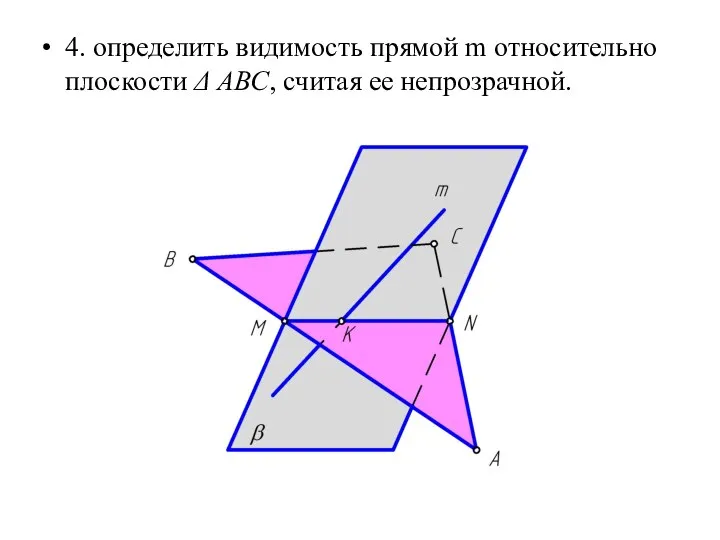
4. определить видимость прямой m относительно плоскости Δ АВС, считая ее непрозрачной.

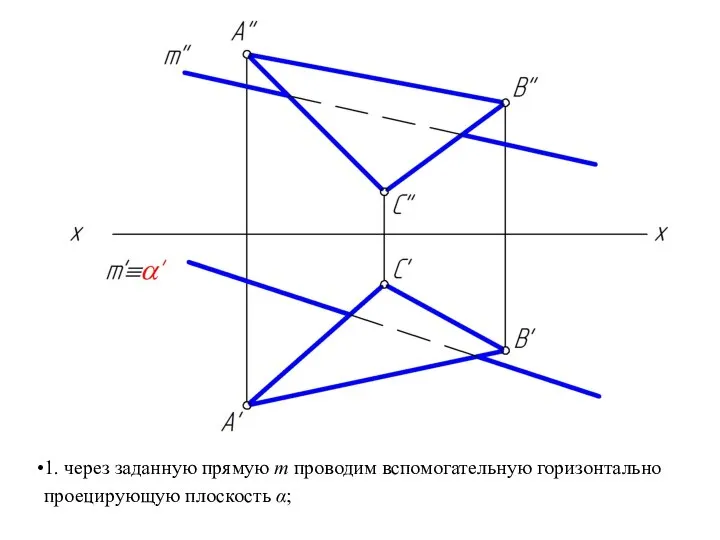
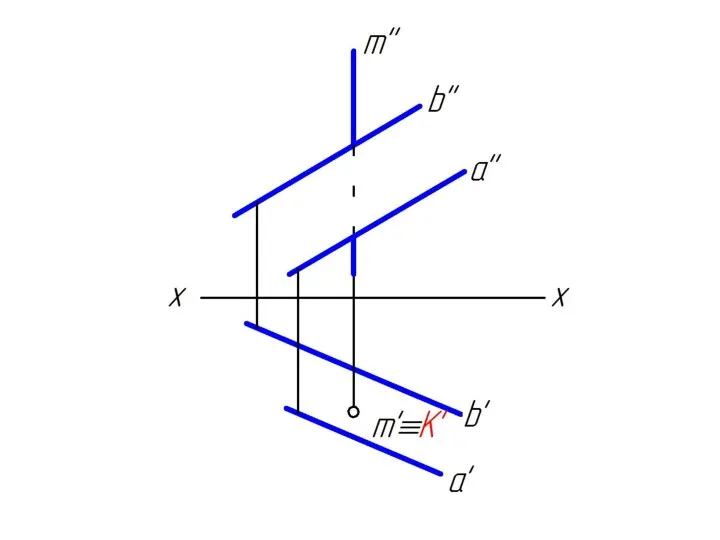
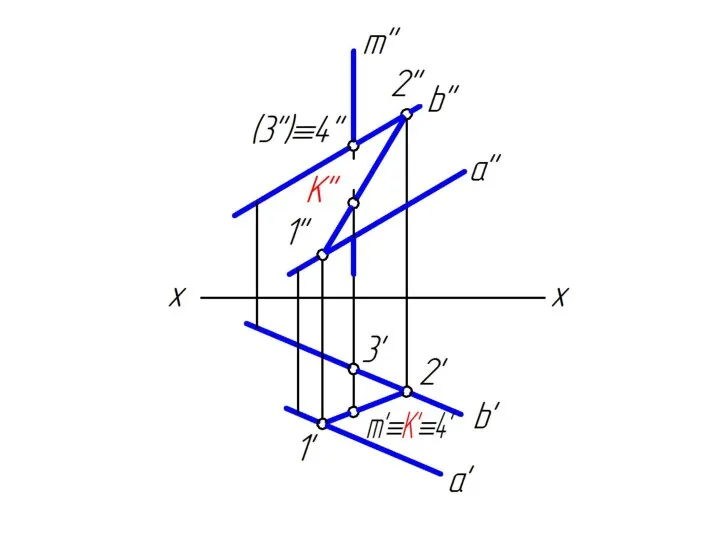
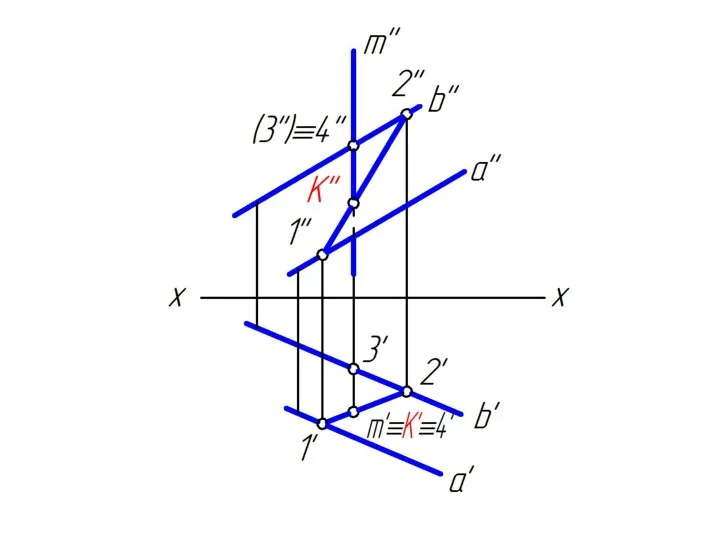
1. через заданную прямую m проводим вспомогательную горизонтально
проецирующую плоскость α;

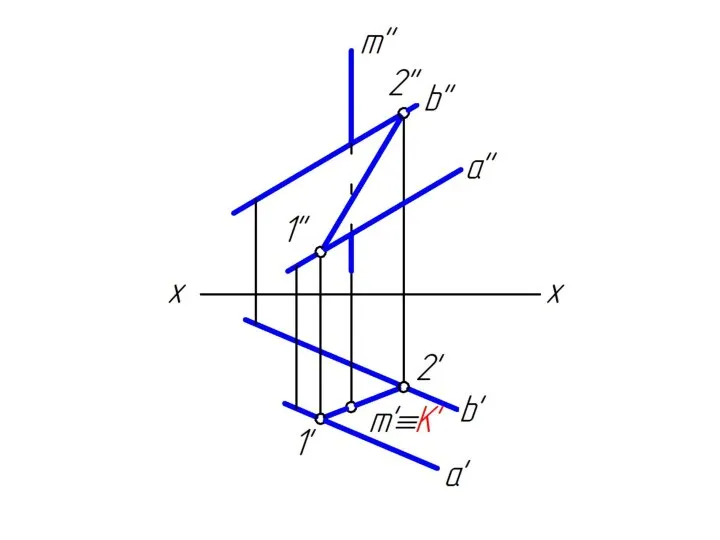
2. строим линию пересечения MN заданной плоскости Δ АВС
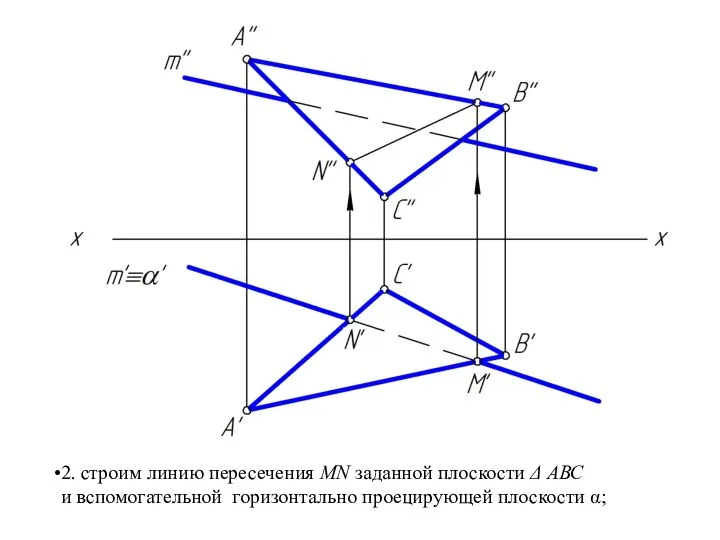
и вспомогательной горизонтально проецирующей плоскости α;

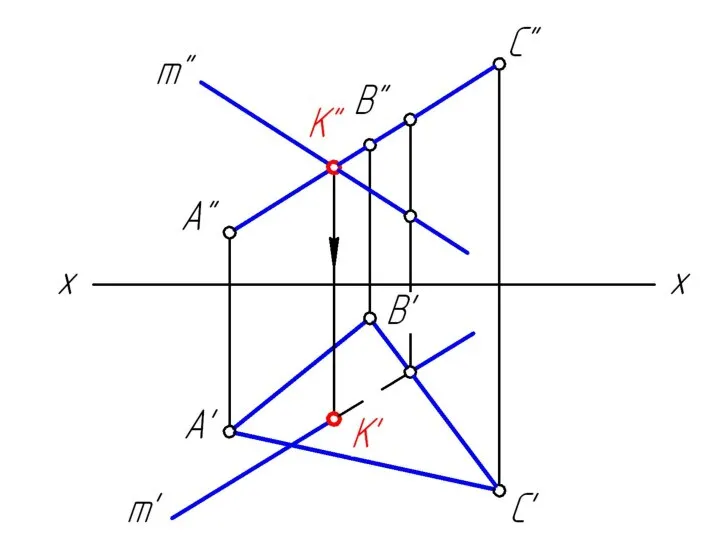
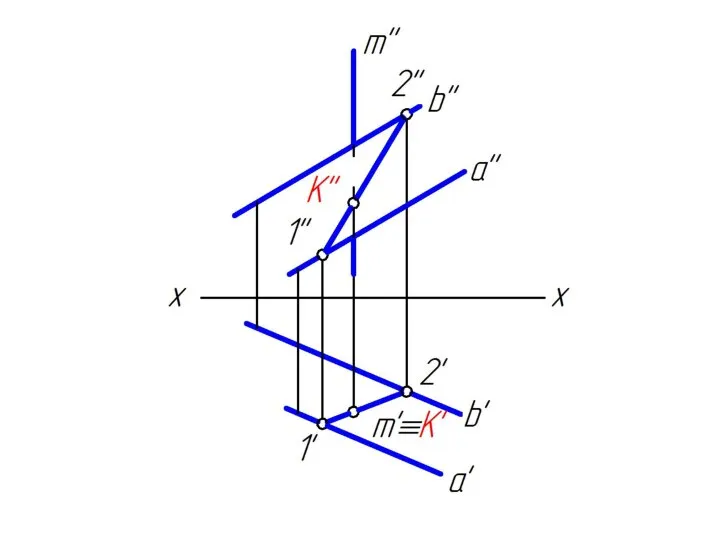
3. определяем положение точки К пересечения заданной прямой m и
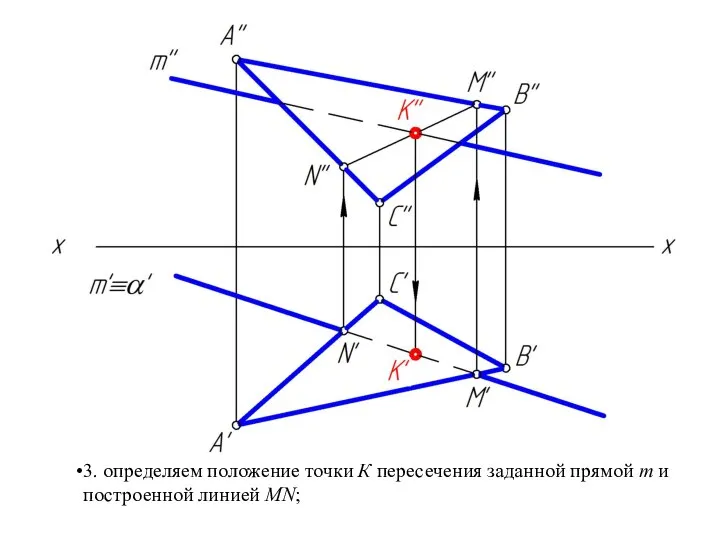
построенной линией MN;

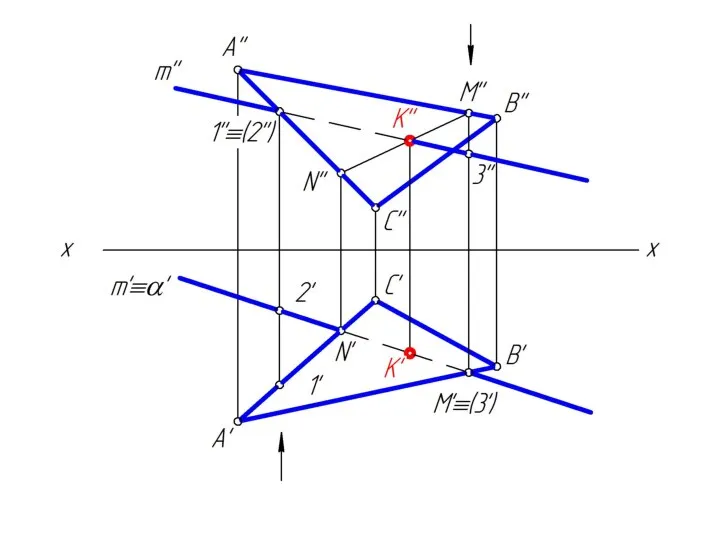
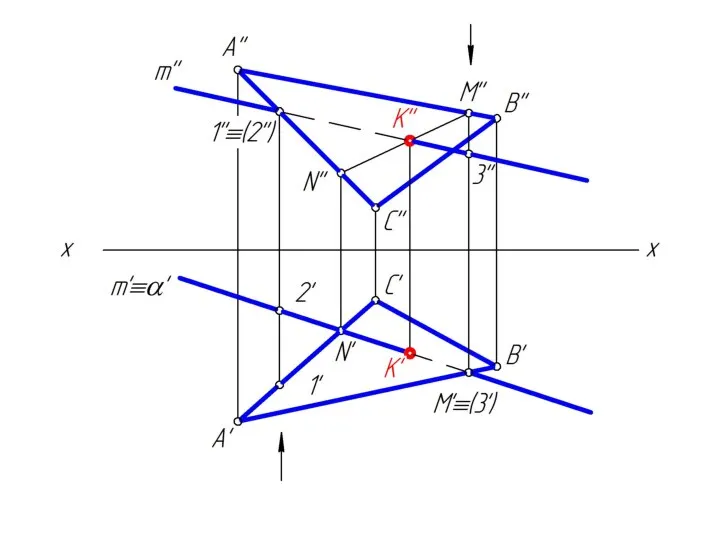
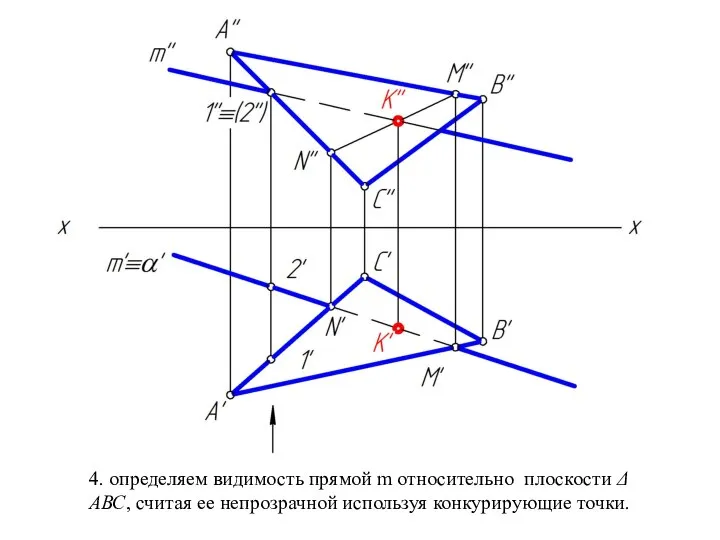
4. определяем видимость прямой m относительно плоскости Δ АВС, считая ее непрозрачной используя конкурирующие точки.