Содержание
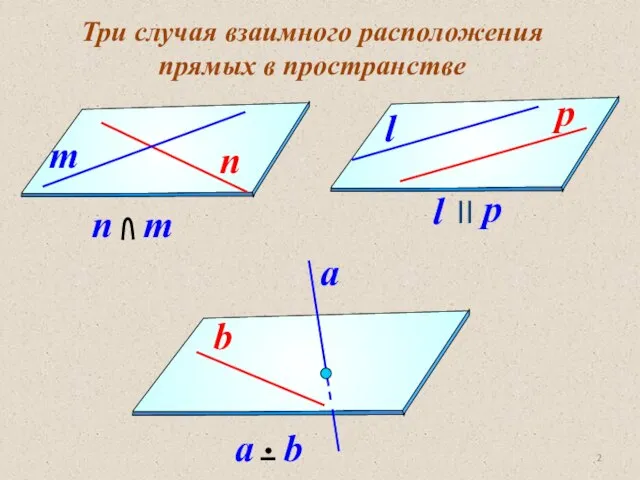
- 2. Три случая взаимного расположения прямых в пространстве
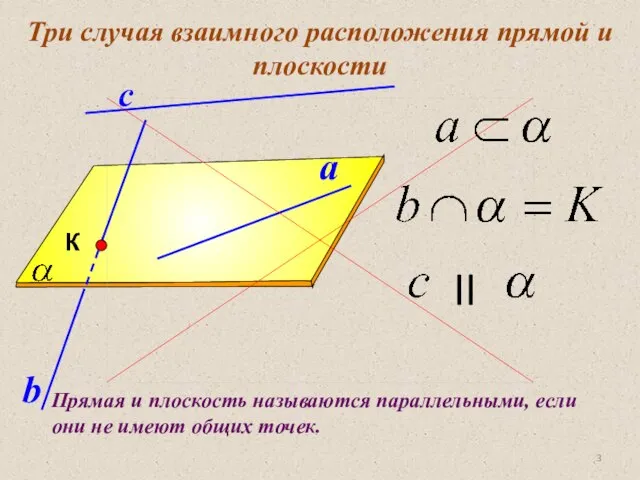
- 3. Три случая взаимного расположения прямой и плоскости Прямая и плоскость называются параллельными, если они не имеют
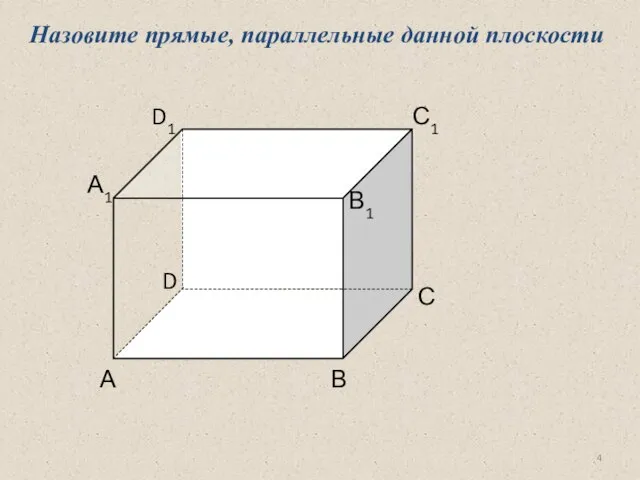
- 4. А В С D D1 С1 В1 А1 Назовите прямые, параллельные данной плоскости
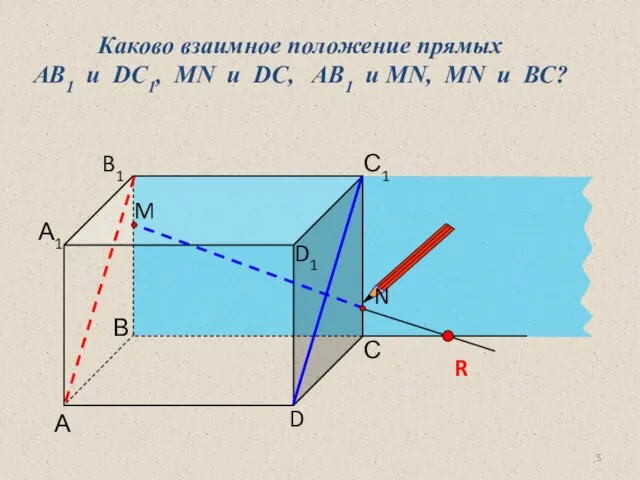
- 5. А D С В B1 С1 D1 А1 Каково взаимное положение прямых AB1 и DC1, МN
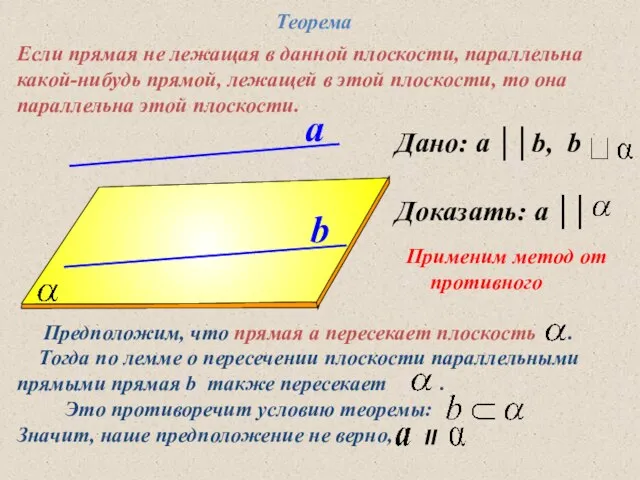
- 6. Дано: a ││b, b Доказать: a ││ a b Теорема Если прямая не лежащая в данной
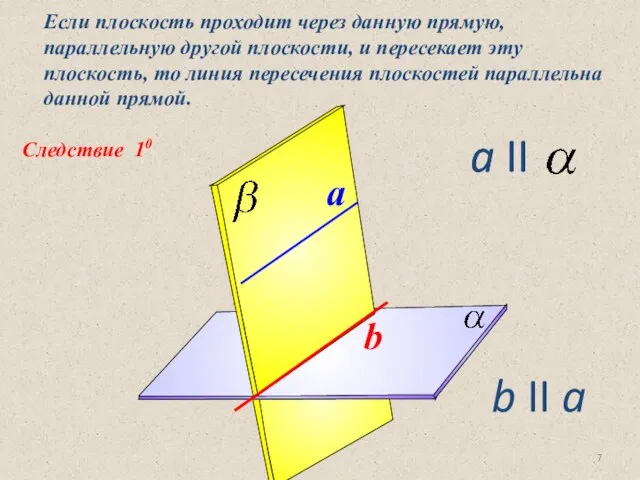
- 7. Следствие 10 Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то
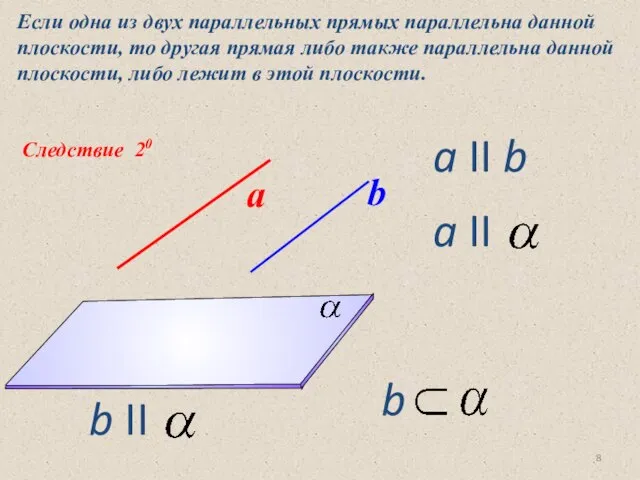
- 8. Следствие 20 Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также
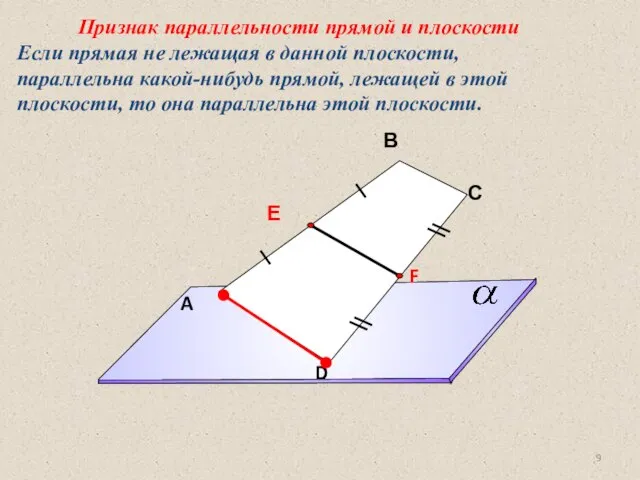
- 9. Признак параллельности прямой и плоскости Если прямая не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей
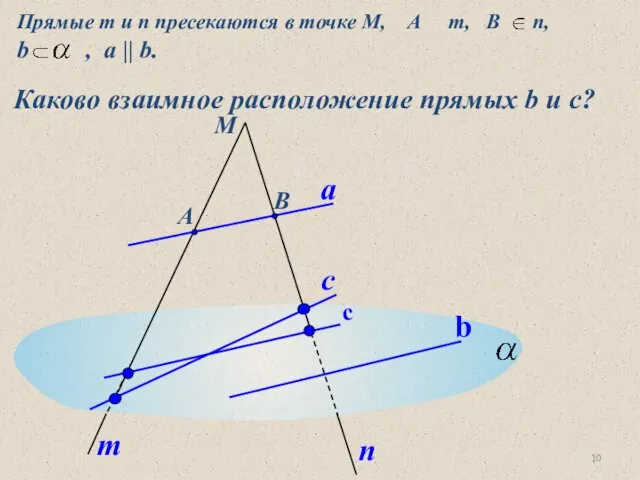
- 10. М А В b a m n Прямые m и n пресекаются в точке М, А
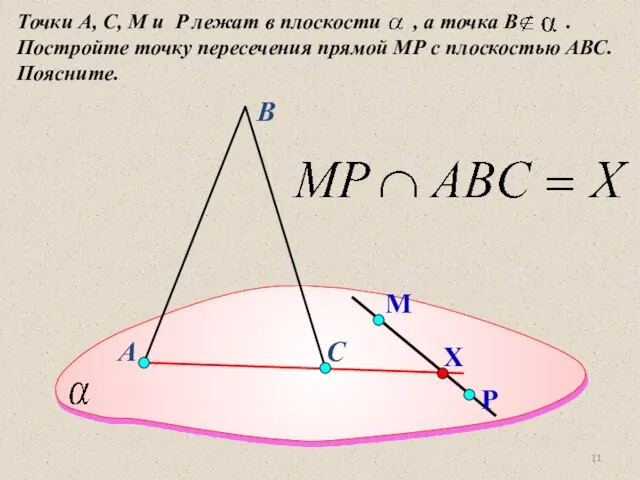
- 11. А Точки А, С, M и P лежат в плоскости , а точка В . Постройте
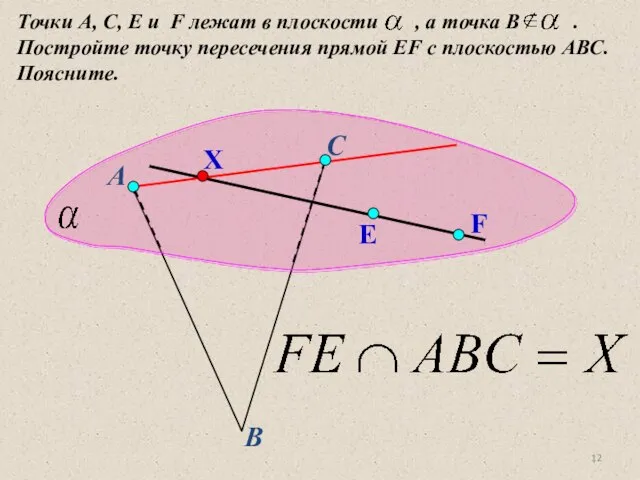
- 12. А В С E F
- 14. Скачать презентацию
 Геометрические портреты
Геометрические портреты Логарифм
Логарифм Множества. Операции над ними
Множества. Операции над ними Компьютерное моделирование процесса подготовки РКН к пуску. Лекция 15
Компьютерное моделирование процесса подготовки РКН к пуску. Лекция 15 Квадратичная функция
Квадратичная функция Презентация на тему Решаем задачи (1 класс)
Презентация на тему Решаем задачи (1 класс)  Интегривование тригонометрических функций
Интегривование тригонометрических функций Аппроксимация функций. Метод Лагранжа
Аппроксимация функций. Метод Лагранжа Презентация на тему Теория вероятностей и комбинаторные правила
Презентация на тему Теория вероятностей и комбинаторные правила  О математическом языке
О математическом языке Формулы сокращенного умножения. Интерактивный плакат
Формулы сокращенного умножения. Интерактивный плакат Графический диктант. Тема: Делимость чисел
Графический диктант. Тема: Делимость чисел Устный счёт
Устный счёт Площади и объемы
Площади и объемы Преобразование логарифмических выражений
Преобразование логарифмических выражений Решение задач по теме Арифметическая прогрессия
Решение задач по теме Арифметическая прогрессия Моделирование при управлении рисками авиапредприятий
Моделирование при управлении рисками авиапредприятий Методика изучения массы
Методика изучения массы Единицы измерения длины. Задания
Единицы измерения длины. Задания Показатели надежности электроснабжения
Показатели надежности электроснабжения Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений Больше, меньше, столько же
Больше, меньше, столько же Свойство противоположных сторон прямоугольника
Свойство противоположных сторон прямоугольника Санкт-Петербург на уроках математики
Санкт-Петербург на уроках математики formuly_privedenia
formuly_privedenia Решение уравнений. Буквенные выражения
Решение уравнений. Буквенные выражения Неопределённый интеграл
Неопределённый интеграл Формулы дифференцирования
Формулы дифференцирования