Слайд 3Неопределённый интеграл и его свойства.

Слайд 4Вообще, если F0(x)-первообразная f(x) на множестве X, то любая функция вида
F(X)=

F0(x)+C,
где С- произвольная константа, тоже будет первообразной f(х) на том же множестве X. F'(x)=(F0(x)+C)= F'0(х)+С= f(x\xeX.
Итак, мы можем сделать следующий вывод. Если какой-нибудь первообразной данной функции прибавить постоянное слагаемое, то снова получится первообразная той же функции.
Слайд 5Интегралы элементарных функций
Первообразные рациональных функций

Слайд 9Логарифмы
Основные интегралы с логарифмическими функциями





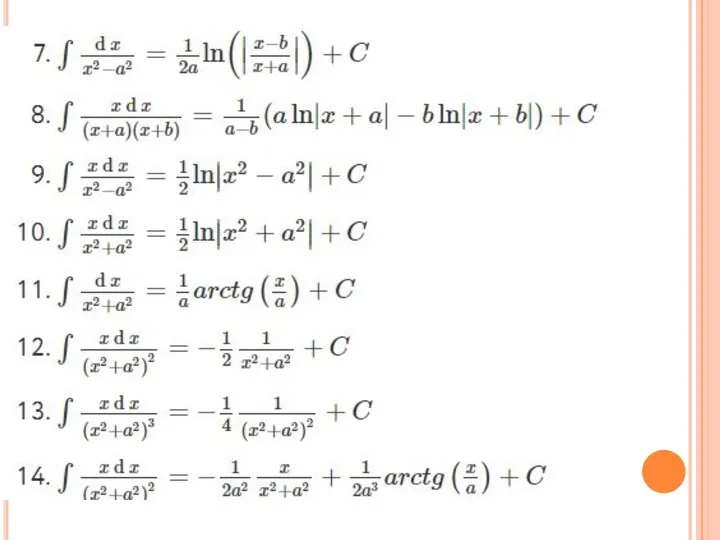

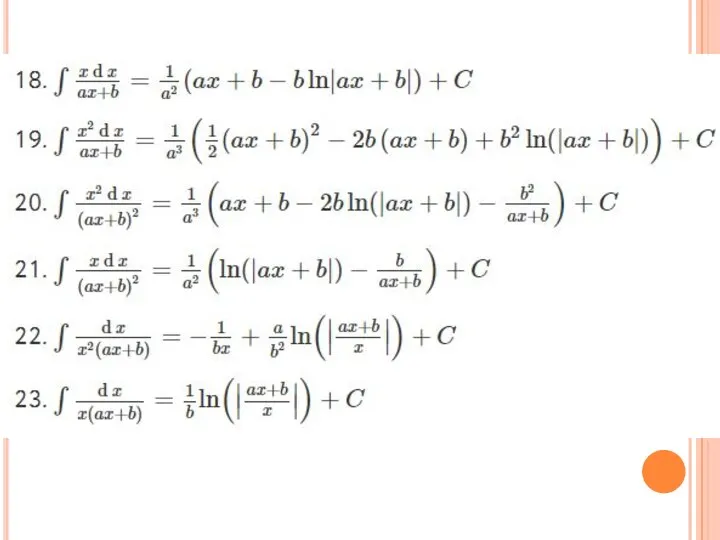

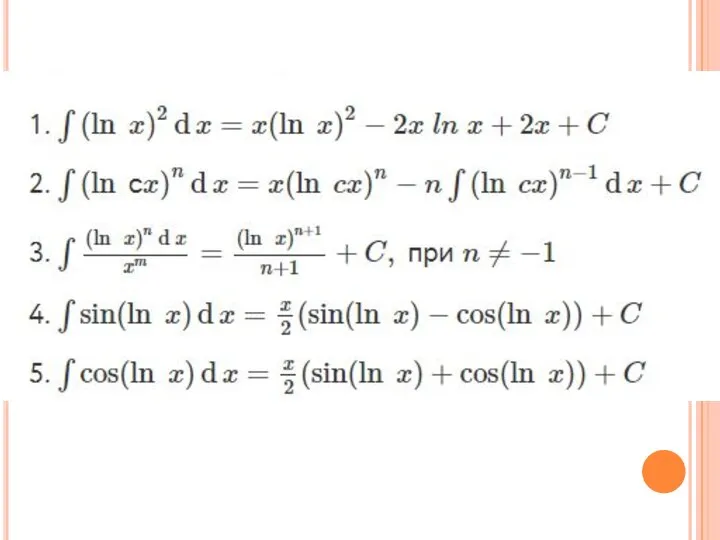



 Геометрическая мозаика из правильных одноимённых многоугольников
Геометрическая мозаика из правильных одноимённых многоугольников Предпосылки МНК для парной линейной регрессии. Тема 4
Предпосылки МНК для парной линейной регрессии. Тема 4 Задачи. Урок 20
Задачи. Урок 20 Понятие неравенство
Понятие неравенство Площадь полной поверхности пирамиды
Площадь полной поверхности пирамиды Преобразование простейших тригонометрических выражений
Преобразование простейших тригонометрических выражений Информационные технологии образовании
Информационные технологии образовании Множество
Множество Час занимательной математики
Час занимательной математики Занимательные задачи (4 класс)
Занимательные задачи (4 класс) Задача по математике (1 класс)
Задача по математике (1 класс) Приемы вычитания с переходом через разряд вида 35 - 7
Приемы вычитания с переходом через разряд вида 35 - 7 Площадь фигур
Площадь фигур Вычитание дроби из целого числа (урок 116)
Вычитание дроби из целого числа (урок 116) Построение сечения
Построение сечения Векторный анализ -теория поля. Типы векторных полей. Лекция 18
Векторный анализ -теория поля. Типы векторных полей. Лекция 18 ДПА 11 класс Первообразная и интеграл
ДПА 11 класс Первообразная и интеграл Треугольники и их виды
Треугольники и их виды Функция y = f(x)
Функция y = f(x) Миллиметр. В каких числах сумма цифр равна 5?
Миллиметр. В каких числах сумма цифр равна 5? Понятие производной
Понятие производной Позиционные задачи
Позиционные задачи Байесовский анализ и сети Байеса
Байесовский анализ и сети Байеса Степень с натуральным и целым показателем
Степень с натуральным и целым показателем Логарифмические неравенства. Решение заданий
Логарифмические неравенства. Решение заданий Мой кабинет – моя лаборатория Презентацию подготовила заведующая школьным кабинетом математики №14 Ларионова Татьяна Ивановна.
Мой кабинет – моя лаборатория Презентацию подготовила заведующая школьным кабинетом математики №14 Ларионова Татьяна Ивановна. Comparative of superlative
Comparative of superlative Натуральый степень, свойства, показатель
Натуральый степень, свойства, показатель