Содержание
- 2. Свойства функции
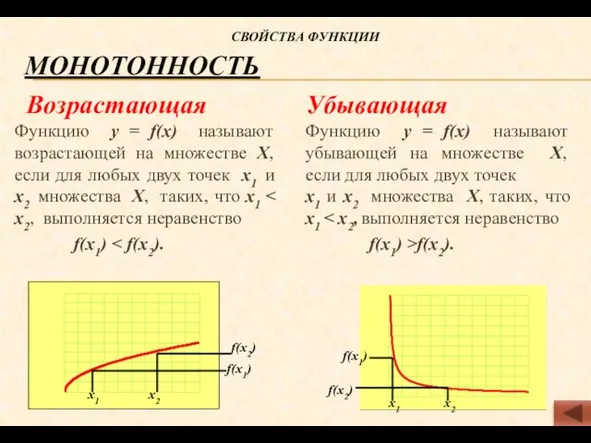
- 3. Монотонность Возрастающая Функцию у = f(х) называют возрастающей на множестве Х, если для любых двух точек
- 4. Наибольшее и наименьшее значения Число m называют наименьшим значением функции у = f(х) на множестве Х,
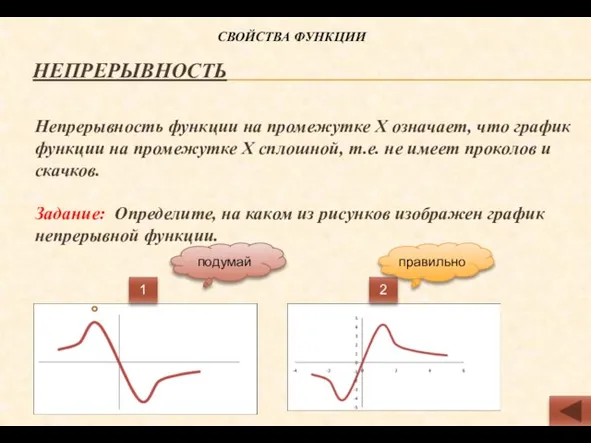
- 5. Непрерывность Непрерывность функции на промежутке Х означает, что график функции на промежутке Х сплошной, т.е. не
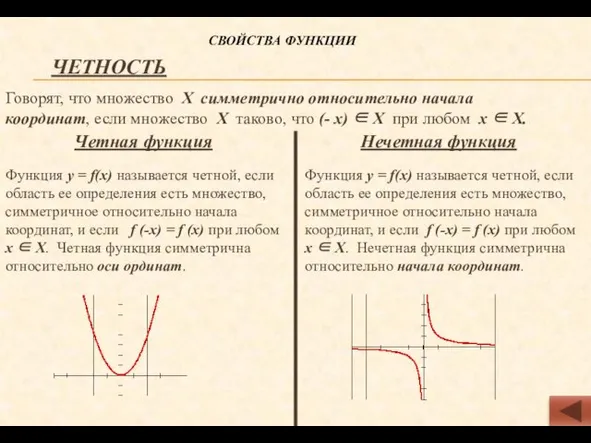
- 6. Свойства функции ЧЕТНОСТЬ Говорят, что множество Х симметрично относительно начала координат, если множество Х таково, что
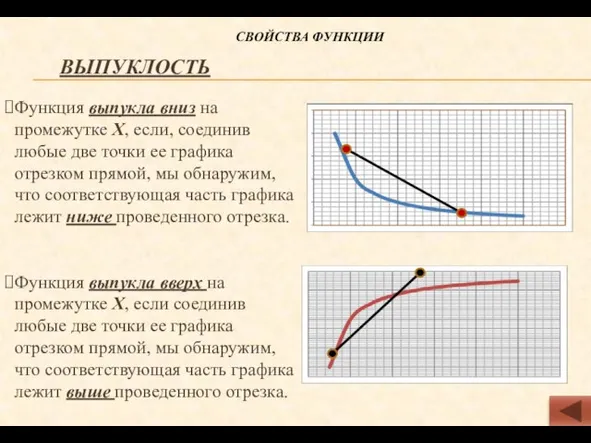
- 7. Выпуклость Функция выпукла вниз на промежутке Х, если, соединив любые две точки ее графика отрезком прямой,
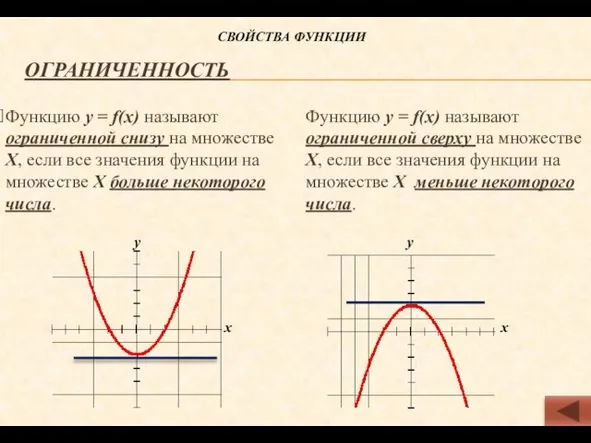
- 8. Ограниченность Функцию у = f(х) называют ограниченной снизу на множестве Х, если все значения функции на
- 9. Алгоритм описания свойств функций Область определения Область значений Четность Монотонность Непрерывность Ограниченность Наибольшее и наименьшее значения
- 10. Опишите свойства функций: у= kx + m – линейная функция у = kx2 – квадратичная функция
- 11. Свойства функции y = kx + m (k ≠ 0) D(f) = (-∞; +∞); E(f) =
- 12. при k D(f) = (-∞, +∞); Е(f) = (-∞, 0]; четная убывает на луче [0,+∞), возрастает
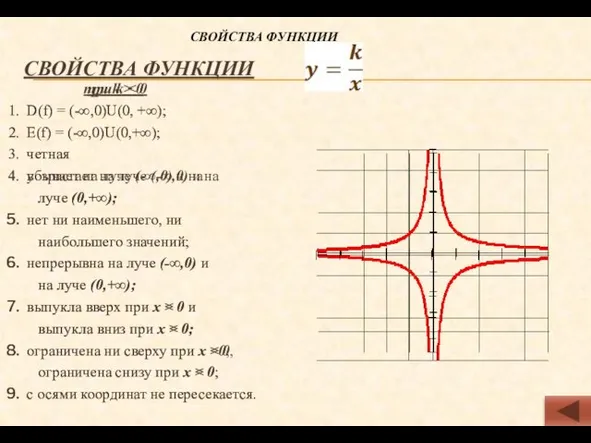
- 13. при k > 0 D(f) = (-∞,0)U(0, +∞); Е(f) = (-∞,0)U(0,+∞); четная убывает на луче (-∞,0)
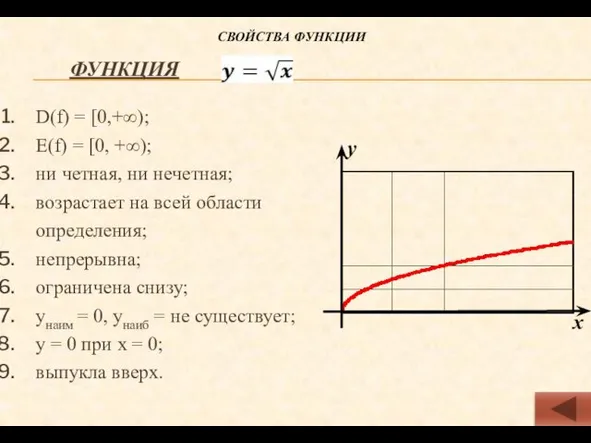
- 14. Функция D(f) = [0,+∞); Е(f) = [0, +∞); ни четная, ни нечетная; возрастает на всей области
- 15. Функция у = |х| D(f) = (-∞,+∞); Е(f) = [0, +∞); четная; убывает на луче (-∞,0],
- 17. Скачать презентацию





![при k D(f) = (-∞, +∞); Е(f) = (-∞, 0]; четная убывает](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/285990/slide-11.jpg)

 Умножение числа на 1
Умножение числа на 1 L_3
L_3 Аксонометрические проекции геометрических тел
Аксонометрические проекции геометрических тел Задачи о теплице. Пример решения
Задачи о теплице. Пример решения Второй признак равенства треугольников
Второй признак равенства треугольников ОГЭ 2020-2021. Задание №7
ОГЭ 2020-2021. Задание №7 Функции и их графики
Функции и их графики Приложения Определенного интеграла
Приложения Определенного интеграла Частота и вероятность случайного события
Частота и вероятность случайного события Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис
Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис Презентация на тему Математический диктант 2 класс
Презентация на тему Математический диктант 2 класс  Головоломки и занимательные задачи
Головоломки и занимательные задачи Иррациональные числа
Иррациональные числа Введение в стереометрию. Аксиомы стереометрии и некоторые следствия из аксиом. 10 класс
Введение в стереометрию. Аксиомы стереометрии и некоторые следствия из аксиом. 10 класс Решение примеров и задач с числами в пределах 10
Решение примеров и задач с числами в пределах 10 Математические компоненты вычитания
Математические компоненты вычитания Презентация на тему Устный счёт в пределах 10 (1 класс)
Презентация на тему Устный счёт в пределах 10 (1 класс)  Скалярное произведение векторов. Решение задач
Скалярное произведение векторов. Решение задач Занимательная математика
Занимательная математика Теорема Пифагора. Урок 27
Теорема Пифагора. Урок 27 Луч. Дополнительные лучи. 5 класс
Луч. Дополнительные лучи. 5 класс Решение задач на проценты. Концентрация
Решение задач на проценты. Концентрация Теория вероятности
Теория вероятности Прямые на плоскости. Задачи 6 и 7
Прямые на плоскости. Задачи 6 и 7 Число потоков в графе
Число потоков в графе Основы метрологии. Лекция 1
Основы метрологии. Лекция 1 Математика. Раздел 7. Функции и графики. Занятие 70. Схема исследования функции
Математика. Раздел 7. Функции и графики. Занятие 70. Схема исследования функции Тела вращения
Тела вращения