Содержание
- 2. Цели: 1) Рассмотреть теорему о точке пересечения высот и следствие из неё; 2) Формировать умения применять
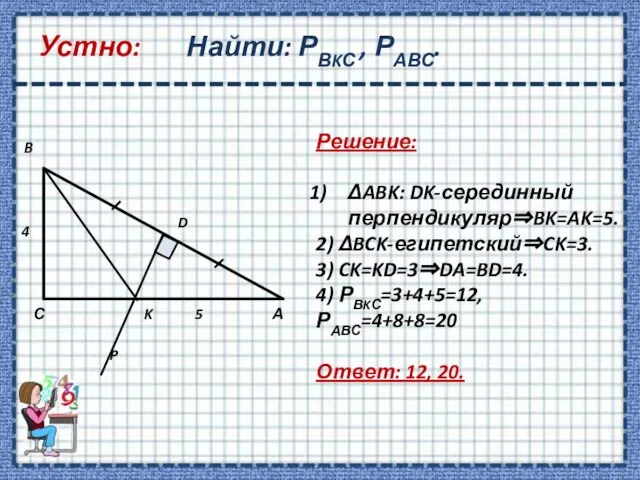
- 3. Устно: Найти: РВKС , РАВС. Решение: ΔABK: DK-серединный перпендикуляр⇒BK=AK=5. 2) ΔBCK-египетский⇒CK=3. 3) CK=KD=3⇒DA=BD=4. 4) РВKС=3+4+5=12, РАВС=4+8+8=20
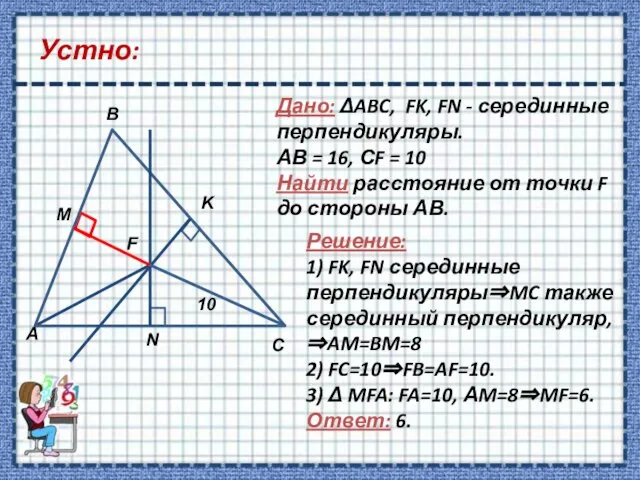
- 4. Устно: Дано: ΔABC, FK, FN - серединные перпендикуляры. АВ = 16, СF = 10 Найти расстояние
- 5. является самым могущественным средством для изощрения наших умственных способностей и даёт нам возможность правильно мыслить и
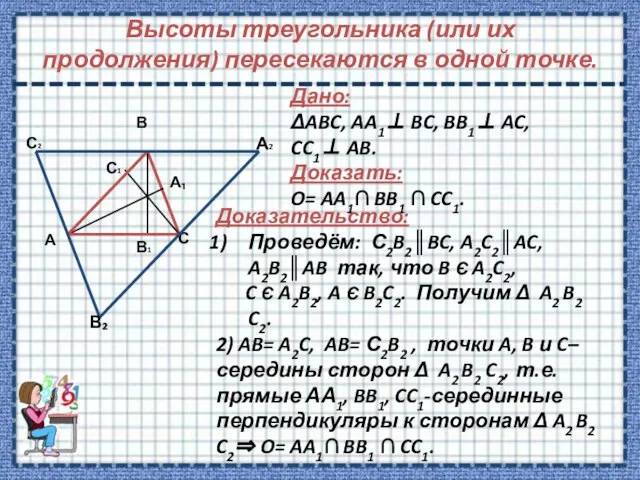
- 6. Высоты треугольника (или их продолжения) пересекаются в одной точке. Дано: ΔABC, AA1⊥ BC, BB1⊥ AC, CC1⊥
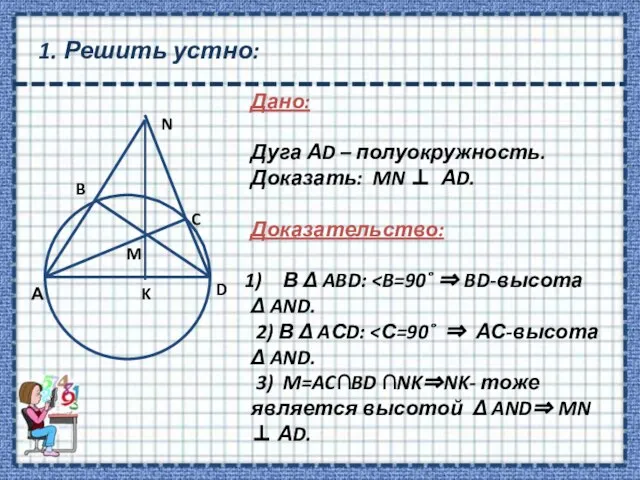
- 7. 1. Решить устно: Дано: Дуга АD – полуокружность. Доказать: MN ⊥ АD. Доказательство: В Δ ABD:
- 8. № 677. Доказательство: 1) 2) По теореме о биссектрисе угла точка О равноудалена от сторон АВ,
- 9. № 684 Доказательство: По свойству углов при основании равнобедренного треугольника Δ МАВ – равнобедренный, АМ =
- 11. Скачать презентацию




 Векторы на плоскости
Векторы на плоскости Четырехугольники
Четырехугольники Векторы. Действия с векторами
Векторы. Действия с векторами Презентация на тему Число и цифра 3. Состав числа 3 (1 класс)
Презентация на тему Число и цифра 3. Состав числа 3 (1 класс)  Замечательные точки и линии треугольника. 9 класс
Замечательные точки и линии треугольника. 9 класс Занимательная математика
Занимательная математика Линейная алгебра
Линейная алгебра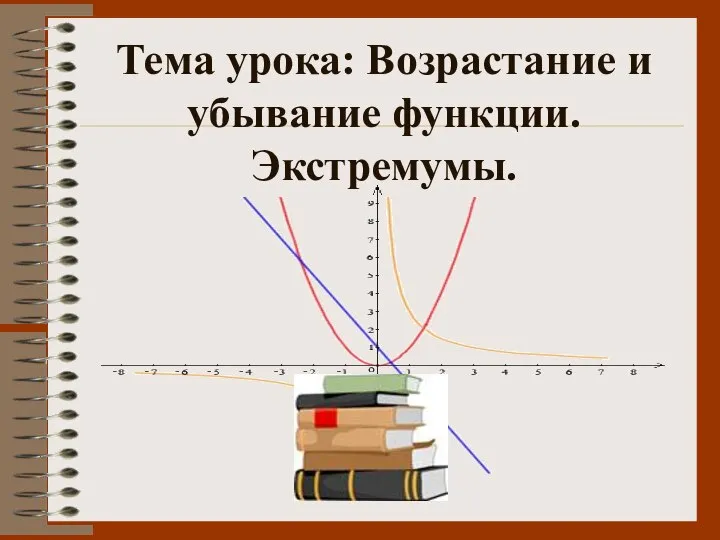 Монотонность функции
Монотонность функции Variācijas, permutācijas, kombinācijas
Variācijas, permutācijas, kombinācijas Математика на олимпийских играх. Керлинг. Разработка для учащихся 5 класса
Математика на олимпийских играх. Керлинг. Разработка для учащихся 5 класса Внутренний контроль качества результатов КХА
Внутренний контроль качества результатов КХА Треугольники. Часть 1
Треугольники. Часть 1 Дробные рациональные уравнения. Задания для интерактивной доски. 8 класс
Дробные рациональные уравнения. Задания для интерактивной доски. 8 класс Правильные многогранники
Правильные многогранники Презентация на тему Применение производной
Презентация на тему Применение производной  Элементы нелинейного функционального анализа. Гладкие многообразия. Два способа задания атласа на окружности
Элементы нелинейного функционального анализа. Гладкие многообразия. Два способа задания атласа на окружности Делаем математику видимой. Мяч из треугольников для квеста
Делаем математику видимой. Мяч из треугольников для квеста Матричная алгебра. Лекция 2
Матричная алгебра. Лекция 2 Задачи на нахождение расстояния между вершинами многогранника, все двугранные углы которого, прямые
Задачи на нахождение расстояния между вершинами многогранника, все двугранные углы которого, прямые 1-2_1
1-2_1 Треугольник. Подготовка к контрольной работе
Треугольник. Подготовка к контрольной работе Умножение для ленивых? 5 класс
Умножение для ленивых? 5 класс Плоская линия в R2
Плоская линия в R2 Действия с десятичными дробями. Интерактивный тренажёр
Действия с десятичными дробями. Интерактивный тренажёр Тест по теме функция
Тест по теме функция Применение комплексных чисел на практике
Применение комплексных чисел на практике Презентация на тему Уменьшаемое. Вычитаемое. Разность
Презентация на тему Уменьшаемое. Вычитаемое. Разность  Симметрия в искусстве
Симметрия в искусстве