Содержание
- 2. Для создания трехмерной анимации требуется не только разбираться в программном обеспечении, но и быть знатоком физики
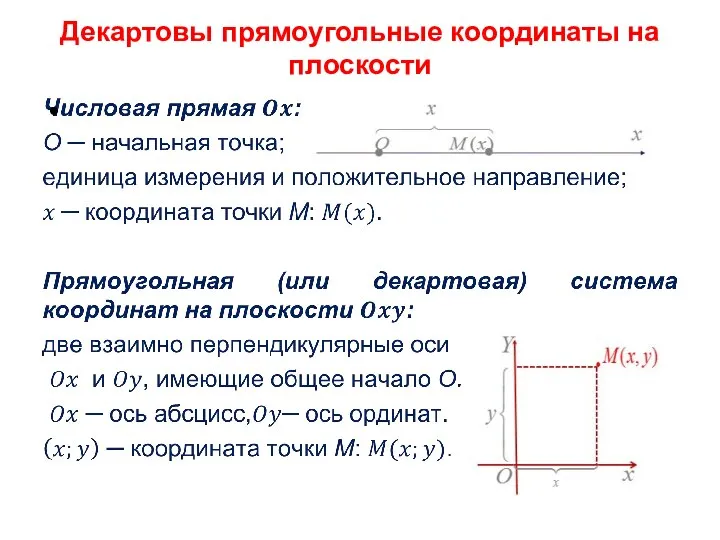
- 3. Декартовы прямоугольные координаты на плоскости
- 4. Декартовы прямоугольные координаты в пространстве
- 6. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ Длиной (или модулем) вектора называется длина отрезка АВ. Существует нуль- вектор: Два вектора
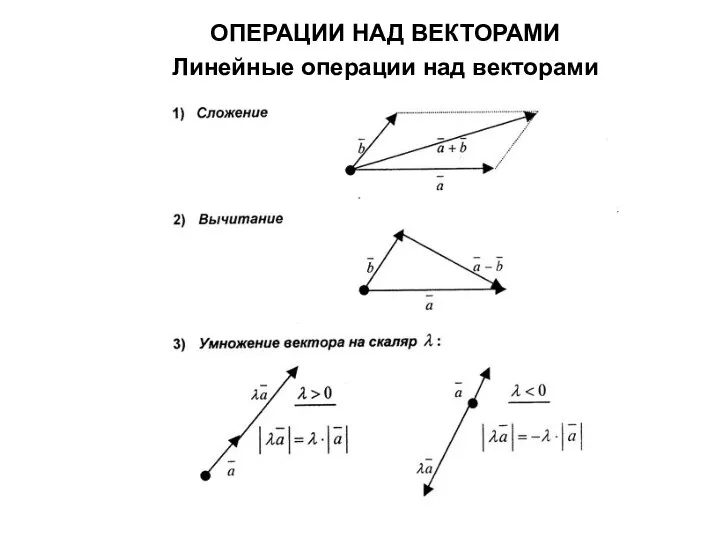
- 7. ОПЕРАЦИИ НАД ВЕКТОРАМИ Линейные операции над векторами
- 10. Направляющие косинусы
- 11. Операции над векторами, заданными своими координатами Пример.
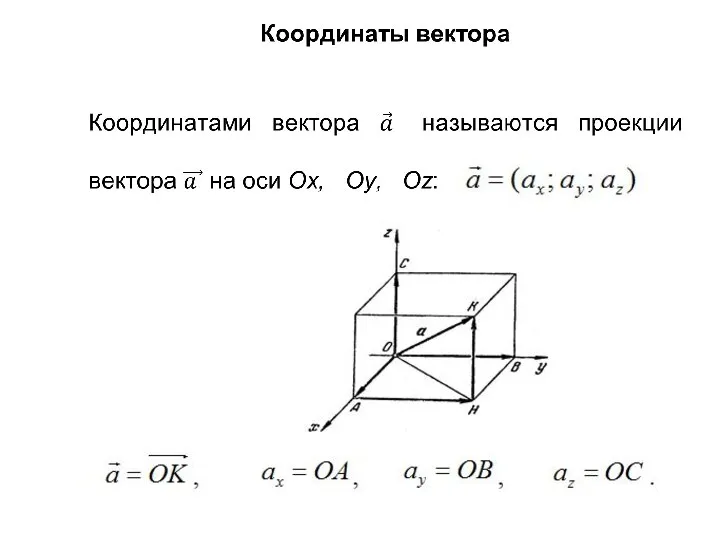
- 12. Разложение вектора по ортам Орты – единичные векторы осей Ox, Oy, Oz. Тогда
- 13. Скалярное произведение
- 14. Свойства скалярного произведения 1. 2. 3. 4. угол между двумя векторами
- 15. Коллинеарность и перпендикулярность векторов Векторы коллинеарные тогда и только тогда, когда координаты пропорциональны: Векторы перпендикулярные тогда
- 16. Пример Даны векторы : Найти:
- 17. Решение По определению Найдем длины векторов и . По формуле найдем Скалярный квадрат равен квадрату модуля
- 18. Скалярное произведение Угол между векторами определяется равенством: Откуда
- 19. Разложение вектора Задача: разложить вектор по векторам и . Решение. Найдем числа α и β, удовлетворяющие
- 20. Матрицы второго и третьего порядка Квадратной матрицей второго порядка называется таблица чисел: содержащая две строки и
- 21. Определитель второго порядка
- 22. Определитель третьего порядка Определителем квадратной матрицы А третьего порядка или− определителем третьего порядка) называется число, обозначаемое:
- 23. Определитель третьего порядка. Пример 1. Вычислить определитель: Решение:
- 24. Разложения определителя по элементам любой строки (столбца) матрицы
- 25. Разложение определителя третьего порядка по элементам второй строки Например, выбрав для разложения вторую строку определителя, получим
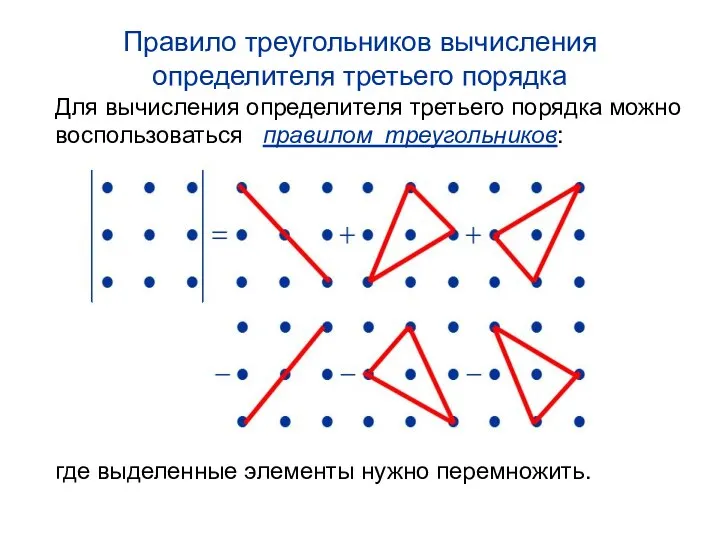
- 26. Правило треугольников вычисления определителя третьего порядка Для вычисления определителя третьего порядка можно воспользоваться правилом треугольников: где
- 27. Пример правила треугольников вычисления определителя третьего порядка Вычислить определитель: Решение.
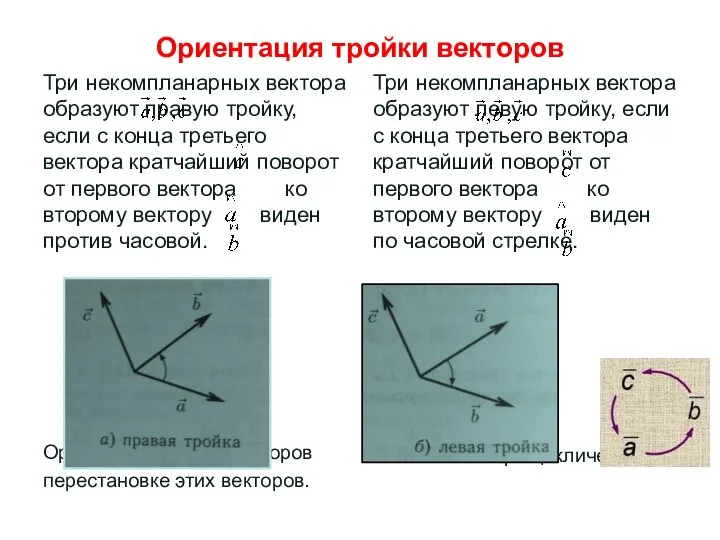
- 28. Ориентация тройки векторов Три некомпланарных вектора образуют правую тройку, если с конца третьего вектора кратчайший поворот
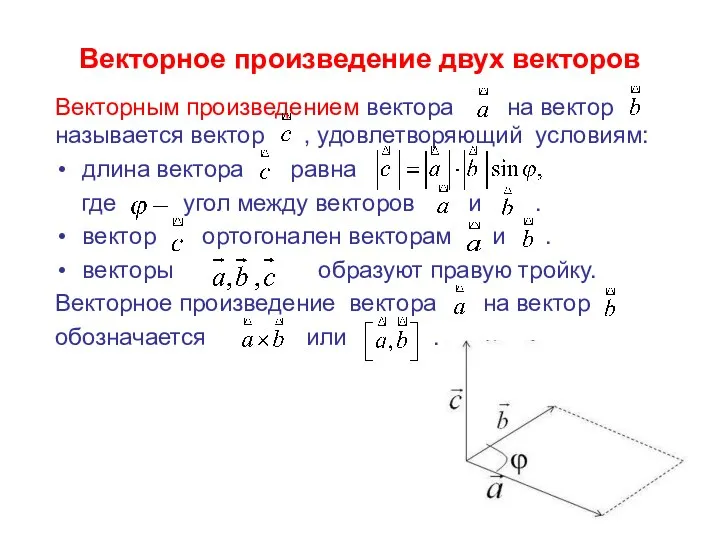
- 29. Векторное произведение двух векторов Векторным произведением вектора на вектор называется вектор , удовлетворяющий условиям: длина вектора
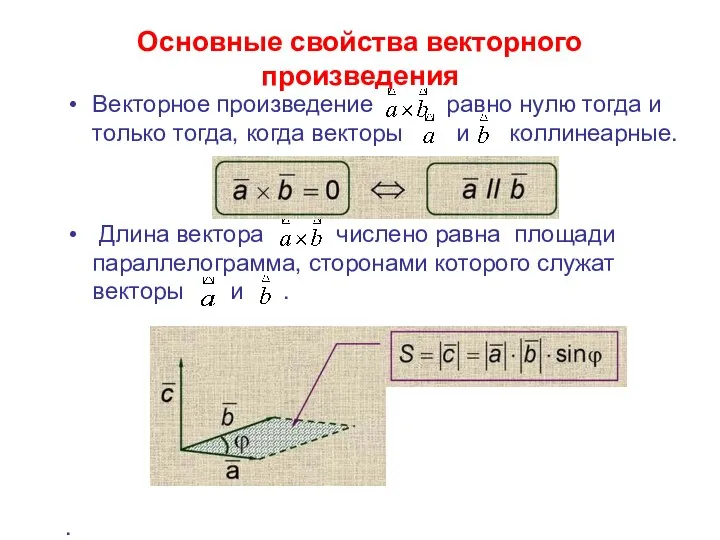
- 30. Основные свойства векторного произведения Векторное произведение равно нулю тогда и только тогда, когда векторы и коллинеарные.
- 31. Законы векторного произведения .
- 32. Выражение векторного произведение через прямоугольные координаты Пусть Oxyz - прямоугольная система координат, орты координатных осей этой
- 33. Пример применения в геометрии векторного произведения .
- 34. Смешанное произведение трех векторов Смешанным произведением трех векторов , и называется число, обозначаемое , равное скалярному
- 35. Компланарные векторы Три вектора называются компланарными , если они лежат на одной плоскости или на параллельных
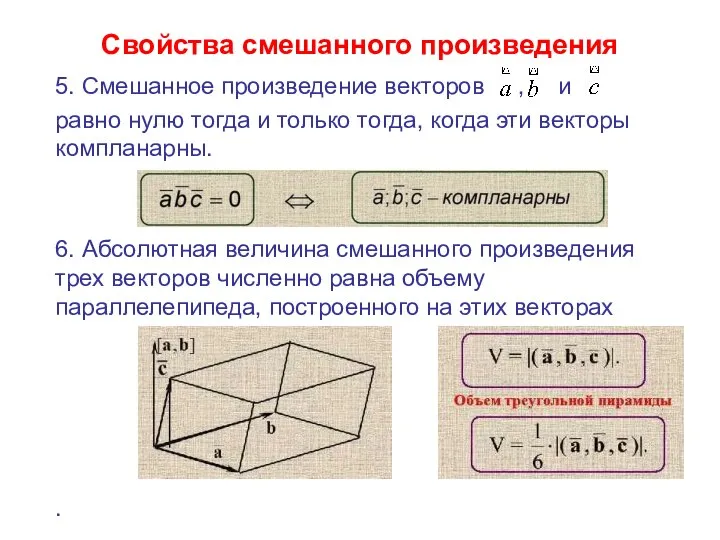
- 36. Свойства смешанного произведения 5. Смешанное произведение векторов , и равно нулю тогда и только тогда, когда
- 37. Выражение смешанного произведения через координаты векторов .
- 39. Скачать презентацию




























 Части множества
Части множества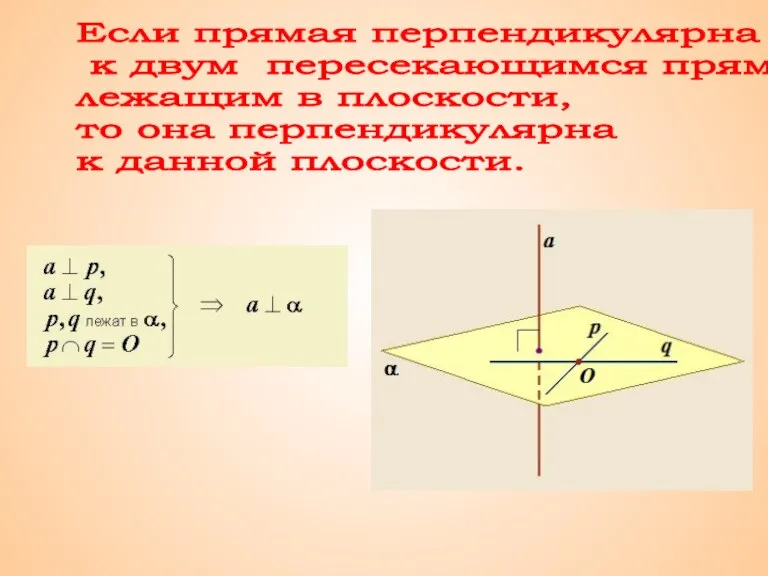 Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Разделение переменных в уравнении Лапласа в сферических координатах. Сферические и шаровые функции Лапласа
Разделение переменных в уравнении Лапласа в сферических координатах. Сферические и шаровые функции Лапласа LP (1)
LP (1) Векторный анализ и уравнения Максвелла
Векторный анализ и уравнения Максвелла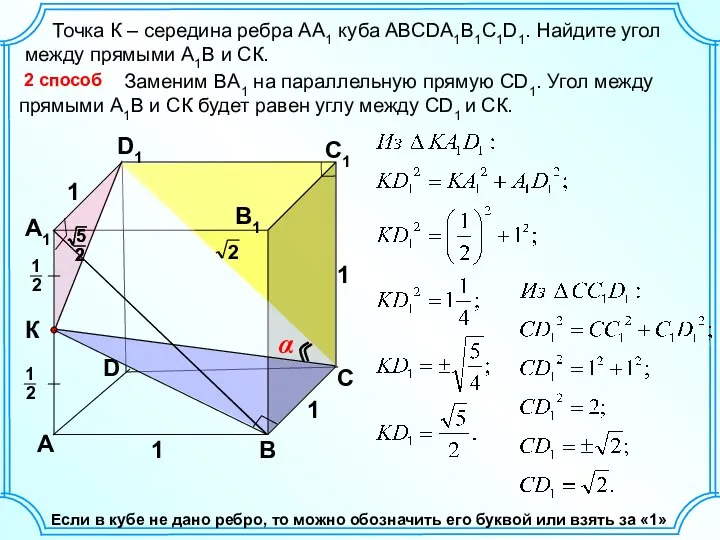 Решение задач
Решение задач Графический метод решения систем уравнений
Графический метод решения систем уравнений Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Числові нерівності. Властивості числових нерівностей
Числові нерівності. Властивості числових нерівностей Кривая Коха. Дробная размерность. Метод L-систем
Кривая Коха. Дробная размерность. Метод L-систем Национальный стандарт по библиотечной статистике: преемственность и новые подходы
Национальный стандарт по библиотечной статистике: преемственность и новые подходы Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Повторение курса алгебры (7 класс)
Повторение курса алгебры (7 класс) Литература
Литература Решение задач
Решение задач Квадратный корень
Квадратный корень Показательные уравнения
Показательные уравнения Решение уравнений и построение точек по их координатам. 6 класс
Решение уравнений и построение точек по их координатам. 6 класс Бумажные складные модели и их использование на уроках геометрии
Бумажные складные модели и их использование на уроках геометрии Сложение вида +4
Сложение вида +4 Арифметические действия
Арифметические действия Дискретная математика. Задание №2. Матрица инцидентности неориентированного графа
Дискретная математика. Задание №2. Матрица инцидентности неориентированного графа Обыкновенные дроби
Обыкновенные дроби Выполнение плана чертежа в масштабе
Выполнение плана чертежа в масштабе Дифференциальные уравнения 1-го порядка
Дифференциальные уравнения 1-го порядка Доминино
Доминино Соста числа 11
Соста числа 11 Урок начинается. Занимательная математика
Урок начинается. Занимательная математика