Содержание
- 2. Функцию у = f ( x), где х ∊ Х, называют периодической, если существует Т ≠
- 3. sin ( x – 2π) = sin x = sin ( x + 2π); cos (
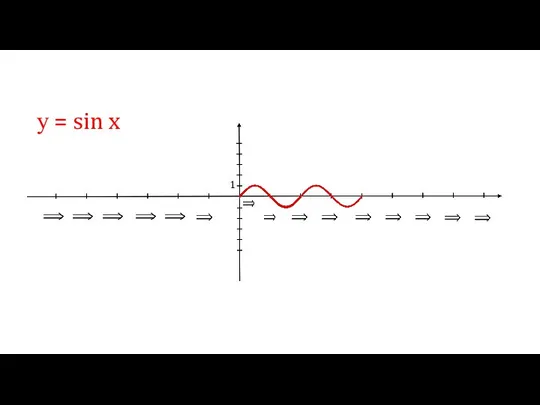
- 4. у = sin x 1
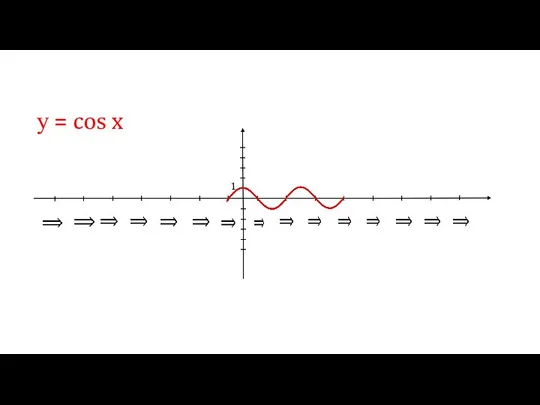
- 5. у = cos x 1
- 6. Для построения графика периодической функции с периодом Т нужно: 1. Построить ветвь графика на любом промежутке
- 8. Пример 1. Найти основной период функции у = сos5x. Решение. Пусть Т – основной период функции
- 9. Решение. ⇒ ⇒ ⇒
- 11. Скачать презентацию






 Процент. Сорауларга җавап бирегез
Процент. Сорауларга җавап бирегез Масса. Весы
Масса. Весы Колесо истории математики
Колесо истории математики Одиниці вимірювання часу
Одиниці вимірювання часу Третий признак равенства треугольников. 7 класс
Третий признак равенства треугольников. 7 класс Предел функции в точке
Предел функции в точке Сложение и вычитание трехзначных чисел
Сложение и вычитание трехзначных чисел Решение задач по теме: Параллелограмм (1)
Решение задач по теме: Параллелограмм (1) Понятие производной
Понятие производной Математический тренажер
Математический тренажер Полином Жегалкина
Полином Жегалкина Презентация на тему Производная
Презентация на тему Производная  Возведение в степень произведения. 7 класс
Возведение в степень произведения. 7 класс Презентация на тему Прикладные задачи на экстремумы
Презентация на тему Прикладные задачи на экстремумы  Устный счёт. Назови числа по порядку
Устный счёт. Назови числа по порядку Признаки равенства треугольников
Признаки равенства треугольников Электронное приложение к рабочей тетради по математике 1 класс школа VIII вида дочисловой период
Электронное приложение к рабочей тетради по математике 1 класс школа VIII вида дочисловой период Готовимся к ЕГЭ
Готовимся к ЕГЭ Устный счет
Устный счет Арифметическая прогрессия
Арифметическая прогрессия Система уравнений. Метод алгебраического сложения
Система уравнений. Метод алгебраического сложения Теория Графов
Теория Графов Взаимное расположение прямой и окружност
Взаимное расположение прямой и окружност Линейная алгебра
Линейная алгебра Неравенства. Решить систему неравенств
Неравенства. Решить систему неравенств Ортогональная проекция плоской фигуры на плоскость и ее площадь
Ортогональная проекция плоской фигуры на плоскость и ее площадь Координатный луч
Координатный луч Целое уравнение и его корни
Целое уравнение и его корни