Слайд 2Какая система уравнений называется совместной?
Система уравнений называется совместной, если она имеет

по крайней мере одно решение.
Слайд 3Какая система уравнений несовместна?
Система уравнений несовместна, если она не имеет

решений.
Слайд 4Какие системы называются эквивалентными?
Две системы уравнений называются эквивалентными, если они

обе несовместны или обе совместны и имеют одни и те же решения.
Слайд 5Назовите элементарные преобразования системы.
перестановка местами уравнений системы;
умножение любого уравнения системы на число,

не равное нулю;
прибавление к одному уравнению системы другого, умноженного на число.
Слайд 6Гаусс Карл Фридрих (1777 - 1855)
Выдающийся немецкий математик. Его труды

глубоко повлияли на развитие математической мысли, которая была неизменной многие столетия. Гаусс занимался основной теоремой алгебры о количестве корней алгебраического уравнения.
Слайд 7Метод Гаусса
Это метод последовательного исключения переменных, когда с помощью элементарных преобразований

система уравнений приводится к эквивалентной системе ступенчатого (или треугольного) вида (прямой ход), из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные (обратный ход).







 Презентация на тему Теорема Виета
Презентация на тему Теорема Виета  Специальные случайные распределения, используемые в математической статистике
Специальные случайные распределения, используемые в математической статистике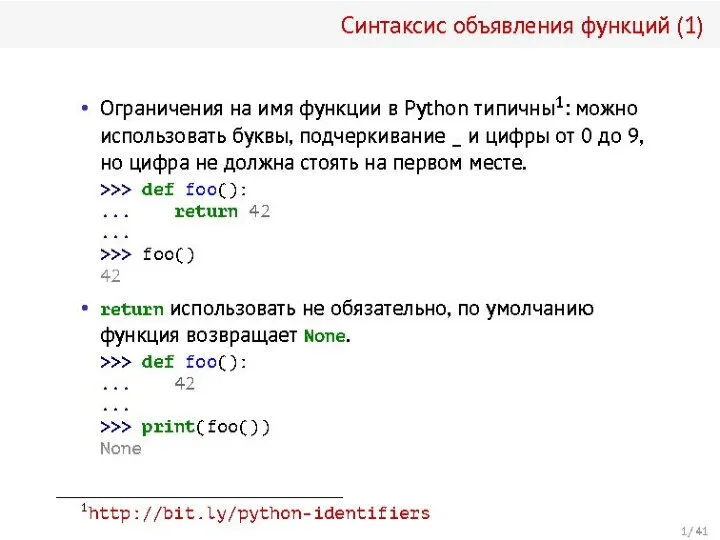 Синтаксис объявления функции
Синтаксис объявления функции Построение сечения многогранника плоскостью
Построение сечения многогранника плоскостью Ромб. Свойства ромба
Ромб. Свойства ромба Виды уравнений и способы их решения
Виды уравнений и способы их решения Биометрия, как наука
Биометрия, как наука Статистический анализ случайных погрешностей
Статистический анализ случайных погрешностей Неопределённый интеграл
Неопределённый интеграл Единицы измерений
Единицы измерений Метрология. Основные понятия
Метрология. Основные понятия Решение задач. 10 класс
Решение задач. 10 класс Площадь круга и секторов
Площадь круга и секторов Применение графов
Применение графов Координаты вектора
Координаты вектора Математика без границ. Конкурс
Математика без границ. Конкурс Приближенные вычисления
Приближенные вычисления Умножение и деление отрицательных чисел. Урок-путешествие
Умножение и деление отрицательных чисел. Урок-путешествие Презентация к уроку математики 6 класса учителя математики НОУ СОШ «Азъ Буки Веди» Ивахненко Натальи Геннадьевны
Презентация к уроку математики 6 класса учителя математики НОУ СОШ «Азъ Буки Веди» Ивахненко Натальи Геннадьевны Линейные пространства и подпространства
Линейные пространства и подпространства Нахождение угла между прямой и плоскостью
Нахождение угла между прямой и плоскостью Проверка статистических гипотез. Критерий согласия Пирсона (хи-квадрат)
Проверка статистических гипотез. Критерий согласия Пирсона (хи-квадрат) 08.09
08.09 Теория вероятностей. Вычисление вероятности выигрыша
Теория вероятностей. Вычисление вероятности выигрыша Коэффициенты линейной функции
Коэффициенты линейной функции Умножение натуральных чисел
Умножение натуральных чисел Вторая производная и ее физический смысл
Вторая производная и ее физический смысл Презентация на тему Сложение чисел с разными знаками (6 класс)
Презентация на тему Сложение чисел с разными знаками (6 класс)