Математика. Лекция 1

Использование математики в медицине
создание растворов требуемой концентрации
расчет дозы и графика приема лекарства
статистическая обработка медицинских данных
доказательная медицина
прогнозирование и планирование в медицине
расчет протезов и имплантов
разработка медицинских приборов
моделирование биологических процессов
изучение структуры макромолекул и т.д.
2

История создания математического анализа (17 век)
Математический анализ – раздел математики, объединяющий в себе дифференциальное и интегральное исчисление.
3
Готфрид Вильгельм Лейбниц
Основу математического анализа в конце XVII века заложили Лейбниц и его ученики (Бернулли, Лопиталь).
Они изучают свойства функций и бесконечно малых величин, вводят понятие производной, интеграла и дифференциала.

История создания математического анализа (18 век)
4
Исаак Ньютон
В 1708 году вспыхнул печально известный спор Лейбница с Ньютоном о научном приоритете открытия дифференциального исчисления, который независимо от него разработал основы математического анализа и использовал производную функции и дифференциальные уравнения
для описания движения планет и решения ряда других задач механики и гидравлики.

История создания математического анализа (18 век)
5
Леонард Эйлер
Последующее развитие математического анализа связано
с именем Эйлера. К его основным достижениям можно отнести использование бесконечно больших величин, нахождение способа разложения функций в бесконечные ряды, он ввел число e ≈ 2.718, мнимую единицу i в теории
комплексных чисел, разработал многочисленные приемы интегрирования, основы теории графов.

Дальнейшее развитие математического анализа (18-19 века)
6
Вариационное исчисление, поиск экстремума, интерполяция функций; определение предела; дифференциальные уравнения в частных производных; преобразование Фурье; теория чисел …
Жозеф Луи
Лагранж
Огюстен Луи
Коши
Карл Вейерштрасс
Софья
Ковалевская

I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
7
Def Дифференциальное исчисление - раздел математического анализа, в котором изучаются понятия производной и дифференциала и способы их применения к исследованию функций.
Def Производная функции - это предел отношения приращения функции к соответствующему бесконечно малому приращению ее аргумента.

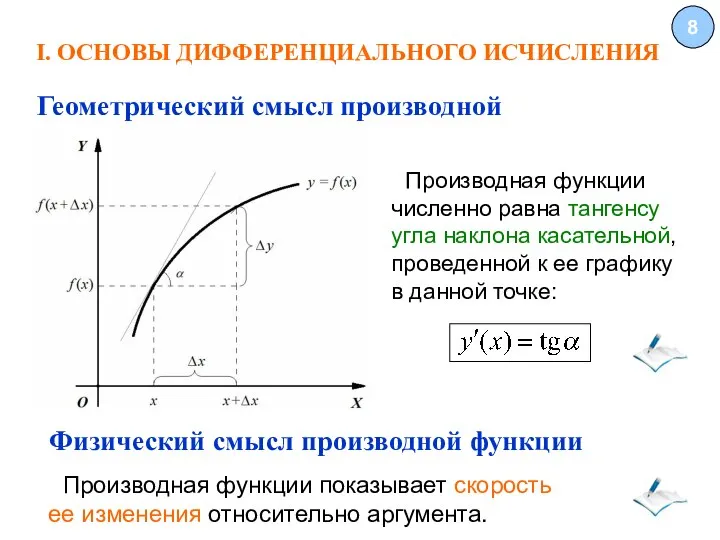
I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
8
Геометрический смысл производной
Производная функции численно равна тангенсу угла наклона касательной, проведенной к ее графику в данной точке:
Физический смысл производной функции
Производная функции показывает скорость
ее изменения относительно аргумента.

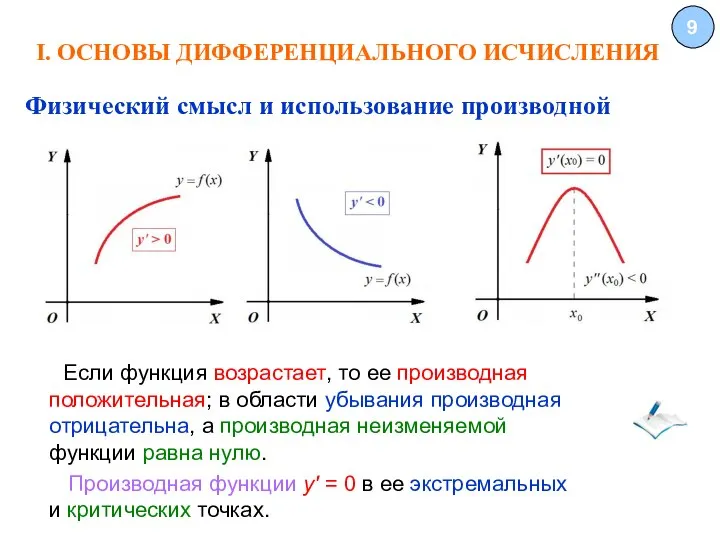
I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
9
Если функция возрастает, то ее производная положительная; в области убывания производная отрицательна, а производная неизменяемой
функции равна нулю.
Производная функции y′ = 0 в ее экстремальных
и критических точках.
Физический смысл и использование производной

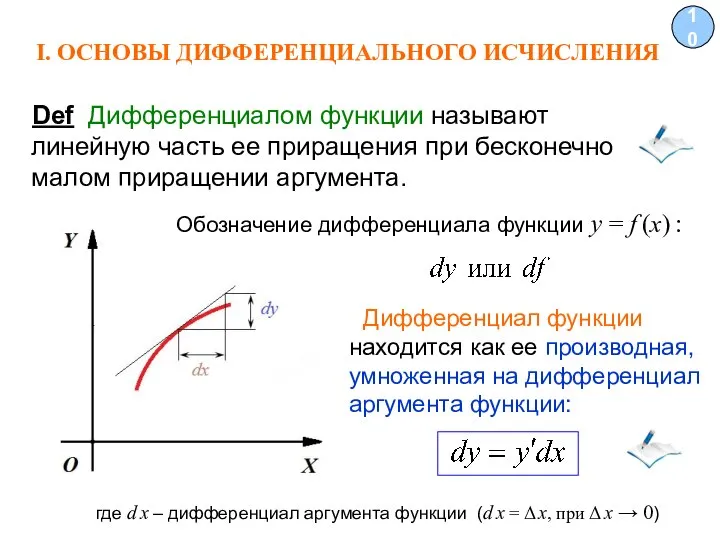
I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
10
Def Дифференциалом функции называют линейную часть ее приращения при бесконечно малом приращении аргумента.
Обозначение дифференциала функции y = f (x) :
Дифференциал функции находится как ее производная, умноженная на дифференциал аргумента функции:
где d x – дифференциал аргумента функции (d x = Δ x, при Δ x → 0)

I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
11
Таблица производных простейших функций

I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
12
Важные частные случаи:
Некоторые полезные формулы:

I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
13
Правила дифференцирования
где C – число, а u, v, f, g – некоторые функции

I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
14
Пример нахождения производной сложной функции:

I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
15
Пример нахождения производной сложной функции:

II. ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
16
Def Первообразной функции f(x) называется некоторая функция F(x), производная от которой равна исходной функции f(x), т.е.
Например, функция F(x) = x – sinx, является первообразной для функции f(x) = 1 – cosx.
Действительно, F′(x) = (x – sinx)′ = 1 – cosx = f(x).
Но функция F(x) = x – sinx + 5 также есть первообразная исходной функции: F′(x) = (x – sinx + 5)′ = 1 – cosx + 0 = f(x).
Таким образом, любая функция имеет бесконечное множество первообразных, отличающихся друг от друга на некоторую постоянную величину.

II. ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
17
Def Неопределенным интегралом функции называется множество всех ее первообразных.
Обозначение: Операция нахождения интеграла некоторой функции называется ее интегрированием. Интегрирование обратно дифференцированию (нахождению дифференциала), т.к.
где f(x) – подынтегральная функция, dx – дифференциал
ее аргумента, F(x) – ее первообразная, C = const.

II. ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
18
Основные правила интегрирования
где A – число, а f и g – некоторые функции.
Обратите внимание на то, что число A должно быть снаружи
подынтегральной функции, а не в ее аргументе!
Кроме того, формул для вычисления интегралов, аналогичным формулам «производная от произведения или частного»
не существует!

II. ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
19
Таблица интегралов простейших функций

II. ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
20
Def Определенным интегралом функции на
отрезке называется число, численно равное
разности ее первообразных на концах этого отрезка.
– формула Ньютона-Лейбница
где f(x) – подынтегральная функция, dx – дифференциал
ее аргумента, F(x) – ее первообразная; a, b – соответственно верхний и нижний пределы интегрирования.
Обратите внимание, что в формуле Ньютона-Лейбница сначала находится первообразная от верхнего предела интегрирования,
а затем от нижнего!

II. ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
21
Определенный интеграл функции на отрезке численно равен площади криволинейной трапеции, ограниченной графиком подынтегральной функции
и осью абсцисс, а также вертикальными прямыми, соответствующими пределам интегрирования.
Геометрический смысл определенного интеграла
Также определенные интегралы можно использовать для нахождения длин кривых, объемов тел; пути, пройденного телом;
работы переменной силы, центра тяжести тела, моментов инерции и т.д.

II. ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
22
Примеры:
Метод замены переменной (метод подстановки)

II. ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
23
Примеры:
Метод замены переменной (метод подстановки)

II. ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
24
Примеры:
Метод интегрирование по частям

III. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
25
Def Дифференциальным уравнением (ДУ) называется уравнение, содержащее неизвестную функцию и ее производные, т.е. уравнение вида
Наивысшая степень (тип) производной называется порядком дифф. ур-я. Решить ДУ значит найти неизвестную функцию y(x).
Дифференциальные уравнения возникают при решении различных задач физики, биологии, химии, экономики, медицины.
Для решения таких ур-й применяется операция интегрирования.
В общем случае ДУ имеет множество решений, отличающихся на некоторую постоянную величину (общее решение). Если же заданы начальные условия, то можно найти частное решение.

II. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
26
1) Свободные колебания грузика
на пружине:
Примеры задач, приводящих к ДУ
2) Изменение концентрации вещества в химической реакции:
A + B → C
3) Размножение бактерий (распространение слухов):

II. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
27
Метод решения ДУ 1-го порядка
с разделяющимися переменными
1) Переносим слагаемые, не
содержащие производную вправо:
2) Заменяем производную через
отношение дифференциалов:
3) Разделяем переменные
(множители с y – налево,
множители с x – направо):
4) Интегрируем обе части полученного уравнения, находим общее решение:

II. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
28
Примеры решения ДУ с разделяющимися переменными
1) Найти общее решение дифференциального уравнения
– общее решение в явном виде
Проверка:

II. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
29
Примеры решения ДУ с разделяющимися переменными
2) Найти частное решение дифференциального уравнения

II. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
30
Примеры решения ДУ с разделяющимися переменными
3) В начальный момент времени в чашке Петри было 10 бактерий. Сколько их станет при поддержании благоприятных условий через 1 час, если деления происходят в среднем через каждые 20 минут.
Данный процесс описывает ДУ
Постоянная деления
Скорость размножения бактерий пропорциональна их количеству. За небольшой промежуток времени Δt их количество возрастет на величину

II. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
31
Примеры решения ДУ с разделяющимися переменными
Через 1 час (60 мин) в чашке Петри будет около
бактерий.
Ответ: 200 бактерий.

ВЫВОДЫ:
рассмотрены основы дифференциального
и интегрального исчисления
показаны его некоторые возможности для решения теоретических и практических задач.
Литература
Лобоцкая Н.Л. Основы высшей математики.
Тимонюк В.А. Биофизика.
Ремизов А.Н. Медицинская и биологическая физика.
Чалий О.В. Медична і біологічна фізика.