Перпендикуляр и наклонная к прямой

Перпендикуляр
Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной к данной, от заданной точки до точки пересечения этих прямых.
АН-перпендикуляр к а
Н-основание перпендикуляра
А
Н
а

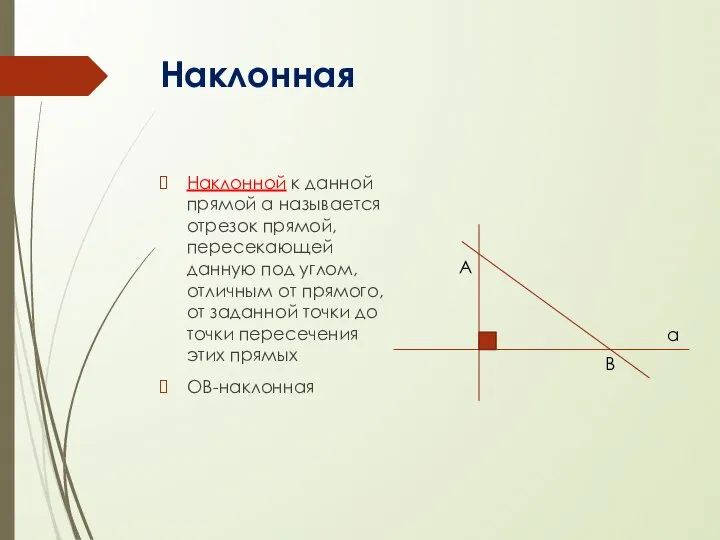
Наклонная
Наклонной к данной прямой а называется отрезок прямой, пересекающей данную под углом, отличным от прямого, от заданной точки до точки пересечения этих прямых
ОВ-наклонная
А
В
а

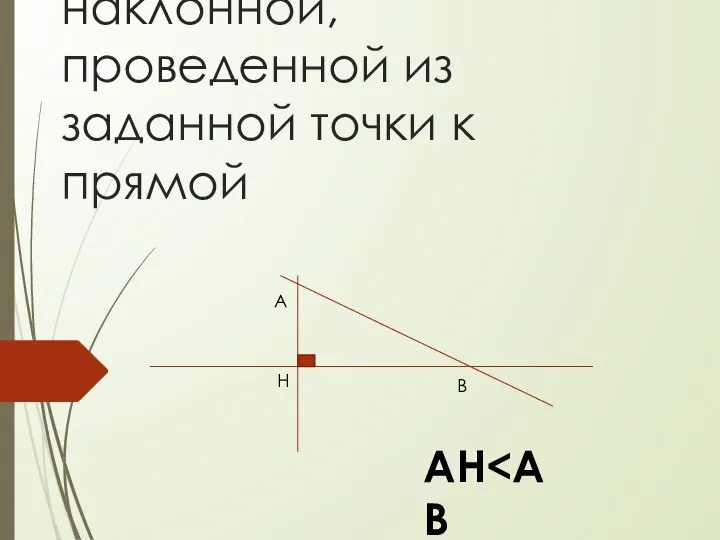
Перпендикуляр короче наклонной, проведенной из заданной точки к прямой
А
В
Н
АН<АВ

Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Доказательство:
Пусть точка А - точка, не лежащая на прямой ВС. Докажем сначала, что из точки А можно провести прерпендикуляр к прямой ВС.
Требуется доказать: что углы АВС и МВС равны