Содержание
- 2. Содержание Перпендикулярные прямые в пространстве Лемма Определение прямой, перпендикулярной к плоскости Теорема о перпендикулярности двух параллельных
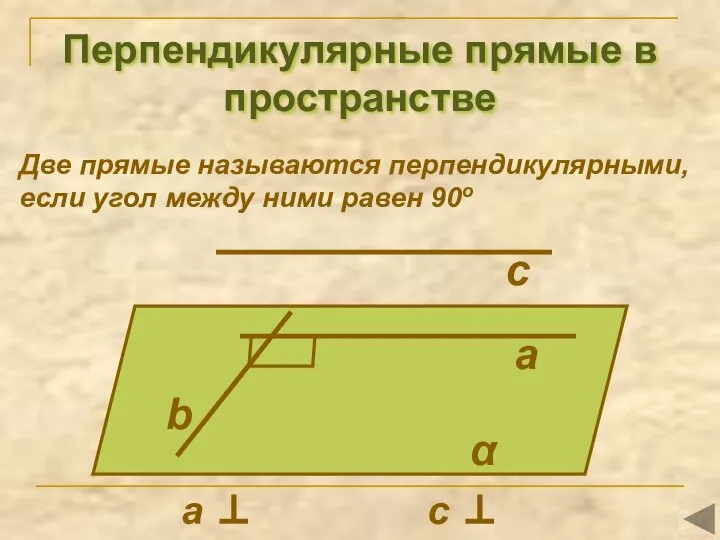
- 3. Перпендикулярные прямые в пространстве Две прямые называются перпендикулярными, если угол между ними равен 90о а b
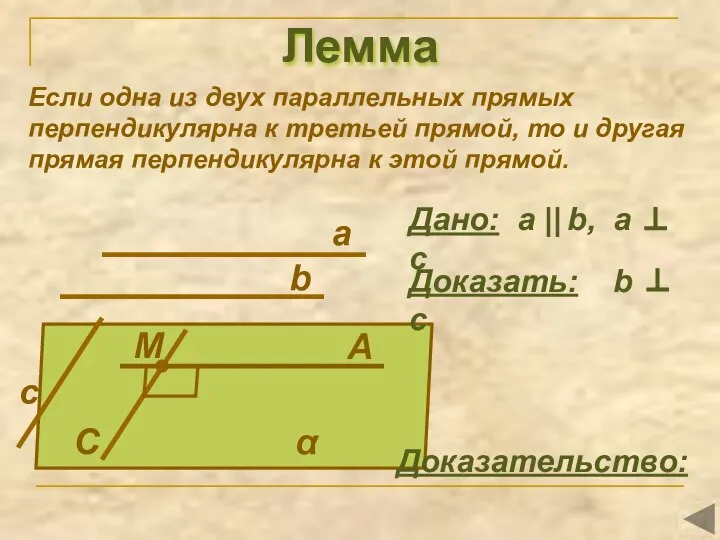
- 4. Лемма Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна
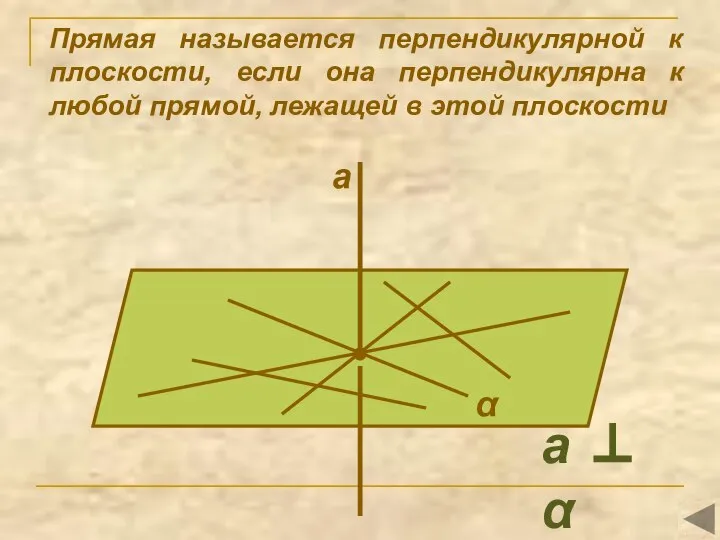
- 5. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости α
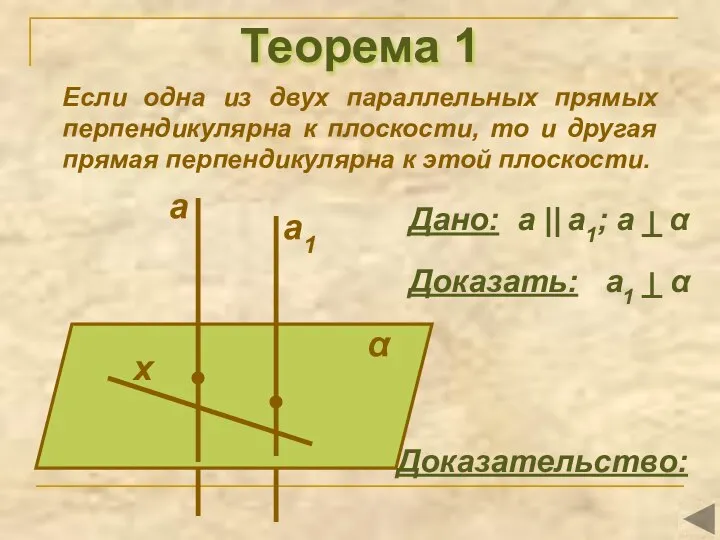
- 6. Теорема 1 Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна
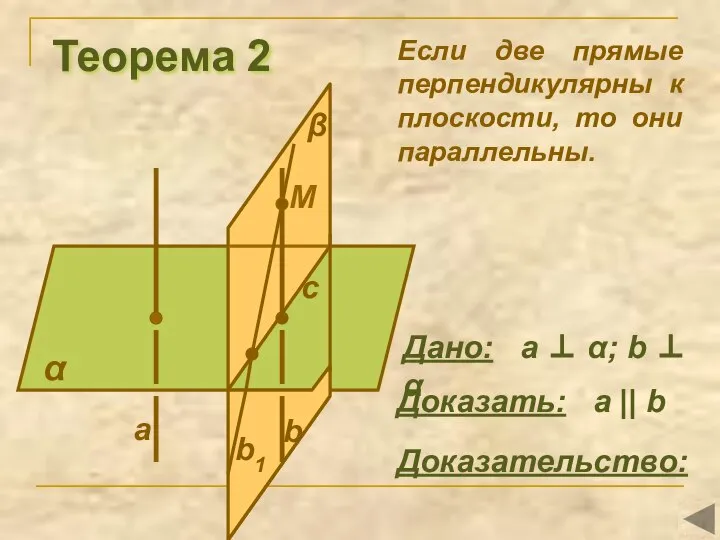
- 7. Теорема 2 α Доказать: а || b Доказательство: Если две прямые перпендикулярны к плоскости, то они
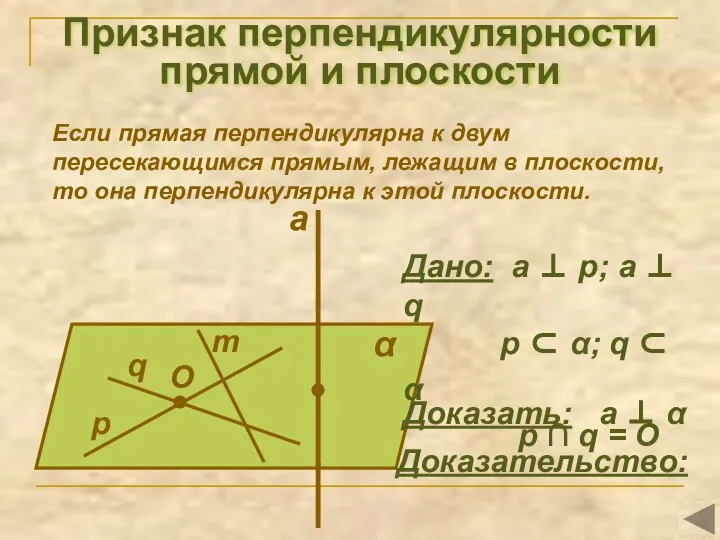
- 8. Признак перпендикулярности прямой и плоскости Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то
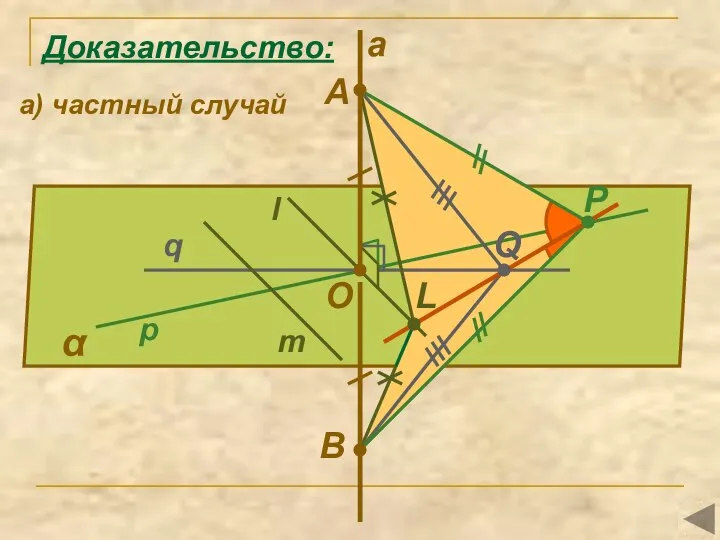
- 9. α q l m O a p B P Q Доказательство: L а) частный случай A
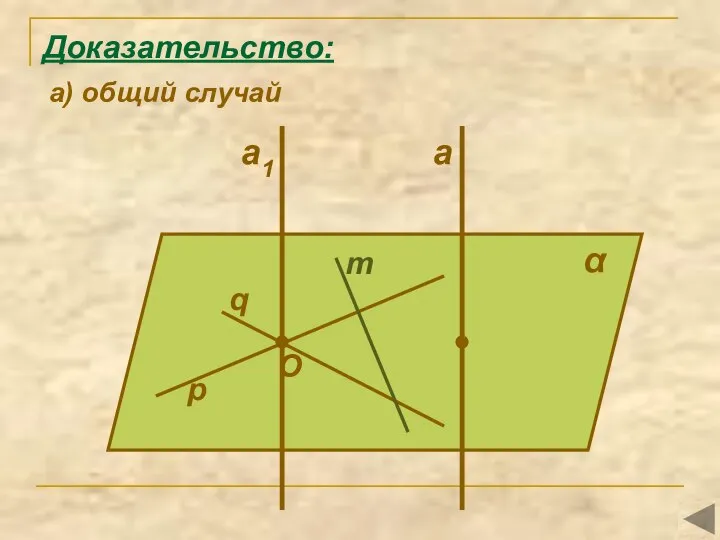
- 10. α q a p m O Доказательство: а) общий случай a1
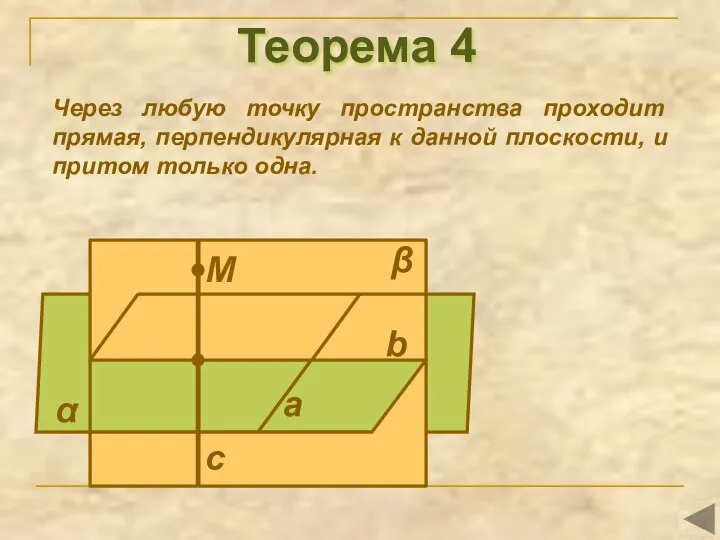
- 11. Теорема 4 Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
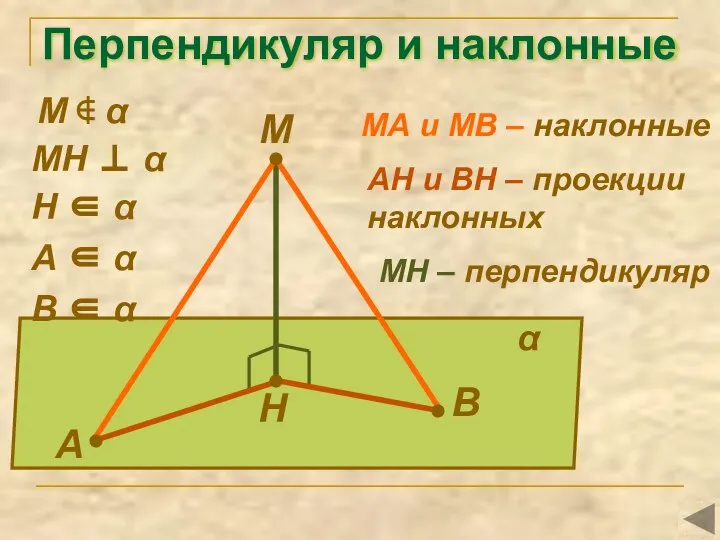
- 12. Перпендикуляр и наклонные М А В Н α МН ⊥ α А ∈ α В ∈
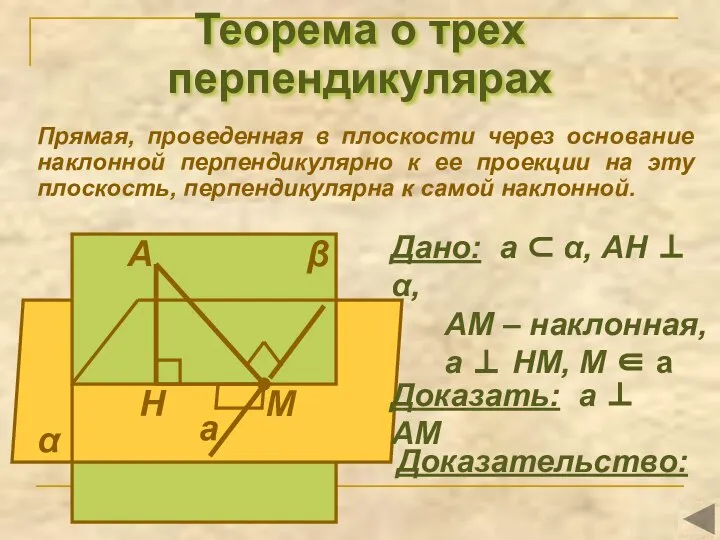
- 13. Теорема о трех перпендикулярах Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на
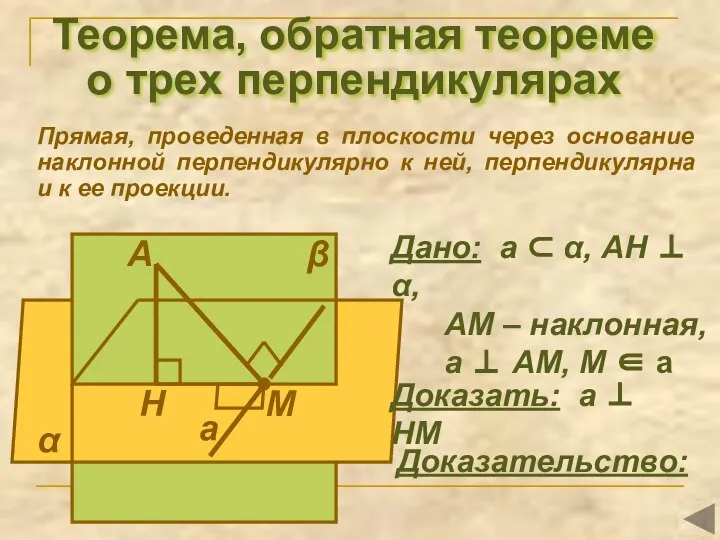
- 14. Теорема, обратная теореме о трех перпендикулярах Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней,
- 16. Скачать презентацию

 Дифференциальные уравнения и их применение в медицинской практике. Элементы комбинаторики. Случайные величины
Дифференциальные уравнения и их применение в медицинской практике. Элементы комбинаторики. Случайные величины Решение задач
Решение задач Окружность и круг
Окружность и круг Область определения функции
Область определения функции Проверочная работа на конец первой четверти в 5 классе
Проверочная работа на конец первой четверти в 5 классе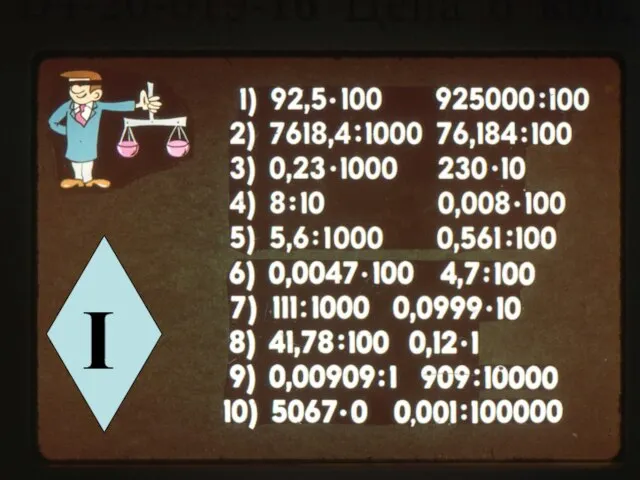 Округление десятичных дробей
Округление десятичных дробей Основные элементы комбинаторики и бином Ньютона. Решение задач. Тема 11.1
Основные элементы комбинаторики и бином Ньютона. Решение задач. Тема 11.1 Структура урока
Структура урока Тестирование
Тестирование Угол между векторами
Угол между векторами Презентация на тему Решение задач на пропорциональное деление (4 класс)
Презентация на тему Решение задач на пропорциональное деление (4 класс)  Логарифмы в профессиональной деятельности человека
Логарифмы в профессиональной деятельности человека Измерение ёмкости (вместимости). 3 класс
Измерение ёмкости (вместимости). 3 класс Занимательные головоломки
Занимательные головоломки Задачи на вычисление площади боковой поверхности циллиндра
Задачи на вычисление площади боковой поверхности циллиндра Математика в здоровье человека
Математика в здоровье человека Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Решение задач
Решение задач Арккосинус. Решение уравнения cos t = a
Арккосинус. Решение уравнения cos t = a قدرمطلقی درجه اول
قدرمطلقی درجه اول Лекция Алгебраические системы
Лекция Алгебраические системы Презентация на тему Сложение и вычитание натуральных чисел
Презентация на тему Сложение и вычитание натуральных чисел  Регрессионный анализ
Регрессионный анализ Скалярное произведение векторов
Скалярное произведение векторов Презентация на тему ВТОРОЙ И ТРЕТИЙ ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ
Презентация на тему ВТОРОЙ И ТРЕТИЙ ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ  Векторы. Понятие вектора
Векторы. Понятие вектора Евклидова геометрия
Евклидова геометрия Элементы теории графов
Элементы теории графов