Содержание
- 2. Например, имеются три участка земельной площади со сторонами квадрата: Х 1 – 100 м, Х 2
- 3. Средняя гармоническая Иногда при определении средних величин пользуются не их отдельными значениями, а обратными величинами. Обратные
- 5. Средняя гармоническая - величина обратная средней арифметической из обратных величин. ,тогда
- 6. фонд заработной платы Число рабочих = средняя месячная заработная плата Пример. = 36800
- 7. Средняя гармоническая взвешенная Средняя гармоническая взвешенная употребляется в тех случаях, когда необходимые веса (частоты) в исходных
- 8. Средняя геометрическая Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных
- 9. Пример. Имеются данные о прибыли предприятия за ряд лет: Найти средний годовой коэффициент роста прибыли. К1*К2*К3
- 11. Скачать презентацию








 Графики функций
Графики функций Подготовка к ВПР
Подготовка к ВПР Основные тригонометрические тождества. Преобразование тригонометрических выражений
Основные тригонометрические тождества. Преобразование тригонометрических выражений Aproximarea numerică a funcţiilor. Metode numerice – curs 11
Aproximarea numerică a funcţiilor. Metode numerice – curs 11 Признаки равенства треугольников
Признаки равенства треугольников Первообразная F'(x) = f(x)
Первообразная F'(x) = f(x) L_3_U
L_3_U Игра-тренажер Изучаем время
Игра-тренажер Изучаем время Презентация на тему Описательная статистика
Презентация на тему Описательная статистика  Презентация на тему Занимательная математика для детей (устный счёт + учимся писать цифры)
Презентация на тему Занимательная математика для детей (устный счёт + учимся писать цифры)  Сложение и вычитание чисел с разными знаками
Сложение и вычитание чисел с разными знаками Решение задач Параллельные прямые
Решение задач Параллельные прямые Задачи на построение
Задачи на построение Разложение на простые множители
Разложение на простые множители Исторические сведения
Исторические сведения Презентация на тему Сложение и вычитание именованных единиц
Презентация на тему Сложение и вычитание именованных единиц  Эталон и его назначение
Эталон и его назначение Решение логических задач
Решение логических задач Решение задач ( 8 класс)
Решение задач ( 8 класс) Тригонометрия. ЕГЭ, задание 7
Тригонометрия. ЕГЭ, задание 7 Семинар по математике
Семинар по математике Прямоугольник. Признак прямоугольника
Прямоугольник. Признак прямоугольника Измерение и построение углов
Измерение и построение углов График функции y = а(х – х0) +у0
График функции y = а(х – х0) +у0 Бинарный урок физики и геометрии
Бинарный урок физики и геометрии Презентация на тему Таблицы умножения и деления с числом 6
Презентация на тему Таблицы умножения и деления с числом 6  Проценты в медицине
Проценты в медицине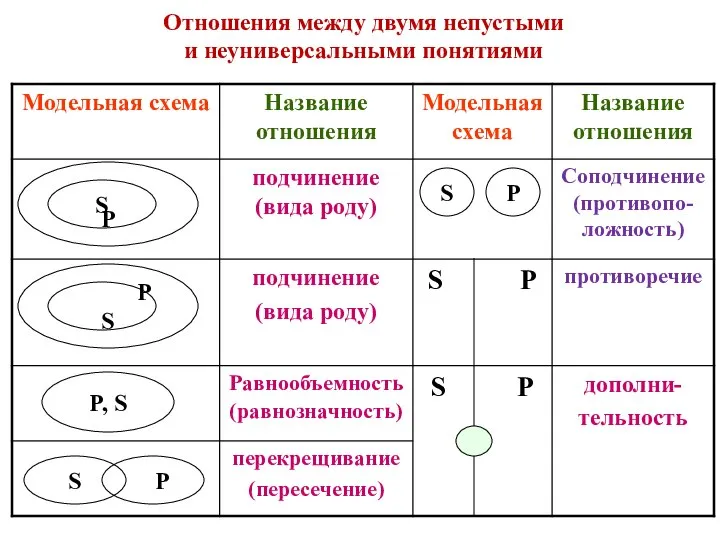 Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема
Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема