Статистический ряд

Порядок построения статистического ряда
1
2
Определить величину разряда по формуле
Определить границы каждого интервала (к Imin последовательно прибавлять ∆I).
Конец предыдущего интервала является началом последующего
3
4
5
Определяется частность попадания анализируемой величины в каждом разряде

2 Рассчитать вероятностные числовые характеристики
1
2
3
4

Порядок расчета вероятностных числовых характеристик наблюдаемой операции
1
2
3
Рассчитать для каждого интервала произведение частости попадания
на среднее значение интервала. Найти сумму полученных значений,
которая будет соответствовать математическому ожиданию
4
Рассчитать квадратическое отклонение
5
Определяется коэффициент вариации

3 Построить гистограмму и статистическую функцию распределения
Гистограмма
Графическое оформление статистического ряда
Для построения гистограммы на оси абсцисс откладываются интервалы размером ΔI, на этих интервалах как на основании строятся прямоугольники, площадь которых равна Рi, с высотой hi=Pi/ΔI
По средним значениям гистограммы строится кривая – которая называется статистической плотностью распределения
Необходимость построения
Для наглядного представления на какую теоретическую кривую похожа статистическая плотность распределения, чтобы ее использовать для сглаживания собранных данных и для дальнейших расчетов

Теоретические законы распределения случайных величин
Экспоненциальный закон
Наиболее часто используемые теоретические законы распределения непрерывной случайной величины
Делаем вывод, что по очертаниям полученная статистическая плотность распределения соответствует экспоненциальному закону
Необходимость сглаживания статистических данных с помощью теоретического закона
Нормальный закон
Где λ=1/М(I) – среднее количество операций, выполняемых за единицу времени
Теоретическая функция экспоненциального распределения - интеграл плотности распределения

4 Проверить гипотезу о соответствии выбранному теоретическому закону распределения случайной величины
1
2
3
Начальную оценку соответствия эмпирической функции распределения предполагаемому экспоненциальному закону распределения делаем путем визуального сравнения. На график наносим статистическую и теоретическую функцию
Вывод
экспоненциальное распределение не подходит для аппроксимации (выравнивания) распределения имеющихся статистических данных
Начальное предположение можно подтвердить посредством применения критерия согласия χ2 (критерий хи-квадрат), основанный на измерении отклонений между эмпирическими ni и теоретическими частотами oi, соответствующими различным интервалам построенной гистограммы
Теоретическая частота оi, - рассчитывается
При заданных ni и рассчитанных оi для каждого интервала i гистограммы мера отклонения между эмпирическими и теоретическими частотами определяется следующей формулой
Эмпирическая частота ni, - известна
Расчетная формула χ2
Расчетное значение χ2

4 Проверить гипотезу о соответствии выбранному теоретическому закону распределения случайной величины (продолжение)
4
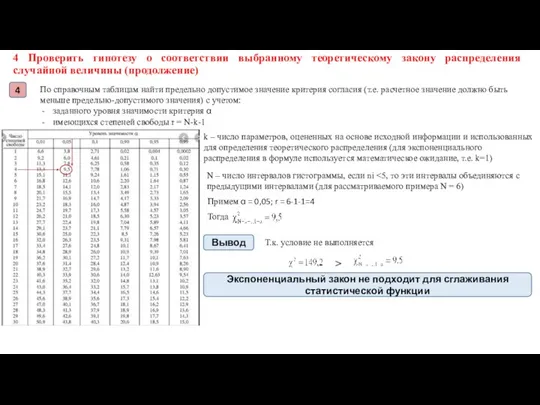
По справочным таблицам найти предельно допустимое значение критерия согласия (т.е. расчетное значение должно быть меньше предельно-допустимого значения) с учетом:
заданного уровня значимости критерия α
имеющихся степеней свободы r = N-k-1
Вывод
Экспоненциальный закон не подходит для сглаживания статистической функции
N – число интервалов гистограммы, если ni <5, то эти интервалы объединяются с предыдущими интервалами (для рассматриваемого примера N = 6)
Примем α = 0,05; r = 6-1-1=4
k – число параметров, оцененных на основе исходной информации и использованных для определения теоретического распределения (для экспоненциального распределения в формуле используется математическое ожидание, т.е. k=1)
Тогда
Т.к. условие не выполняется
>

5 Построить СМО железнодорожной станции
СМО (Система массового обслуживания) – один из методов математического моделирования
Цель моделирования
установление реальных простоев вагонов на станции с учетом неравномерности технологических операций, приводящих к колебанию продолжительности их выполнения и возникновению простоев в ожидании этих операций.
Основной принцип
Станцию представляют в виде совокупности подсистем с учетом фазового или линейного их взаимодействия между собой. Каждый элемент модели соответствует технологической операции, выполняемой каналом обслуживания.
Наличие элементов определяется наличием парков на станции
Объемы работы определяются размером движения и количеством подач на грузовые фронты
Таблица 4 – Поездопотоки, поступающие на станцию
Таблица 3 – Наличие парков на станции (1 вариант)
Таблица 3 – Наличие парков на станции (2 вариант)

6 Рассчитать расчетные характеристики для заданных технологических операций
Есть статистика выполнения исследуемой операции
Математическое ожидание продолжительности выполнения операций (основная расчетная характеристика) устанавливается с использованием метода обработки статистических данных
Нет статистики выполнения исследуемой операции
Корректировка технологических нормативов выполняется по формуле (1) для маневровых операций (за исключением интервала роспуска состава на горке) и (2) для остальных станционных технологических операций
Коэффициенты вариации продолжительности операций принимаются на основании среднесетевых значений, представленных в таблице.
Таблица - Приблизительные значения коэффициентов вариации

7 Рассчитать загрузку каналов элементов СМО
Если канал, обслуживающий систему, выполняет только одну операцию
загрузка системы
ρ=λ /μ
λ – интенсивность поступления поездов в каждую из систем (соответствует числу обрабатываемых составов/передач за сутки)
μ - интенсивность выхода поездов из рассматриваемой системы
К – количество каналов
Если канал, обслуживающий систему, обслуживает и другие системы
Если канал обслуживает несколько систем, необходимо определить суммарную загрузку канала путем сложения всех временных затрат на выполнение операций рассматриваемым каналом, чтобы установить не превышение допустимых значений (0,9)
Если при расчете ρканал>1, то необходимо рассмотреть меры по сокращению загрузки