Содержание
- 2. Сочетания и фигурные числа Задача 1. Путник хочет попасть из пункта А в пункт В кратчайшим
- 3. фигурные числа Сопоставим каждому пути из А в В последовательность из нулей и единиц – если
- 4. Арифметический квадрат
- 5. фигурные числа Дело в том, что числа 1, 2, 3, … можно изображать строками из одной,
- 6. фигурные числа Треугольники, изображенные на рис 4., можно объединять в пирамиды (рис. 7). Число точек в
- 7. Неравенство Бернулли c > 1 + n (c – 1), где с – произвольное число, большее
- 8. Неравенство Бернулли Неравенство Бернулли утверждает, что если х>-1, то для всех натуральных значений n выполняется неравенство
- 9. Пример 1. Доказать, что для любых n ϵ N Доказательство. Положив х=0,5 и применив теорему Бернулли
- 10. Задача 1. Из данной пропорции найти x и y. Решение. Записав отдельно отношение первого члена пропорции
- 11. Задача 2
- 13. Задача Доказать, что делится нацело на 64 при любом натуральном n. Доказательство. Обозначив выражение в скобках
- 14. Принцип Дирихле
- 15. Принцип Дирихле Если k+1 или более объектов расположены в k коробках, тогда есть по крайней мере
- 16. Реализация принципа Дирихле Если n объектов расположены в k коробках, то как минимум одна коробка содержит
- 17. Принцип Дирихле Пример Сколько человек из 100 родились в одном месяце? Среди 100 человек есть по
- 18. Раскладки В задачах на раскладки элементы раскладываются в несколько «ящиков» и надо найти число способов это
- 19. Раскладки Задача 1. Шары и лузы. Скольким способами могут распределиться 15 перенумерованных бильярдных шаров в 6
- 20. Вторая строка этой схемы не что иное, как бланк длины 15, заполненный цифрами 1, 2, 3,
- 21. Раскладки Вывод: Число способов размещения n различных предметов по m различным «ящикам» равно
- 22. Раскладки Задача 2. Сбор яблок. Трое ребят собрали с яблони 40 яблок. Сколькими способами они могут
- 23. Раскладки Мы имеем дело с сочетаниями с повторениями - есть 3 типа предметов (мальчики) и надо
- 24. Раскладки Вывод: Число способов размещения n одинаковых предметов по m различным ящикам равно
- 25. Раскладки Задача 3. Тайным голосованием 30 человек голосуют по 5 предложениям. Сколькими способами могут распределиться голоса,
- 26. Раскладки Ответ: Так как не учитывается порядок голосов, а учитывается только их количество, то надо распределить
- 27. Раскладки Задача 4. Сколькими способами можно расположить в 9 лузах 7 белых шаров и 2 черных
- 28. Раскладки 7 белых шаров можно разместить в 9 лузах способами 2 черных шара способами. Всего имеем
- 29. Раскладки
- 30. Раскладки Задача 5. Двое ребят собрали 10 ромашек, 15 васильков и 14 незабудок. Сколькими способами они
- 31. Раскладки Решение: Так как цветы каждого вида можно делить независимо от цветов другого вида, то по
- 32. Раскладки Задача 6. Сколькими способами можно разделить 10 белых грибов, 15 подберезовиков и 8 подосиновиков между
- 33. Раскладки
- 34. Подобная формула верна и в общем случае. Если имеется n1 предметов одного вида, n2 предметов другого
- 35. Разбиения и полиномиальная теорема Разбиением множества A на k частей называется семейство его подмножеств, такое, что
- 36. Если порядок частей существенен (т.е. разбиения, отличающиеся одно от другого только перестановкой частей, считаются различными), то
- 37. Задача. Сколькими способами можно расставить белые фигуры (короля, ферзя, две ладьи, двух слонов и двух коней)
- 38. Величина обозначается Через или и называется полиномиальным коэффициентом.
- 39. Полиномиальная формула: Где сумма распространена на всевозможные разбиения n1+n2+…+nk числа n на k целых неотрицательных слагаемых.
- 40. Получим всевозможные перестановки с повторениями, составленные из букв х1, х2,..., хk такие, что в каждую перестановку
- 41. Пример 1 Написать разложение полинома третьей степени Задание: определить полиномиальные коэффициенты в данном разложении
- 42. Пример 2 Найти разложение степени тринома
- 43. Пример. Найти коэффициент при из разложения степени Коэффициент при из разложения степени равен Имеем член разложения
- 44. Пример.
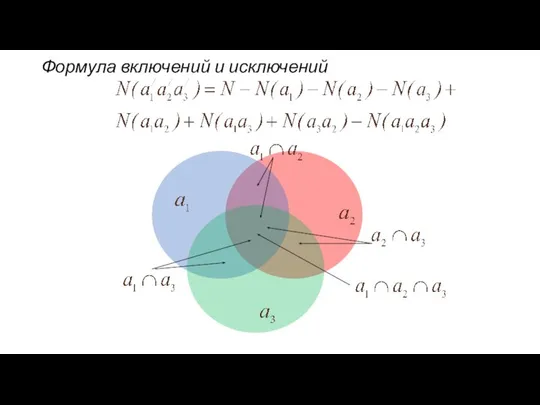
- 46. Формула включений и исключений
- 47. Формула включений и исключений Пусть даны N объектов (предметов), каждый из которых может обладать или не
- 48. Формула включений и исключений Если все свойства ai попарно не совместимы (т.е. N(aiak)=0 при i ≠k),
- 49. Формула включений и исключений Тогда, очевидно, т.к. при вычитании N(а1) и N(a2) из общего числа предметов
- 50. Формула включений и исключений
- 51. Формула включений и исключений При произвольном n справедлива формула включений и исключений:
- 52. Формула включений и исключений Сколько положительных целых чисел, не превышающих 1000, делятся на 7 или на
- 53. Пример.
- 54. 11 22 33
- 55. Рекуррентные соотношения
- 56. Рекуррентные соотношения При решении многих комбинаторных задач используется метод сведения данной задачи к аналогичной задаче, касающейся
- 57. Примеры рекуррентных формул
- 58. Линейные рекуррентные соотношения Рекуррентное соотношение вида an=b1(n)an-1+b2(n)an-2+b3(n)an-3+…+bp(n)ap называется линейным рекуррентным соотношением порядка р , т.к. аn
- 59. Рекуррентные соотношения Примеры 1) 2) 3) an+2=an·an+1-3an+1+1 - нелинейное рекуррентное соотношение порядка 2, т.к. зависит от
- 60. Линейные рекуррентные соотношения Решением рекуррентного соотношения является последовательность, при подстановке которой соотношение тождественно выполняется. Решение рекуррентного
- 61. Линейные рекуррентные соотношения с постоянными коэффициентами Линейное рекуррентное соотношение вида an=b1an-1+b2an-2+b3an-3+…+bpaр, bp≠0 c постоянными коэффициентами bi
- 62. Числа Фибоначчи
- 63. Последовательность (числа) Фибоначчи Числовая последовательность, в которой каждое число равно сумме двух предыдущих, называется последовательностью Фибоначчи
- 64. Числа Фибоначчи. Пример Пара кроликов приносит раз в месяц приплод из двух крольчат (самки и самца),
- 65. Числа Фибоначчи. Пример Fn – количество пар кроликов через n месяцев. Через n+1 месяцев будет Fn
- 66. Отношения вида an+2=b1an+1+b2an Решение данных отношений основано на следующих утверждениях: 1) a1(n) и a2(n) – решения
- 67. Решение отношений вида an+2=b1an+1+b2an 1) Составляем квадратное уравнение r2=b1r+b2, которое является характеристическим для данного отношения. 2)
- 68. Общее решение для рекуррентного отношения для чисел Фибоначчи Fn= Fn-1 +Fn-2 Характеристическое уравнение: r2=r+1 Корни уравнения:
- 69. Числа Фибоначчи для начальных условий F0=0, F1=1
- 71. Скачать презентацию



































































 Стохастические процессы
Стохастические процессы Презентация на тему Графическое решение уравнений
Презентация на тему Графическое решение уравнений  Старинные меры массы и длины
Старинные меры массы и длины Комплексные числа. Все формы
Комплексные числа. Все формы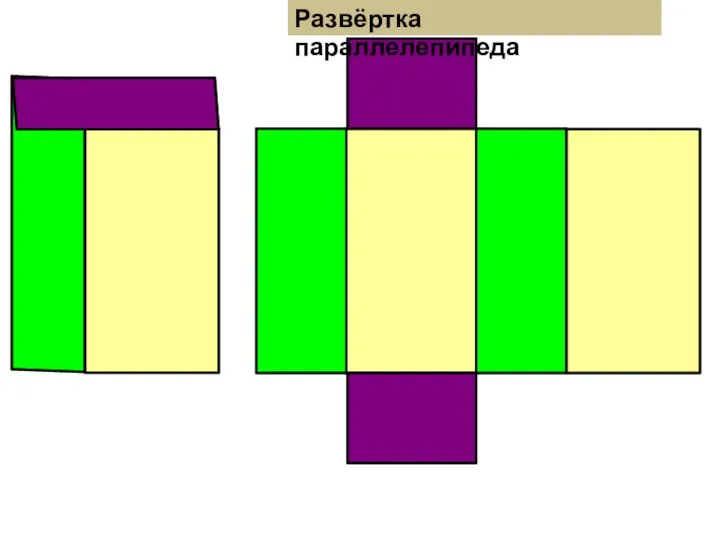 Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс
Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс Тригонометрические уравнения
Тригонометрические уравнения Квадратичная функция и её график. Методические материалы урока
Квадратичная функция и её график. Методические материалы урока Презентация на тему Объём многогранника
Презентация на тему Объём многогранника  Сближение меридианов. Международное геомагнитное аналитическое поле IGRF
Сближение меридианов. Международное геомагнитное аналитическое поле IGRF Задачи про форматы листов. Решение практико-ориентированных задач
Задачи про форматы листов. Решение практико-ориентированных задач Метод обратной матрицы решения систем линейных уравнений
Метод обратной матрицы решения систем линейных уравнений Методика работы с задачей на круговое движение
Методика работы с задачей на круговое движение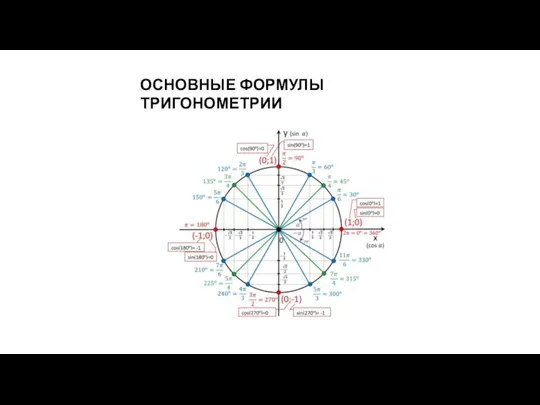 Основные формулы тригонометрии
Основные формулы тригонометрии Деление обыкновенных дробей
Деление обыкновенных дробей 7490_md_sin_cos_tg_0
7490_md_sin_cos_tg_0 Пирамида и её элементы. Правильная пирамида
Пирамида и её элементы. Правильная пирамида Математика вокруг нас
Математика вокруг нас Время. Единицы времени
Время. Единицы времени Первый замечательный предел
Первый замечательный предел Математика ЕГЭ. Углы и прямые
Математика ЕГЭ. Углы и прямые Линейная функция и её график
Линейная функция и её график Теория вероятностей в задачах ЕГЭ
Теория вероятностей в задачах ЕГЭ Основы логистики
Основы логистики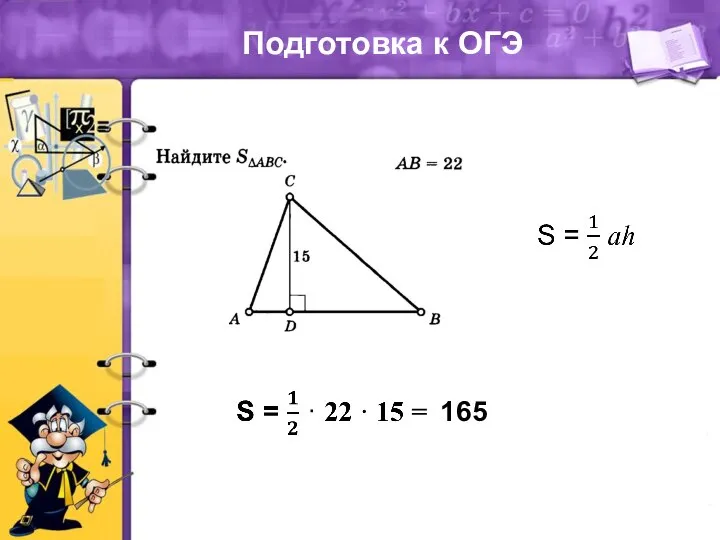 Теорема площади треугольника. Подготовка к ОГЭ
Теорема площади треугольника. Подготовка к ОГЭ Прямоугольник. Геометрия 8 класс
Прямоугольник. Геометрия 8 класс Логарифмические выражения
Логарифмические выражения Презентация по математике "Применение приёмов интерактивного обучения на уроках математики" -
Презентация по математике "Применение приёмов интерактивного обучения на уроках математики" -  Презентация на тему Метод координат в пространстве
Презентация на тему Метод координат в пространстве