Содержание
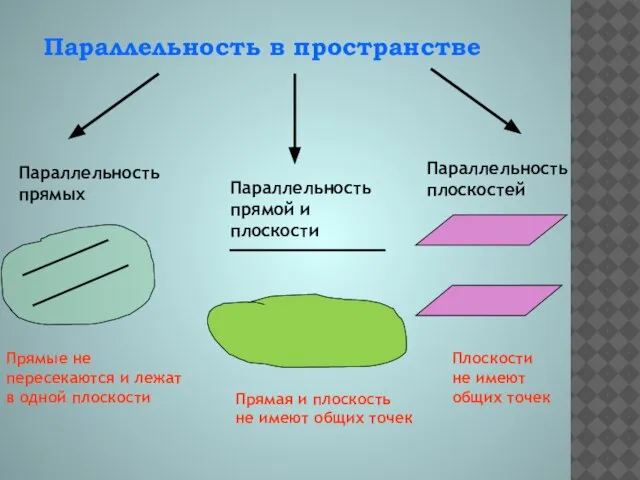
- 2. Параллельность в пространстве Параллельность прямых Параллельность прямой и плоскости Параллельность плоскостей
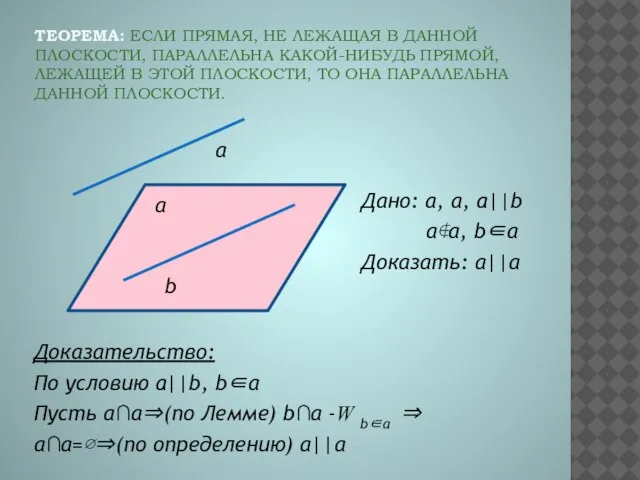
- 3. ТЕОРЕМА: ЕСЛИ ПРЯМАЯ, НЕ ЛЕЖАЩАЯ В ДАННОЙ ПЛОСКОСТИ, ПАРАЛЛЕЛЬНА КАКОЙ-НИБУДЬ ПРЯМОЙ, ЛЕЖАЩЕЙ В ЭТОЙ ПЛОСКОСТИ, ТО
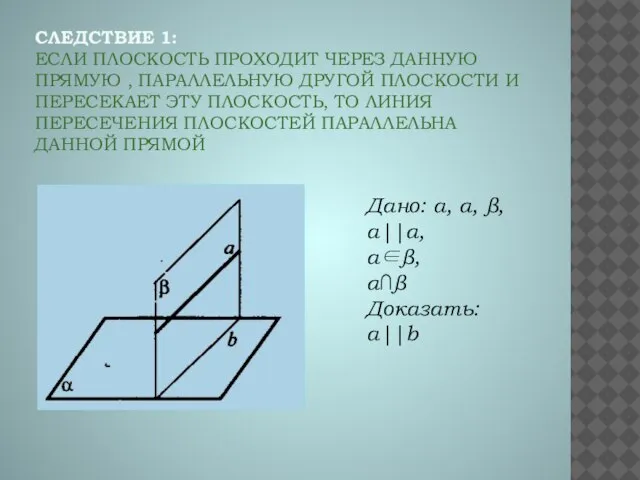
- 4. СЛЕДСТВИЕ 1: ЕСЛИ ПЛОСКОСТЬ ПРОХОДИТ ЧЕРЕЗ ДАННУЮ ПРЯМУЮ , ПАРАЛЛЕЛЬНУЮ ДРУГОЙ ПЛОСКОСТИ И ПЕРЕСЕКАЕТ ЭТУ ПЛОСКОСТЬ,
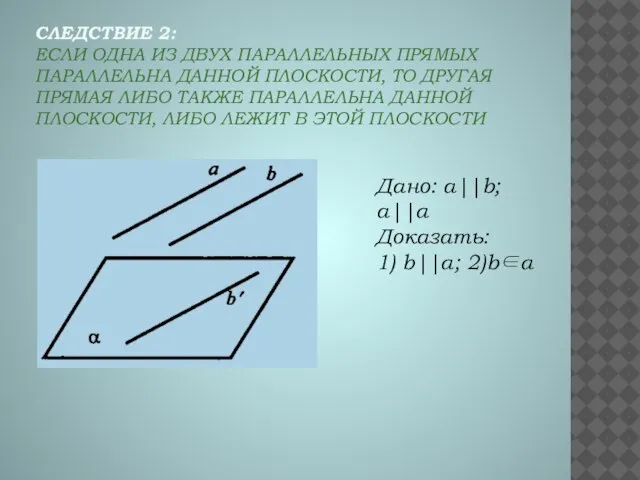
- 5. СЛЕДСТВИЕ 2: ЕСЛИ ОДНА ИЗ ДВУХ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ ПАРАЛЛЕЛЬНА ДАННОЙ ПЛОСКОСТИ, ТО ДРУГАЯ ПРЯМАЯ ЛИБО ТАКЖЕ
- 6. РЕШЕНИЕ ЗАДАЧ С КОММЕНТАРИЯМИ №18 (б) №20 №22 №26
- 8. Скачать презентацию

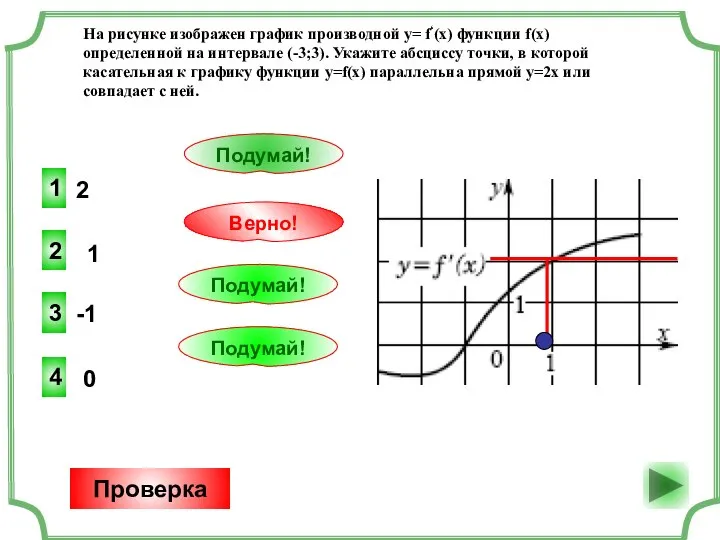 Решение задач
Решение задач Введение в стереометрию
Введение в стереометрию Вычисление предела
Вычисление предела калькуятор
калькуятор Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Презентация на тему Сложение и вычитание именованных единиц
Презентация на тему Сложение и вычитание именованных единиц  Презентация на тему Решение задач на нахождение неизвестного по двум разностям
Презентация на тему Решение задач на нахождение неизвестного по двум разностям  Решение задач с помощью уравнений
Решение задач с помощью уравнений Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной
Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной Первообразная и интеграл
Первообразная и интеграл ЭГЕ по математике. Прототип 18. Задачи с параметром. Применение свойств функции
ЭГЕ по математике. Прототип 18. Задачи с параметром. Применение свойств функции Прямоугольный треугольник. Решение задач по готовым чертежам
Прямоугольный треугольник. Решение задач по готовым чертежам Значения синуса, косинуса, тангенса для углов 30, 45, 60 градусов
Значения синуса, косинуса, тангенса для углов 30, 45, 60 градусов Прибавление +3. Вычитание -3
Прибавление +3. Вычитание -3 Теория оптимальной фильтрации и управления. Лекция № 7 (3/2)
Теория оптимальной фильтрации и управления. Лекция № 7 (3/2) Треугольники. Основные определения
Треугольники. Основные определения История введения понятия функции в школьный курс математики и современность
История введения понятия функции в школьный курс математики и современность Функции и графики. Элективный курс по математике. 9 класс
Функции и графики. Элективный курс по математике. 9 класс Прямоугольник. Геометрия 8 класс
Прямоугольник. Геометрия 8 класс Математические основы криптографии
Математические основы криптографии Неполные квадратные уравнения
Неполные квадратные уравнения Сумма углов треугольника. Решение задач
Сумма углов треугольника. Решение задач Среднее арифметическое. Задачи
Среднее арифметическое. Задачи Построение сечений в тетраэдре по трем точкам
Построение сечений в тетраэдре по трем точкам Решение заданий олимпиады по математике
Решение заданий олимпиады по математике Уравнения и неравенства с одной переменной
Уравнения и неравенства с одной переменной Урок математики. Таблица умножения на 7
Урок математики. Таблица умножения на 7 Классическое определение вероятности
Классическое определение вероятности