Слайд 2Пирамида
Пирамида - это многогранник,
основание которого - многоугольник,
а остальные грани

— треугольники,
имеющие общую вершину.
Слайд 3Многоугольник ABCD называется
основанием пирамиды,
треугольники ASD , DSC , CSB, BSA –

боковыми гранями пирамиды.
Точка S называется вершиной пирамиды,
а отрезки AS, DS, CS, BS - её
боковыми ребрами.
Слайд 4Перпендикуляр SO, проведенный
из вершины пирамиды
к плоскости основания,
называется высотой пирамиды

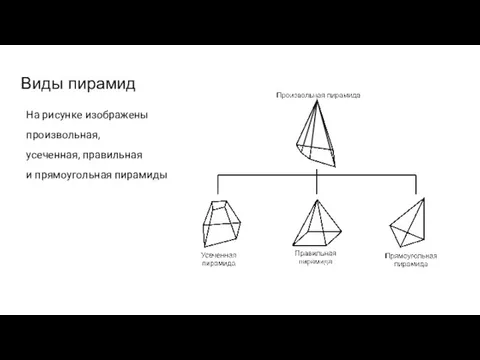
Слайд 5Виды пирамид
На рисунке изображены
произвольная,
усеченная, правильная
и прямоугольная пирамиды
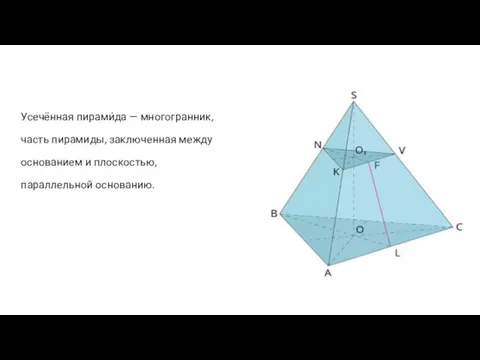
Слайд 6Усечённая пирами́да — многогранник,
часть пирамиды, заключенная между
основанием и плоскостью,
параллельной основанию.
Слайд 7Пирамида называется прямоугольной,
если одно из ее боковых ребер
перпендикулярно основанию
(оно же будет

и высотой).
Слайд 8Пирамида называется правильной,
если её основание –
правильный многоугольник,
а отрезок, соединяющий

вершину пирамиды
с центром основания, является её высотой.
Слайд 9Свойства боковых ребер и
боковых граней правильной пирамиды
Все боковые ребра правильной пирамиды

равны,
а боковые грани являются
равными равнобедренными треугольниками
Слайд 10
Высота боковой грани
правильной пирамиды,
проведенная из её вершины
называется апофемой.
Апофемы всех

боковых
граней равны.
Слайд 11Полная поверхность пирамиды
равна сумме боковой
поверхности пирамиды
и площади основания пирамиды
Боковая поверхность

пирамиды -
сумма площадей всех боковых граней.
Слайд 12Объем пирамиды
равен одной трети произведения
площади основания на высоту:
где S

– площадь основания,
H – высота пирамиды.












 Решение заданий ЕГЭ уровня С2 (1 часть)
Решение заданий ЕГЭ уровня С2 (1 часть) Сочетательное и распределительное свойство умножения. Урок 1
Сочетательное и распределительное свойство умножения. Урок 1 Признаки делимости на 2, 5,10, 3, 6 и 9
Признаки делимости на 2, 5,10, 3, 6 и 9 Параллельные прямые в пространстве
Параллельные прямые в пространстве Неопределенный интеграл
Неопределенный интеграл Урок 53. Расстояние от точки до прямой
Урок 53. Расстояние от точки до прямой Степень с рациональным показателем
Степень с рациональным показателем Косинус угла
Косинус угла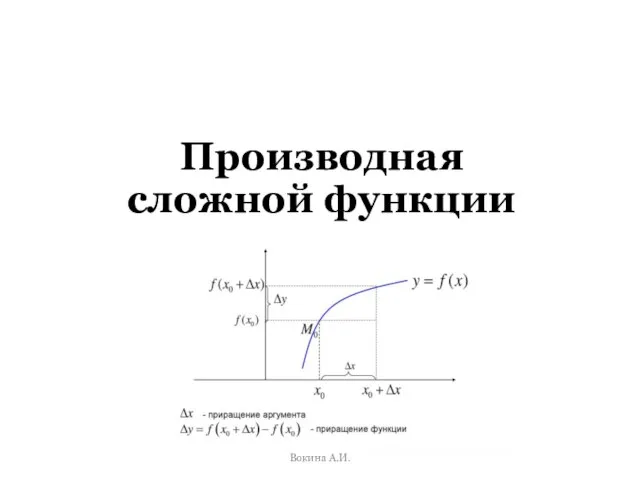 Производная сложной функции
Производная сложной функции Понятие вектора
Понятие вектора Определители. Матрица и ее определитель
Определители. Матрица и ее определитель Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Задания на развитие логики
Задания на развитие логики 20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами
20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами Деловая игра Маркетинг инноваций
Деловая игра Маркетинг инноваций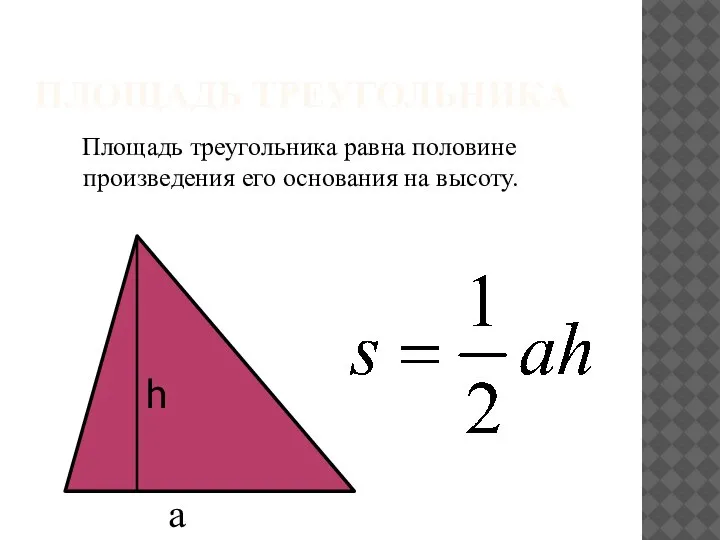 Площадь треугольника
Площадь треугольника Математика без границ. Конкурс
Математика без границ. Конкурс Сантиметр. Линейка
Сантиметр. Линейка Золотое сечение
Золотое сечение Информатика. Вероятность
Информатика. Вероятность Загадки и тайны треугольника
Загадки и тайны треугольника Сложение вида + 2, + 3
Сложение вида + 2, + 3 Презентация на тему Признаки равенства треугольников
Презентация на тему Признаки равенства треугольников  Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике)
Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике) Умножение одночлена на многочлен
Умножение одночлена на многочлен Современная финансовая математика
Современная финансовая математика Элементы круга и окружности в задачах ОГЭ
Элементы круга и окружности в задачах ОГЭ Плоскость и прямая в пространстве
Плоскость и прямая в пространстве