Содержание
- 2. Историчекая справка Термин «пирамида» заимствован из греческого «пирамис» или «пирамидос». Греки в свою очередь позаимствовали это
- 3. Гробницы фараонов (Египет)
- 4. Пирамиды в природе Гора Кайлас (Тибет)
- 5. Пирамиды в растениях
- 6. Пирамиды в архитектуре Стеклянная пирамида Лувра (Париж) Спасская башня Кремля (Москва)
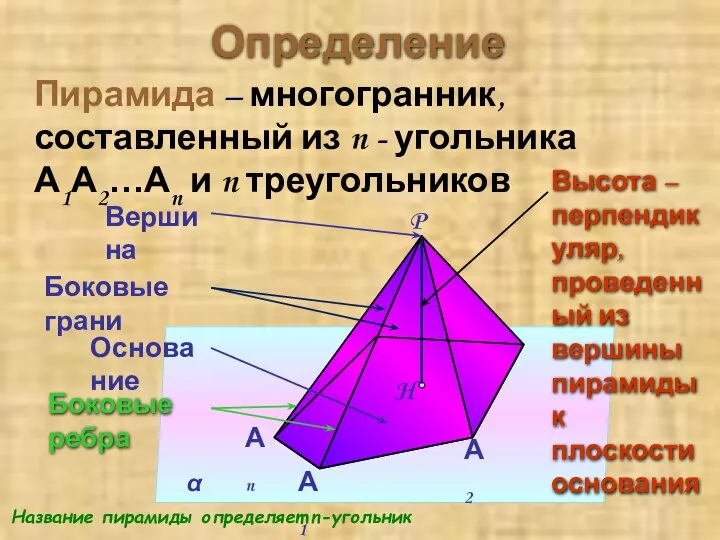
- 7. Определение Пирамида – многогранник, составленный из n - угольника А1А2…Аn и n треугольников Высота – перпендикуляр,
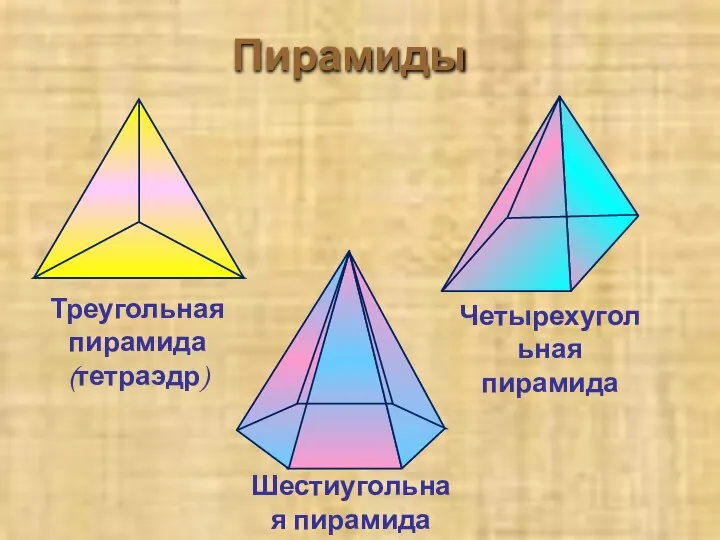
- 8. Пирамиды Треугольная пирамида (тетраэдр) Шестиугольная пирамида Четырехугольная пирамида
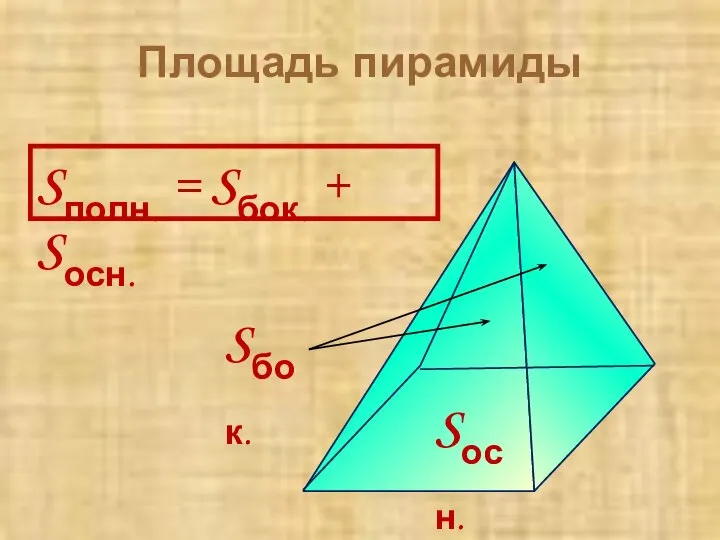
- 9. Площадь пирамиды Sполн. = Sбок. + Sосн. Sбок. Sосн.
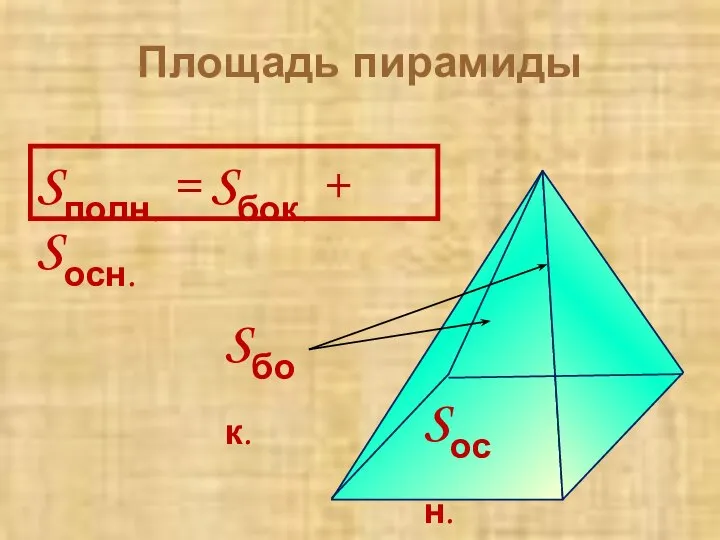
- 10. Площадь пирамиды Sполн. = Sбок. + Sосн. Sбок. Sосн.
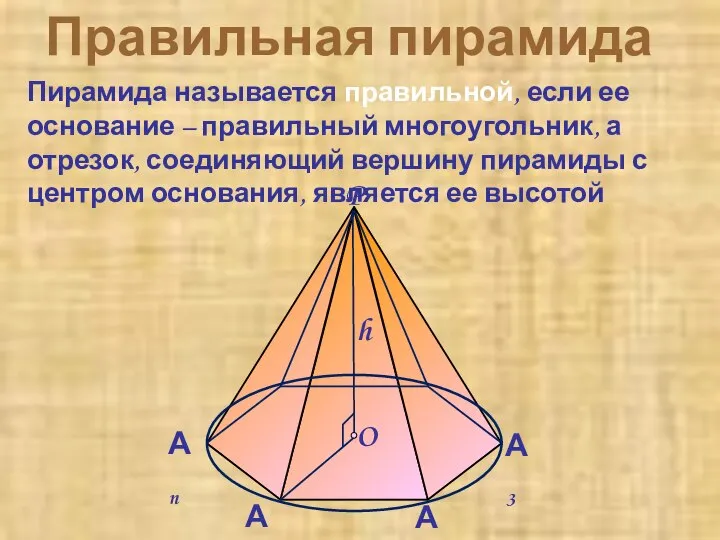
- 11. Правильная пирамида Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды
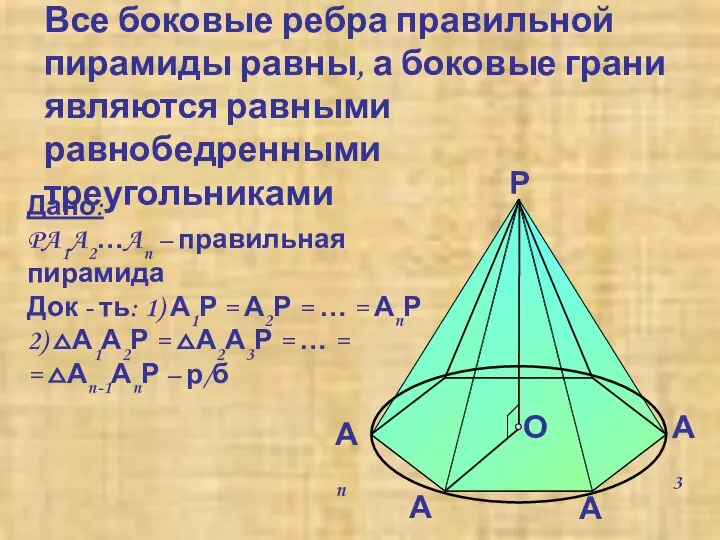
- 12. Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками Дано: PA1A2…An –
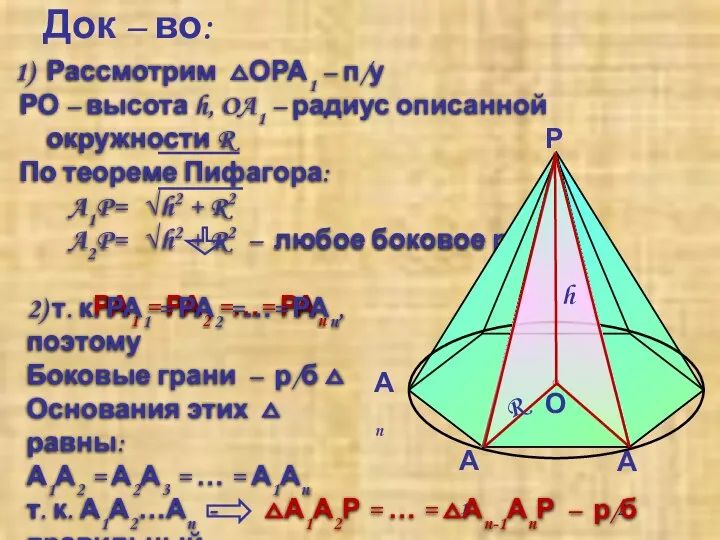
- 13. Док – во: 2) т. к. РА1 = РА2 =…= РАn, поэтому Боковые грани – р/б
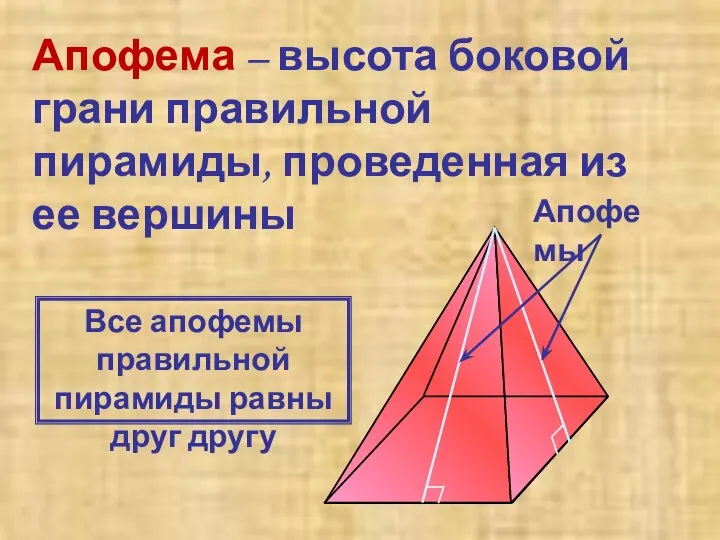
- 14. Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины Апофемы Все апофемы правильной пирамиды
- 16. Скачать презентацию





 Квадратный корень
Квадратный корень Планиметрия и стериометрия
Планиметрия и стериометрия Выражение длины вектора через его координаты
Выражение длины вектора через его координаты Различия между разными вариантами технологического процесса. Последовательный анализ
Различия между разными вариантами технологического процесса. Последовательный анализ Nepreryvnost_funktsii (1)
Nepreryvnost_funktsii (1) Уравнение и его корни
Уравнение и его корни Действия с алгебраическими дробями
Действия с алгебраическими дробями Метрология
Метрология Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена
Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена Алгоритм решения квадратного неравенства
Алгоритм решения квадратного неравенства Число 2. Цифра 2. Пара
Число 2. Цифра 2. Пара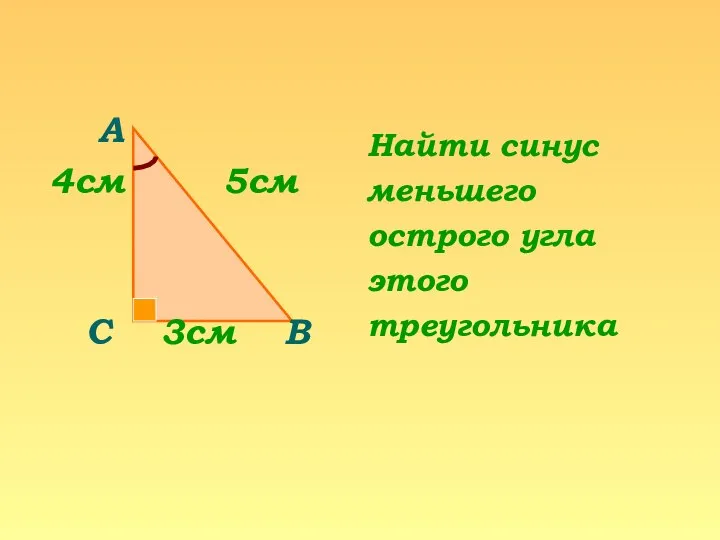 Устная работа на уроке геометрии
Устная работа на уроке геометрии Сечение тетраэдра
Сечение тетраэдра Поговорим о нуле
Поговорим о нуле Проценты
Проценты формулы нахождения периметра прямоугольника, периметра квадрата
формулы нахождения периметра прямоугольника, периметра квадрата Своя игра (4)
Своя игра (4) Определение понятия функция в толковых словарях
Определение понятия функция в толковых словарях Корень n-ой степени и его свойства
Корень n-ой степени и его свойства Презентация на тему Прямая пропорциональность
Презентация на тему Прямая пропорциональность  20f
20f Презентация на тему Решение систем линейных уравнений 7 класс для учителя
Презентация на тему Решение систем линейных уравнений 7 класс для учителя  Квадратные уравнения
Квадратные уравнения Сумма n первых членов геометрической прогрессии
Сумма n первых членов геометрической прогрессии Метод наименьших квадратов
Метод наименьших квадратов Умножение натуральных чисел. Графический диктант. 5 класс
Умножение натуральных чисел. Графический диктант. 5 класс Симплекс-метод. Тема 4
Симплекс-метод. Тема 4 Разложение суммы тригонометрических функций в произведение и наоборот
Разложение суммы тригонометрических функций в произведение и наоборот