Содержание
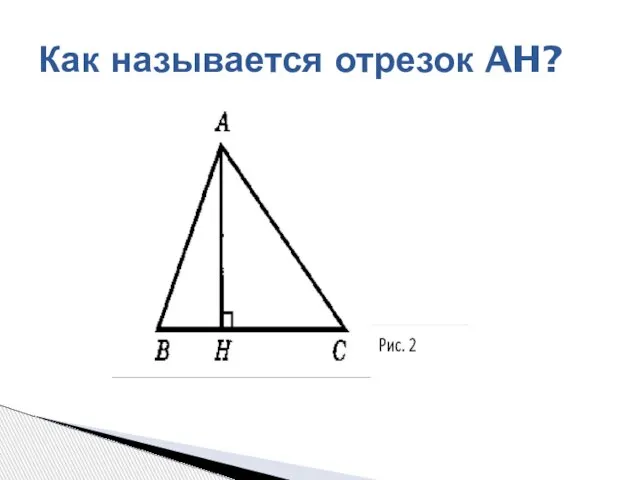
- 2. Как называется отрезок AH?
- 4. «Равнобедренный треугольник и его свойства» Тема урока:
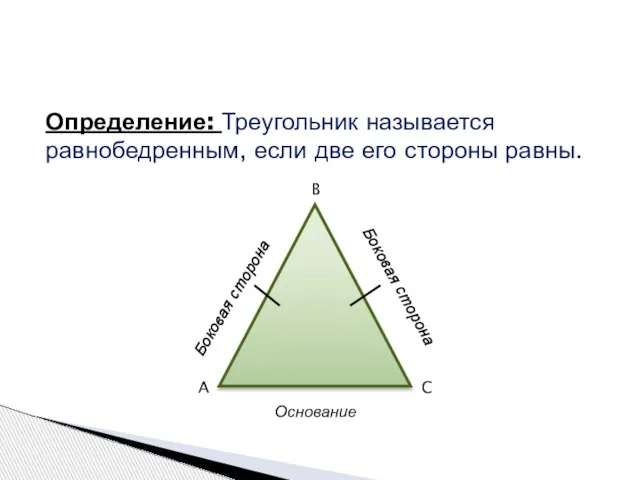
- 5. Определение: Треугольник называется равнобедренным, если две его стороны равны. A B C Боковая сторона Боковая сторона
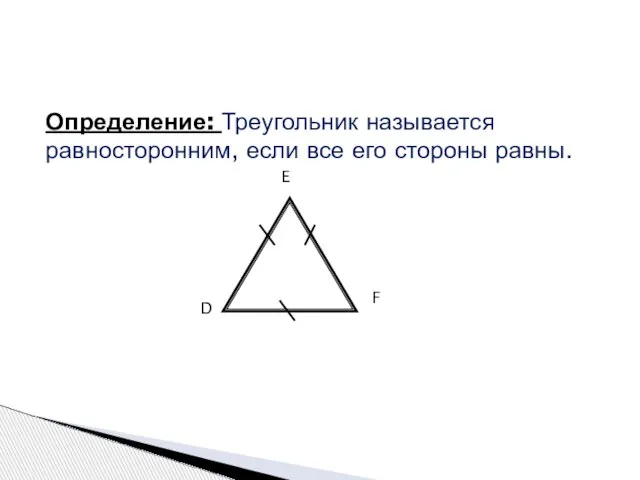
- 6. Определение: Треугольник называется равносторонним, если все его стороны равны. D E F
- 7. Свойства равнобедренного треугольника B A C
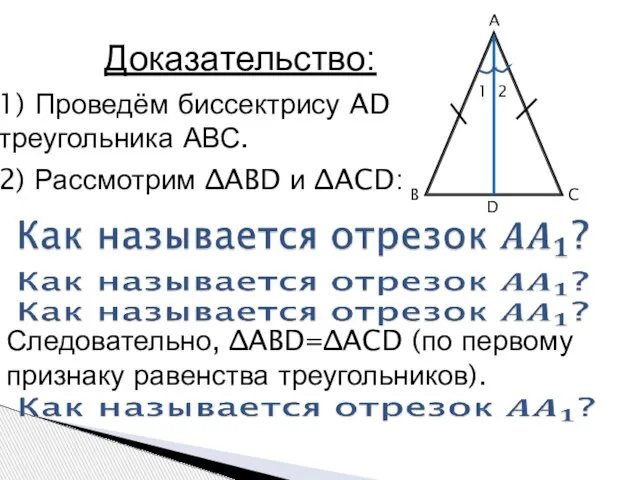
- 8. A B C D Доказательство: 1) Проведём биссектрису AD треугольника АВС. 2) Рассмотрим ∆ABD и ∆ACD:
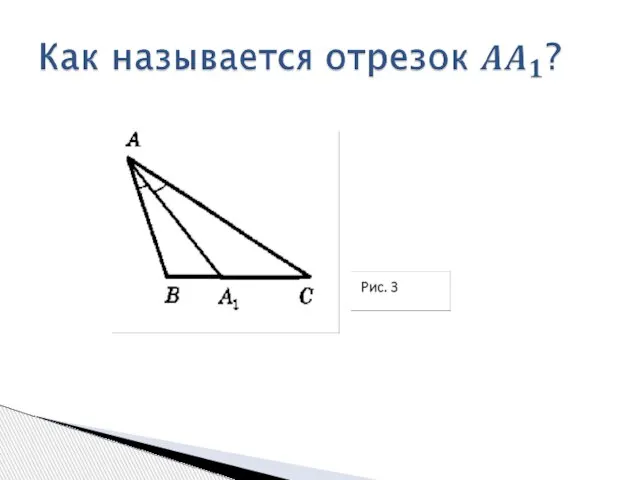
- 9. Теорема 2. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой. Дано: ∆ ABC
- 10. Доказательство: 1) Рассмотрим ∆ABD и ∆ACD: Следовательно, ∆ABD=∆ACD (по первому признаку равенства треугольников).
- 11. 1. Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой. 2. Медиана равнобедренного треугольника, проведённая
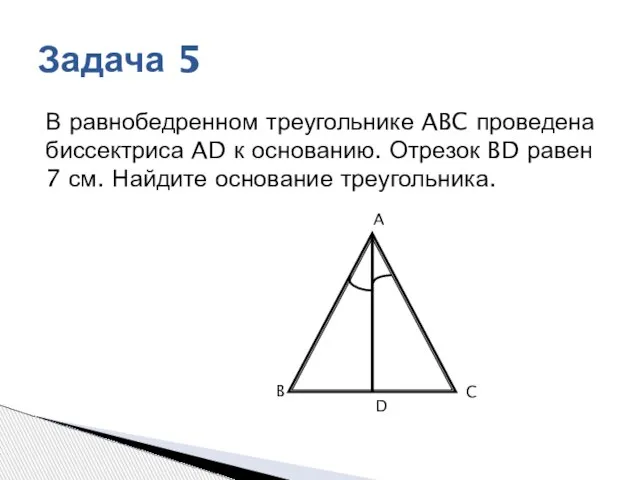
- 12. A B C Задача 4
- 13. В равнобедренном треугольнике ABC проведена биссектриса AD к основанию. Отрезок BD равен 7 см. Найдите основание
- 15. Скачать презентацию






 Случаи вычитания 11 -
Случаи вычитания 11 - Статистические графики
Статистические графики математика гр 32 парність-2.docx
математика гр 32 парність-2.docx Число та цифра 6
Число та цифра 6 Конус. Виды конусов. Конусы в нашей жизни
Конус. Виды конусов. Конусы в нашей жизни Сечения в многогранниках
Сечения в многогранниках Уравнение линии на плоскости. Уравнение фигуры. Уравнение окружности
Уравнение линии на плоскости. Уравнение фигуры. Уравнение окружности Решение задач с помощью уравнений
Решение задач с помощью уравнений Решение задач на движение
Решение задач на движение Понятие спирали
Понятие спирали Геометрические построения
Геометрические построения Элементы теории вероятностей
Элементы теории вероятностей Проценты
Проценты Математические ребусы
Математические ребусы Площади. ОГЭ
Площади. ОГЭ Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Текстовые задачи на движение по прямой
Текстовые задачи на движение по прямой Основное свойство дроби
Основное свойство дроби Две задачи на дроби
Две задачи на дроби Статистические гипотезы
Статистические гипотезы Собираем ягоды. Математика 1 класс. Итоговое повторение. Тренажёр
Собираем ягоды. Математика 1 класс. Итоговое повторение. Тренажёр Конструктивные объекты
Конструктивные объекты Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики?
Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики? Презентация по математике "Что такое понятие" -
Презентация по математике "Что такое понятие" -  Параллельность плоскостей
Параллельность плоскостей Экономический биатлон. “Экономика и математика”. Финал
Экономический биатлон. “Экономика и математика”. Финал Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними
Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними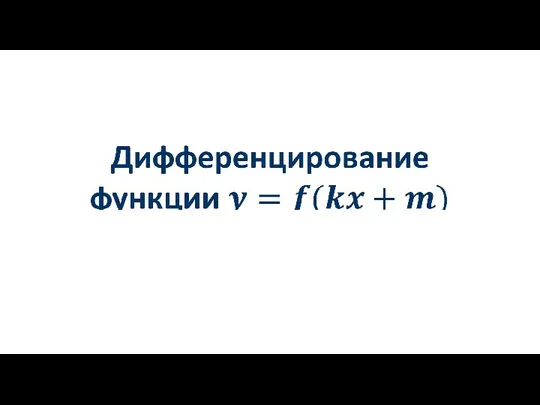 Дифференцирование функции y=f(kx+m)
Дифференцирование функции y=f(kx+m)