Способы извлечения квадратного корня из многозначных чисел

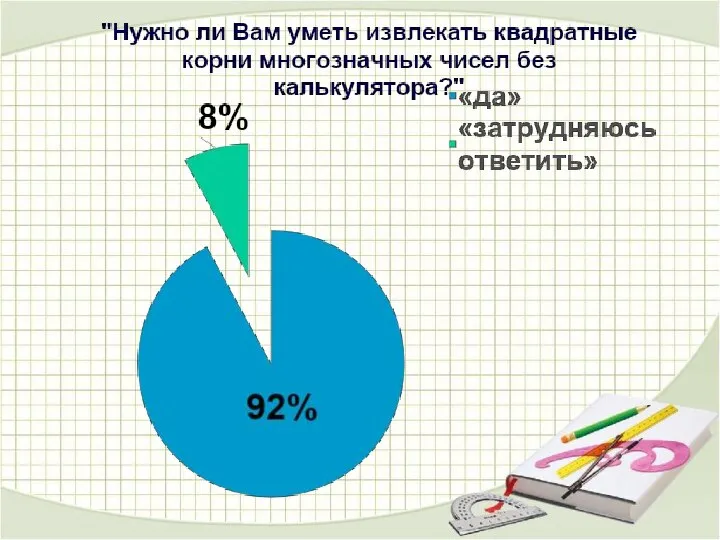
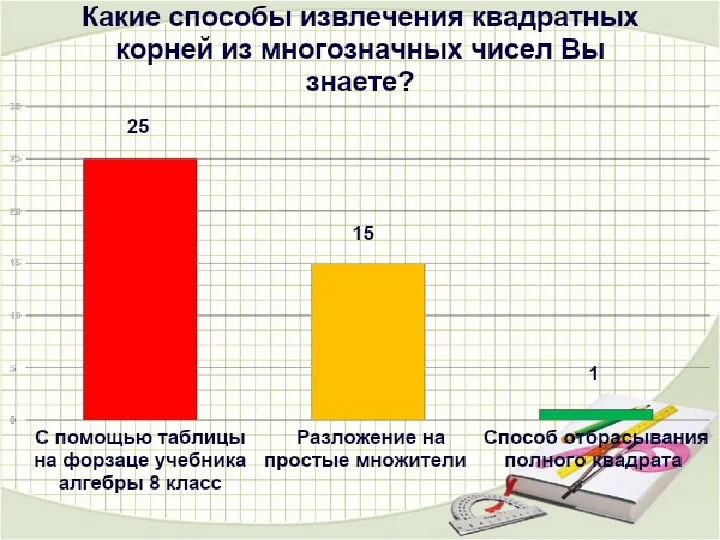
Вывод:
Результаты показали, что ученики хорошо
умеют пользоваться таблицей квадратов
двузначных чисел, но не умеют извлекать корни
из многозначных чисел больших 1002.

Цель работы:
изучить способы вычисления арифметических
корней и выбрать самый рациональный для
практического применения.

Задачи проекта:
1. Проанализировать путём соцопроса умение
учащихся извлекать квадратные корни без калькулятора;
2.Изучить математическую литературу по данной теме, используя Интернет-ресурсы;
3. Изучить способы и алгоритмы вычисления арифметического корня и рассмотреть примеры быстрого извлечения квадратного корня;
Классифицировать найденные способы извлечения корней по степени сложности, погрешности и практическому применению;
4. Познакомить одноклассников с самым
рациональным способом извлечения корней.

Актуальность
В школьном курсе математики часто встречаются задания с извлечением квадратного корня, в заданиях ОГЭ, в практических вычислениях и быту.
Умения извлекать квадратные корни нужны при изучении некоторых тем химии и физики .

Способ разложения на простые множители
Для извлечения квадратного корня можно разложить число на простые множители и извлечь квадратный корень из произведения.
1936 | 2 1521 | 3 968 | 2 507 | 3
482| 2 169 | 13
242| 2 13 | 13
121| 11 1 | 1
11| 11
1| 1
Не всегда легко можно разложить, занимает много времени.
√1936 = √24∙11² = 2∙2∙11 = 44
√1521 = √132 ∙ 32= 13∙3 = 39

Способ использования таблицы квадратов двузначных чисел
Закрыть две последние цифры, найти число, которое меньше подкоренного
73
=
?
7225
8
5
Используется только для корней до100, имеет точность только до десятых. Поможет на экзамене ученику.
8,5

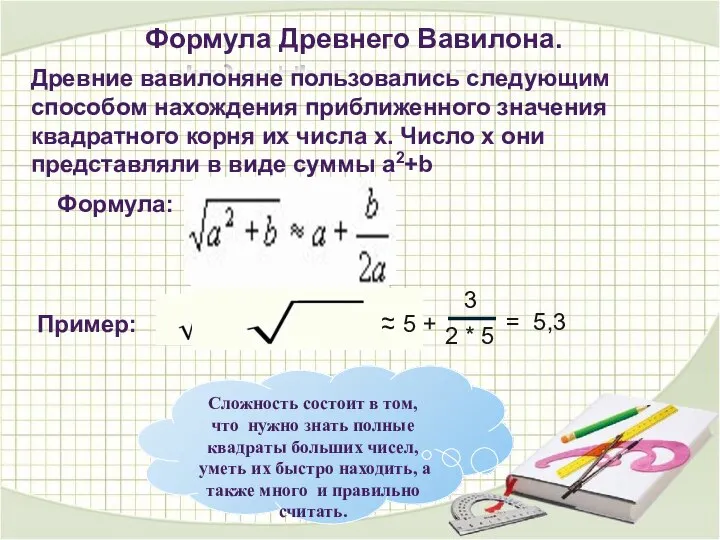
Формула Древнего Вавилона.
Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня их числа х. Число х они представляли в виде суммы а2+b
Формула:
Пример:
28
=
52+ 3
~
~
5 +
3
—
2 * 5
=
5,3
Сложность состоит в том, что нужно знать полные квадраты больших чисел, уметь их быстро находить, а также много и правильно считать.

Через решение уравнения
√121< √129 < √144
11 < √129 < 12
√129= 11 + х
(√129) ² = (11 + х)²
129 = (11 + х)² = 121 + 22х + х²
129 = 121 + 22х
х = 0,3636
Значит √ 129 ≈ 11 + 0,3636 ≈ 11,3636
√129 = ?
Такой способ интересный, но трудоёмкий. Больше применим к небольшим корням, где легко можно определить границы корня.

Способ отбрасывание полного квадрата
Выделяем из числа квадрат, который оканчивается той же цифрой, что и данное число
Извлечение корней до числа 752 =5625
2704
=
2700+4
=
27+25= 52
4624 = 4300+324= 43+25=68
Извлечение корней после 752 =5625
8836 =
8800+36=
88+6=
94
Этот способ плох, так как применим только для извлечения квадратного корня из точного квадрата, и имеет 2 алгоритма

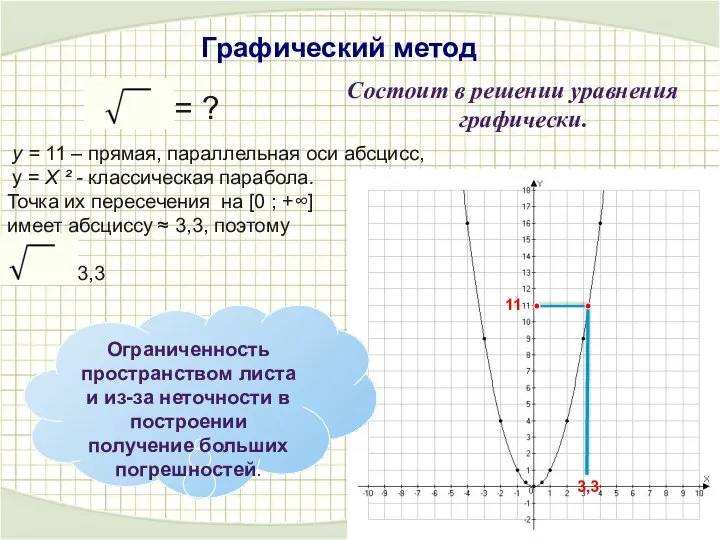
Графический метод
11 = ?
у = 11 – прямая, параллельная оси абсцисс,
у = Х ² - классическая парабола.
Точка их пересечения на [0 ; +∞]
имеет абсциссу ≈ 3,3, поэтому
11 ≈ 3,3
11
3,3
Состоит в решении уравнения графически.
Ограниченность пространством листа и из-за неточности в построении получение больших погрешностей.

Заключение
В ходе исследования, я убедился, что актуальность темы я выбрал правильную, ведь не только дети, но и взрослые не умеют вычислять квадратные корни без калькулятора, а это является важной составляющей в жизни людей. В результате проведённой работы, было найдено огромное количество способов вычисления квадратного корня, а также выявлено, что современной науке известно много таких способов, начиная со способа математиков Древнего Вавилона и заканчивая способом «Степенных рядов сложных степеней» из разделов высшей математики, но, к сожалению, не все они являются удобными и легкими в вычислениях. Методом проб и ошибок, я пришел к выводу, что самым рациональным и точным является способ «Решение уравнения». В ходе исследования были проработаны все способы, а их практическое применение доказало все недостатки и преимущества каждого из методов. Была дана характеристика каждого способа по таким критериям, как точность вычислений, трудоёмкость, «требует знания формул», «для каких корней применим», «требует логики или дополнительных знаний», а также насколько способ удобен, математически красив и практичен. В результате исследовательской работы я пришел к выводу, что извлечение квадратного корня без калькулятора является не только полезным занятием, но еще и очень увлекательным.