Содержание
- 2. Определение. Пусть каждому вещественному числу x из некоторого числового множества D поставлено в соответствие однозначно определенное
- 3. Множество D называется областью определения функции f, число x — ее аргументом, а число y —
- 4. Множество E = {y ∈ R: y = f (x), x∈D} называется областью значений функции f.
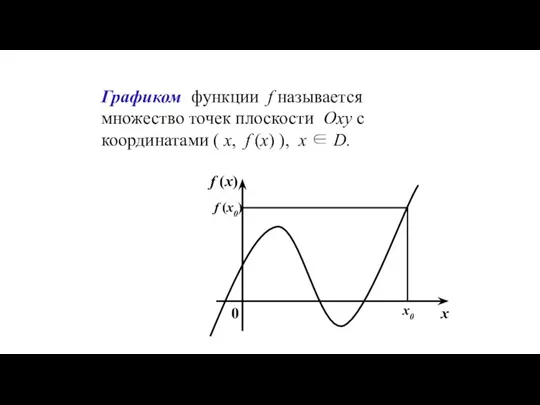
- 5. Графиком функции f называется множество точек плоскости Oxy с координатами ( x, f (x) ), x
- 6. Способы задания функций:
- 7. Способы задания функций: аналитический
- 8. Способы задания функций: аналитический: а) с помощью одной формулы, например, f (x) = 3x + 7;
- 12. Способы задания функций: графический;
- 13. Способы задания функций: графический; табличный, в виде
- 14. Способы задания функций: графический; табличный, в виде словесный – функция описывается правилом ее составления.
- 15. Основные свойства функций:
- 16. Основные свойства функций: Четность и нечетность Функция y = f(x) – четная, если для любого x
- 17. Основные свойства функций: Четность и нечетность Функция y = f(x) – нечетная, если для любого x
- 18. В противном случае, функция называется функцией общего вида. График четной функции симметричен относительно оси ординат, а
- 19. Основные свойства функций: Монотонность Функция f(x) называется возрастающей на промежутке [a; b], если для любых x1,
- 20. Основные свойства функций: Монотонность Функция f(x) называется убывающей на промежутке [a; b], если для любых x1,
- 21. Основные свойства функций: Монотонность Функции, возрастающие или убывающие называются монотонными.
- 22. Основные свойства функций: Ограниченность Функция f(x) называется ограниченной сверху на промежутке [a; b], если существует такое
- 23. Основные свойства функций: Ограниченность Функция f(x) называется ограниченной снизу на промежутке [a; b], если существует такое
- 24. Основные свойства функций: Ограниченность Функция, ограниченная на [a, b] и сверху, и снизу, называется ограниченной на
- 25. Основные свойства функций: Ограниченность Определение ограниченности функции может быть также записано в следующем виде: Функция называется
- 26. Основные свойства функций: Периодичность Функция y = f(x), называется периодичной с периодом T ≠ 0, если
- 27. Основные элементарные функции
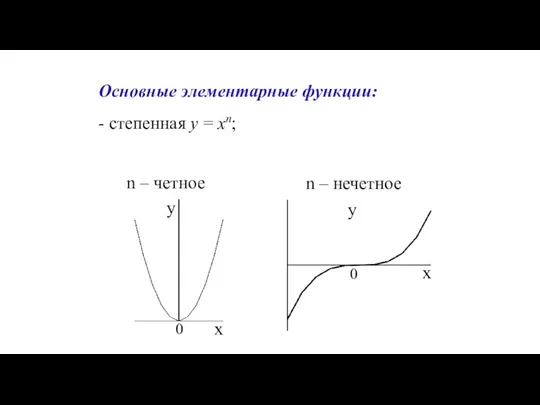
- 28. Основные элементарные функции: - степенная y = xn; n – четное n – нечетное
- 29. n – четное n – нечетное
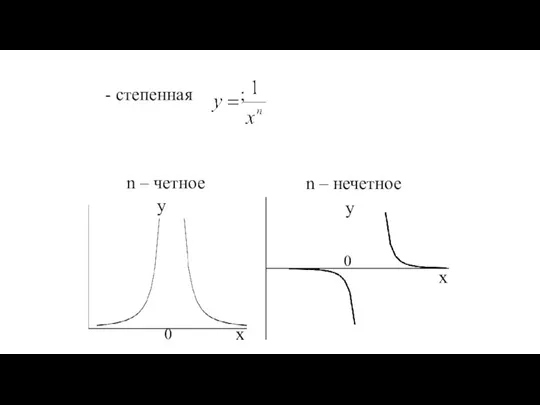
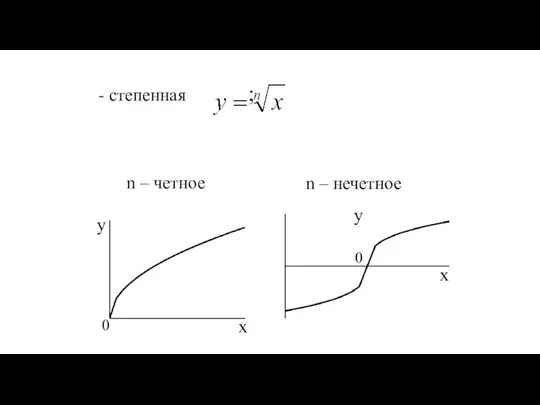
- 30. - степенная ; n – четное n – нечетное
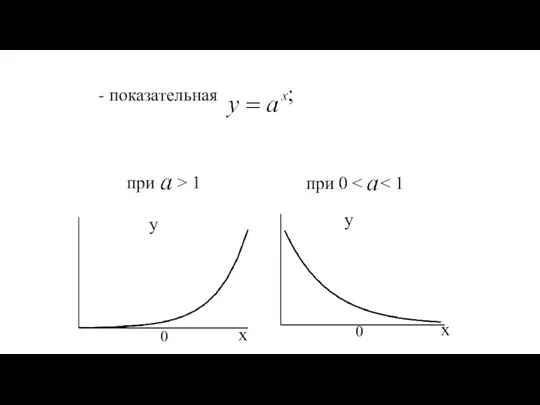
- 31. - показательная ; при > 1 при 0 y 0 x y 0 x
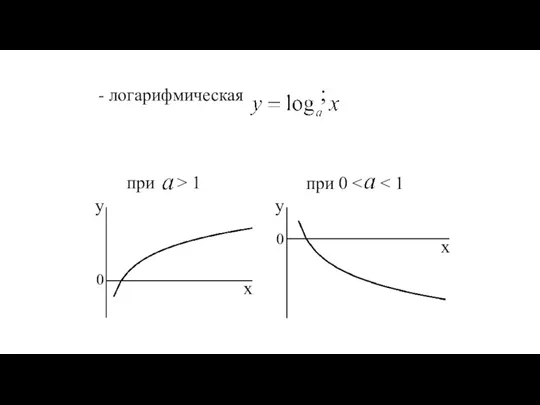
- 32. - логарифмическая ; при > 1 при 0 y 0 x y 0 x
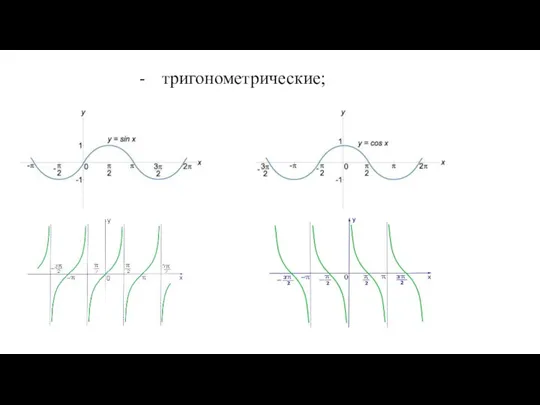
- 33. тригонометрические;
- 34. обратные тригонометрические функции.
- 35. Функции, полученные из основных элементарных функций с помощью арифметических действий и суперпозиции, называются элементарными.
- 36. §2. Последовательности
- 37. Определение. Если каждому числу n ϵ N поставлено в соответствие вещественное число хn, то образовавшееся таким
- 38. Числа хi называются элементами или членами последовательности, i – номер элемента, хn – общим членом последовательности.
- 39. Обычно числовая последовательность задаётся некоторой формулой общего члена хn = f(n), позволяющей найти любой член последовательности
- 40. Примеры числовых последовательностей 1, 2, 3, 4, 5, … – ряд натуральных чисел; 2, 4, 6,
- 41. Последовательность можно рассматривать как функцию с областью определения – множеством натуральных чисел. Следовательно, последовательность может обладать
- 42. Последовательность {хn} называют ограниченной сверху, если все ее члены не больше некоторого числа M.
- 43. Последовательность {хn} называют ограниченной сверху, если все ее члены не больше некоторого числа M. Пример: -1,
- 44. Последовательность {хn} называют ограниченной снизу, если все ее члены не меньше некоторого числа m.
- 45. Последовательность {хn} называют ограниченной снизу, если все ее члены не меньше некоторого числа m. Пример: 1,
- 46. Если последовательность ограничена и сверху и снизу, то ее называют ограниченной последовательностью.
- 47. Последовательность {хn} называют возрастающей последовательностью, если каждый ее член больше предыдущего. Пример: 1, 3, 5, 7,
- 49. Скачать презентацию







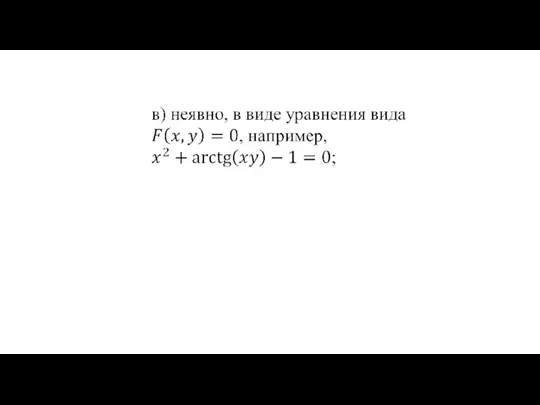








![Основные свойства функций: Монотонность Функция f(x) называется возрастающей на промежутке [a; b],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/951151/slide-18.jpg)
![Основные свойства функций: Монотонность Функция f(x) называется убывающей на промежутке [a; b],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/951151/slide-19.jpg)



![Основные свойства функций: Ограниченность Функция, ограниченная на [a, b] и сверху, и](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/951151/slide-23.jpg)

















 Алгебра высказываний
Алгебра высказываний Соотношения между сторонами и углами прямоугольного треугольника. Задачи на готовых чертежах
Соотношения между сторонами и углами прямоугольного треугольника. Задачи на готовых чертежах Тригонометрия. Итоговое повторение
Тригонометрия. Итоговое повторение ЛЕКЦИЯ_6
ЛЕКЦИЯ_6 Преобразование графиков функций
Преобразование графиков функций Статистический анализ данных. Первые шаги. Лекция 10
Статистический анализ данных. Первые шаги. Лекция 10 Презентация на тему Сечения
Презентация на тему Сечения  Властивості задачі лінійного програмування
Властивості задачі лінійного програмування Центральные и вписанные углы. Проверочная работа
Центральные и вписанные углы. Проверочная работа Симметрическая и знакопеременная группы. Алгебраические операции
Симметрическая и знакопеременная группы. Алгебраические операции Решение интеграла
Решение интеграла Многогранники. Призма
Многогранники. Призма Уравнения с одной переменной
Уравнения с одной переменной Развёртка, как основа объёмной конструкции
Развёртка, как основа объёмной конструкции Многомерные случайные величины
Многомерные случайные величины Цилиндр
Цилиндр Дроби. Десятичные дроби. Контрольный работа
Дроби. Десятичные дроби. Контрольный работа Презентация на тему Координаты на плоскости
Презентация на тему Координаты на плоскости  Замена переменных в двойных интегралах
Замена переменных в двойных интегралах Таблицы истинности элементы теории множеств и алгебры логики
Таблицы истинности элементы теории множеств и алгебры логики Тренажер. Примеры
Тренажер. Примеры 3
3 СДНФ и СКНФ — два представления булевой функции
СДНФ и СКНФ — два представления булевой функции Модуль числа. Уравнения и неравенства, содержащие модуль
Модуль числа. Уравнения и неравенства, содержащие модуль Движение, 9 класс
Движение, 9 класс Признаки подобия треугольников
Признаки подобия треугольников Выборки и выборочные распределения. Медикодемографические показатели. Применение математических методов
Выборки и выборочные распределения. Медикодемографические показатели. Применение математических методов Математические головоломки
Математические головоломки