1665470218901_Лекция Бернулли-1

Формула Бернулли
Пусть в результате испытания возможны два исхода: либо появление события А, либо противоположное ему событие Ấ. Проведем n независимых испытаний.
Обозначим вероятность Р(А) появление события А в единственном испытании буквой р, т.е. Р(А)=р, а вероятность Р(Ấ) – буквой q, т.е Р(Ấ)=1-р=q.
Найдем вероятность Рn(k) наступления события А ровно k раз в n независимых испытаниях.

Обозначим: Аi - появление события А в i – м опыте
i=1, 2, 3, …n.
Для n=1
Р1(1)=р, Р1(0)=q, р + q = 1
Для n=2
Р2(2)=р*р, P2(1)=q*р + р*q=2р*q, Р2(0)=q*q,
р² +2p*q + q² = (p+q)² = 1

Для n=3,
Р3(3)=р³, Р3(2)=3р²q, Р3(1)=3рq², Р3(0)=q³,
р³ + 3p²q + 3pq² + q³ = (p+q)³ = 1
Анализируя эти случаи, можно сделать общий вывод: вероятность Рn(k) пропорциональна произведению , причем коэффициент пропорциональности равен т.е.
Формула Бернулли

Задача 1.
Вероятность изготовления на станке нестандартной детали равна 0,02. Какова вероятность того, что среди наудачу взятых шести деталей окажется
а) четыре нестандартные
б) более четырех стандартных

Решение

Локальная теорема Муавра- Лапласа
Если вероятность наступления события А в каждом из n независимых испытаниях равна р и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность Рn(k) того, что в n испытаниях событие А наступит k раз, приближенно равна (чем больше n, тем точнее) значению функции , где

План нахождения Рn(k) по локальной теореме Муавра-Лапласа
Вычислить
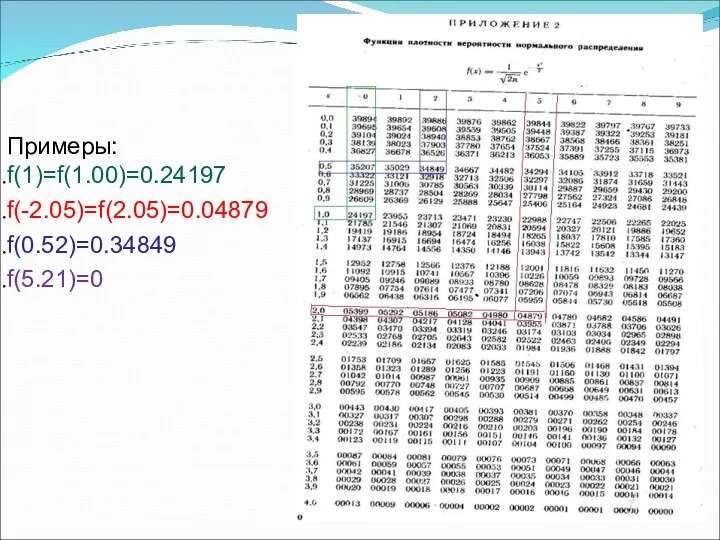
По приложению 2 найти
Вычислить
Свойства f(x):
f(-x)=f(x)
f (-∞) = f ( ∞) =0

Примеры:
f(1)=f(1.00)=0.24197
f(-2.05)=f(2.05)=0.04879
f(0.52)=0.34849
f(5.21)=0

Задача 2
Вероятность того, что сошедшая с конвейера деталь стандартная, равна 0,9. Найти вероятность того, что из 400 сошедших с конвейера деталей 356 окажутся стандартными.

Решение.

Интегральная теорема Муавра- Лапласа
Если вероятность р наступления события А в каждом из n независимом испытании равна отлична от нуля и единицы, то для вероятности Рn(k1, k2) того, событие А появится в n испытаниях от k1 до k2 раз, справедливо следующее соотношение:

План нахождения Рn(k1, k2) по интегральной теореме Муавра-Лапласа
Вычислить
По приложению 3 найти Ф(х1) и Ф(х2)
Вычислить
Свойства Ф(x):
Ф(-x)= 1- Ф(x)
Ф (-∞) = 0
Ф( ∞) =1

Примеры:
Ф(1)=Ф(1.00)=0.84134
Ф(-2.05)=1-Ф(2.05)=
=1-0,97982=0,02018
3. Ф(5.21)=1

Задача 3
Известно, что при контроле бракуется 10% изделий. На контроль отобрано 625 изделий. Какова вероятность того, что среди отобранных не менее 550 и не более 575 стандартных изделий?

Решение

Формула Пуассона
Если вероятность р наступления события А в каждом испытании постоянна, но близка к нулю, число независимых испытаний n достаточно велико, а произведение np=λ<10, то вероятность Рn(k) того, что в n испытаниях событие А наступит k раз, приближенно равна , ,т.е.
Формула Пуассона

План нахождения Рn(k) по формуле Пуассона
Вычислить n·p=λ
По приложению 1
найти Рn(k)

Задача 4
Устройство выходит из строя, если откажет определенная микросхема. Вероятность ее отказа в течении 1 ч. работы устройства равна 0,004. Какова вероятность того, что за 1000 ч. работы устройства придется пять раз менять микросхему?