Содержание
- 2. Исторические сведения. Дифференциальное исчисление создано Ньютоном и Лейбницем в конце 17 столетия. Понятие производной встречалось в
- 3. Таким образом, "новая" математика не отвечала стандартам строгости, привычным для ученых, воспитанных на классических образцах греческих
- 4. Темы 1.Определение производной. 2.Правила вычисления производной. 3.Производная сложной функции. 4. Физический Физический и геометрический смысл производной.
- 5. Производная Определение. Производной функции f в точке х0 называется число, к которому стремится отношение Операция нахождения
- 6. Правила вычисления производной Пусть u и v дифференцируемые функции, а с – const. Тогда
- 7. Производная сложной функции
- 8. Правила дифференцирования Правило 1: Если функции y=f(x) y=g(x) имеют производную в точке х, то и их
- 9. Правило 4: Если функции y=f(x) и y=g(x) имеют производную в точке х и в этой точке
- 10. Геометрический смысл производной Касательной к графику функции f(x) в точке х0 называется прямая, задаваемая уравнением α
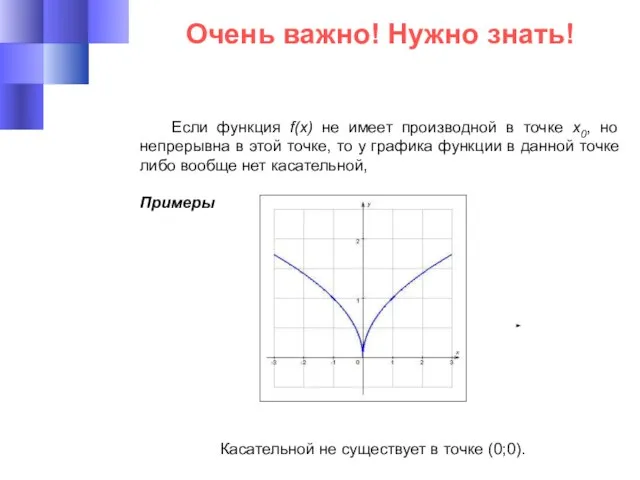
- 11. Очень важно! Нужно знать! Если функция f(x) не имеет производной в точке х0, но непрерывна в
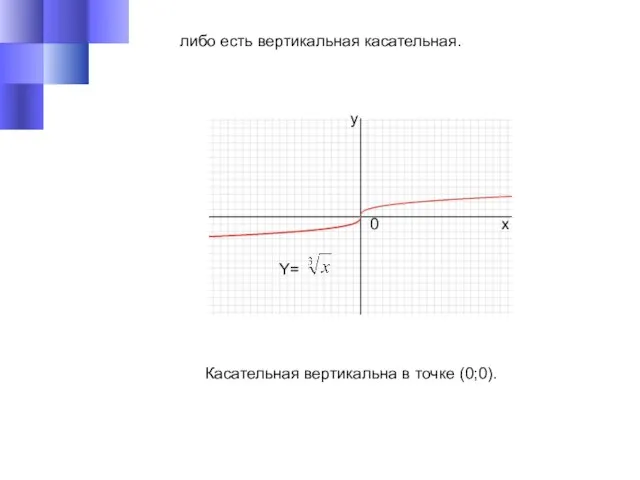
- 12. либо есть вертикальная касательная. Касательная вертикальна в точке (0;0). y x 0 Y=
- 13. Следовательно : Существование производной функции f в точке х0 эквивалентно существованию (невертикальной) касательной в точке (х0;
- 14. Физический смысл производной Пусть S=S(t) – зависимость пути от времени, тогда Скорость – производная пути по
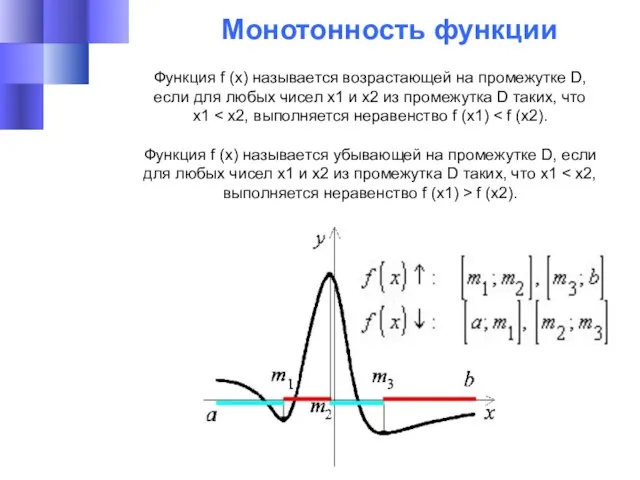
- 15. Монотонность функции Функция f (x) называется возрастающей на промежутке D, если для любых чисел x1 и
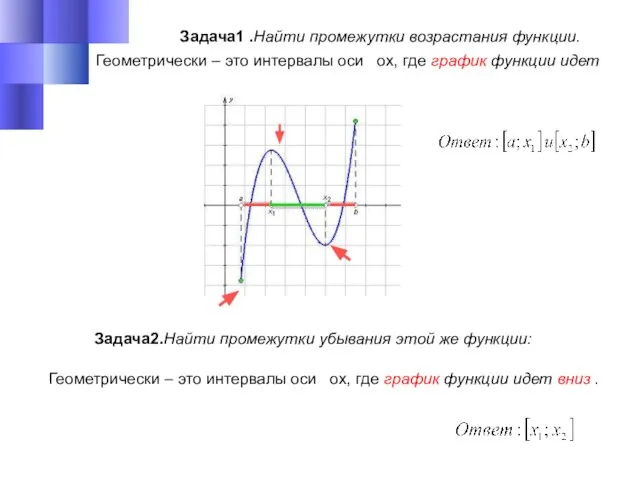
- 16. Геометрически – это интервалы оси ox, где график функции идет вверх. . Задача1 .Найти промежутки возрастания
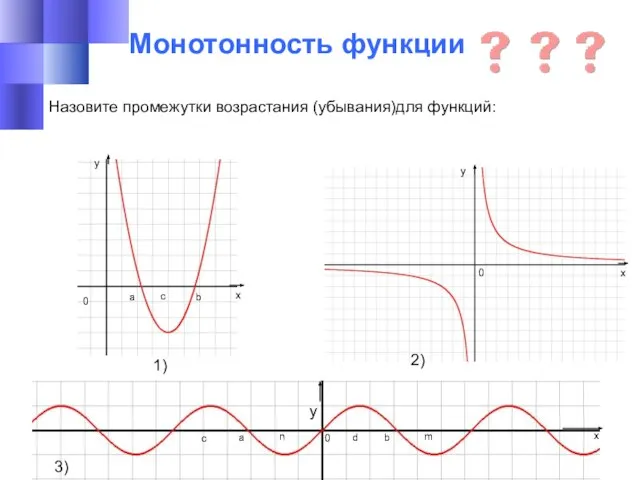
- 17. Монотонность функции Назовите промежутки возрастания (убывания)для функций: 0 0 a b c a b c d
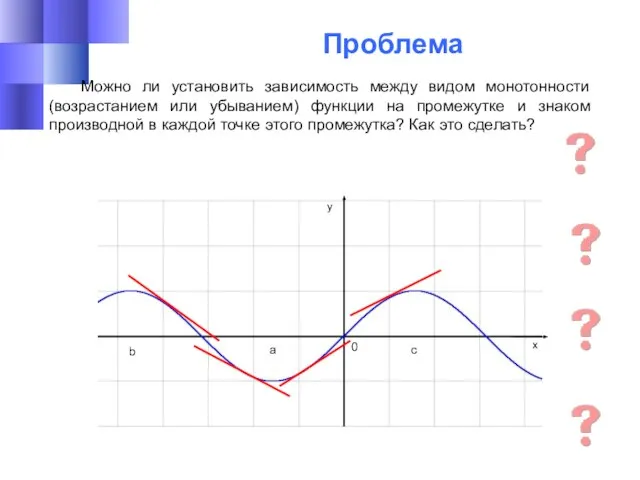
- 18. a b c 0 y x Проблема Можно ли установить зависимость между видом монотонности (возрастанием или
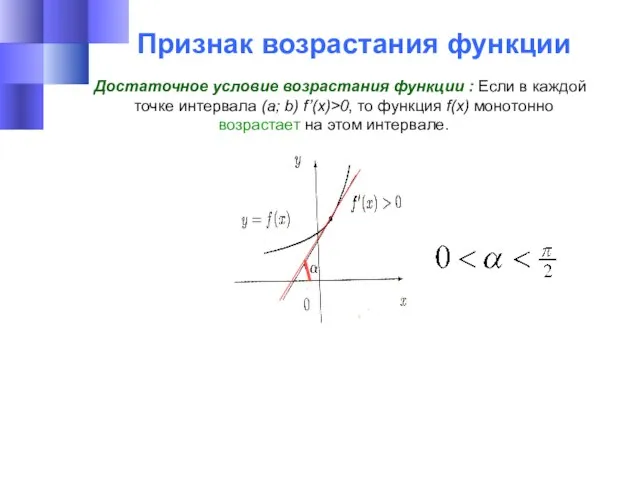
- 19. Признак возрастания функции Достаточное условие возрастания функции : Если в каждой точке интервала (a; b) f’(x)>0,
- 20. Признак убывания функции Достаточное условие убывания функции : Если в каждой точке интервала (a; b) f’(x)
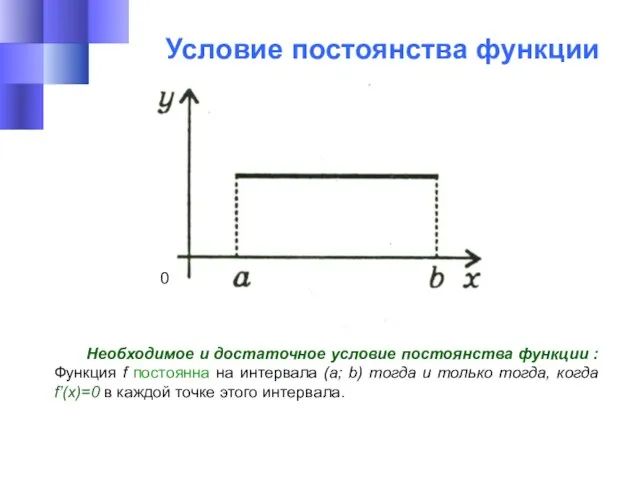
- 21. Условие постоянства функции Необходимое и достаточное условие постоянства функции : Функция f постоянна на интервала (a;
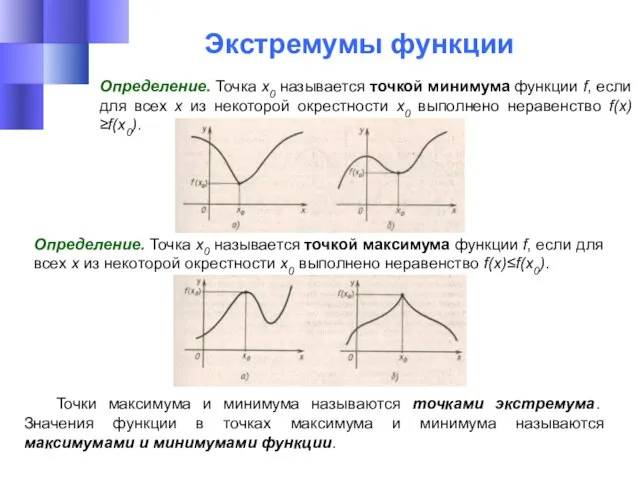
- 22. Экстремумы функции Определение. Точка х0 называется точкой максимума функции f, если для всех х из некоторой
- 23. Критические точки функции Определение. Внутренние точки области определения функции, в которых ее производная равна нулю или
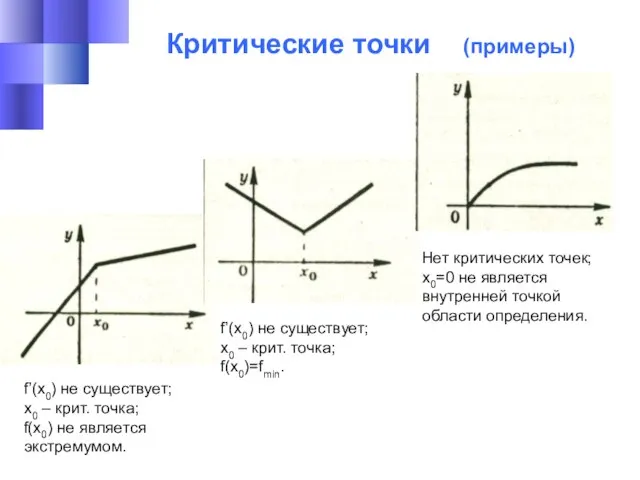
- 24. Критические точки (примеры) f’(x0) не существует; х0 – крит. точка; f(x0) не является экстремумом. f’(x0) не
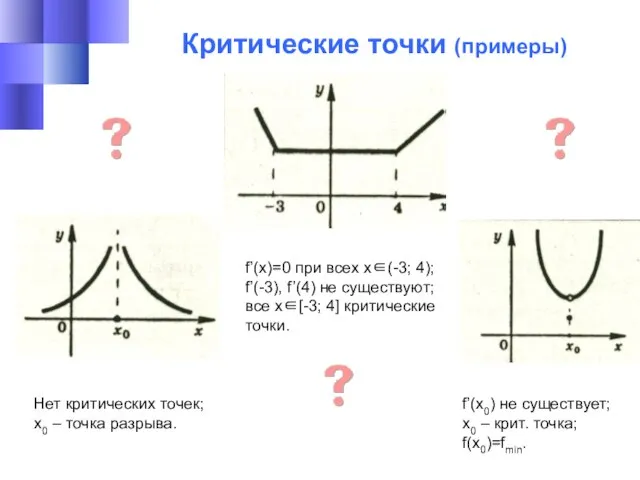
- 25. Критические точки (примеры) f’(x)=0 при всех x∈(-3; 4); f’(-3), f’(4) не существуют; все x∈[-3; 4] критические
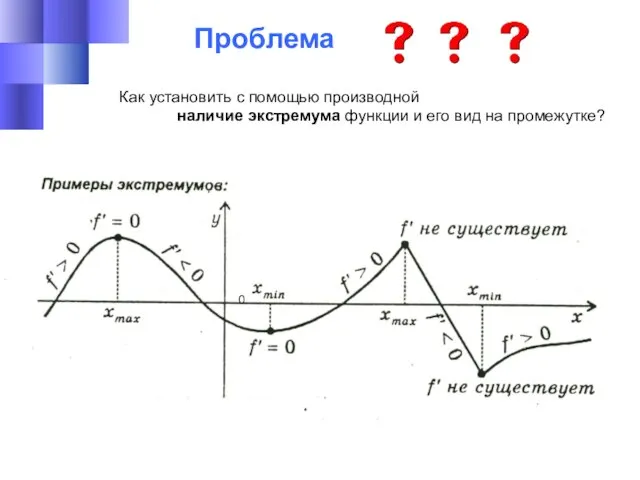
- 26. Проблема Как установить с помощью производной наличие экстремума функции и его вид на промежутке? 0
- 27. Достаточное условие экстремума Если функция f непрерывна в точке х0 и производная f’(x) меняет знак в
- 29. Скачать презентацию














 Вписанный угол
Вписанный угол Измеряй и сравнивай
Измеряй и сравнивай Решение заданий с производной
Решение заданий с производной Начальные геометрические сведения. Решение задач
Начальные геометрические сведения. Решение задач Стереометрия. Многогранники
Стереометрия. Многогранники Свойства умножения
Свойства умножения Число. Натуральный ряд. Абсолютная шкала измерений
Число. Натуральный ряд. Абсолютная шкала измерений Биржа знаний
Биржа знаний Урок систематизации и обобщения знаний, умений и навыков за курс математики 5 – 9 классов (4)
Урок систематизации и обобщения знаний, умений и навыков за курс математики 5 – 9 классов (4) Словарь Владимира Ивановича Даля
Словарь Владимира Ивановича Даля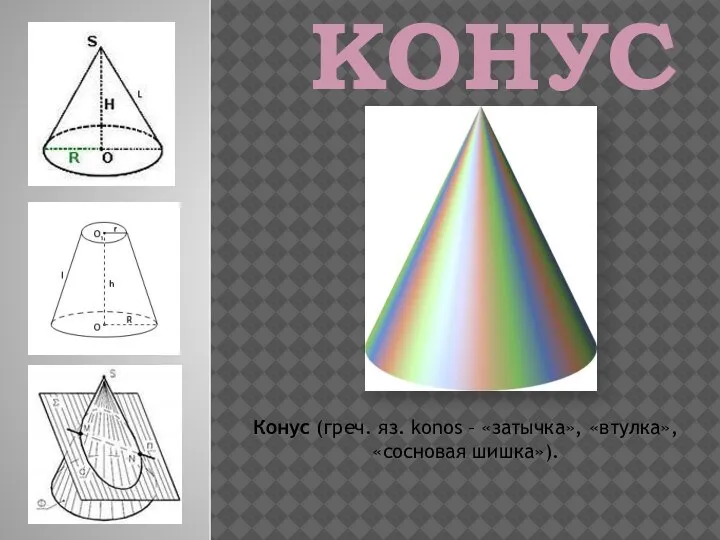 Конус. Виды конусов. Конусы в нашей жизни
Конус. Виды конусов. Конусы в нашей жизни Правило деления чисел на 1 и на само число
Правило деления чисел на 1 и на само число Введение понятия целого и дробного выражения
Введение понятия целого и дробного выражения Дифференцирование и интегрирование функций. ПМиПК-6
Дифференцирование и интегрирование функций. ПМиПК-6 Метод сложения
Метод сложения Презентация на тему Разложение многочлена на множители с помощью комбинации различных приемов
Презентация на тему Разложение многочлена на множители с помощью комбинации различных приемов  Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Функции. Свойства функций. Математический анализ
Функции. Свойства функций. Математический анализ Интегрирование неотрицательніх измериміх функций
Интегрирование неотрицательніх измериміх функций Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Своя игра. Показательная и степенная функции. 10 класс
Своя игра. Показательная и степенная функции. 10 класс урок 1, урок 2 9кл геом водный урок
урок 1, урок 2 9кл геом водный урок Соединения с повторениями
Соединения с повторениями Проецирование многогранных и кривых поверхностей
Проецирование многогранных и кривых поверхностей Полный факторный эксперимент (ПФЭ)
Полный факторный эксперимент (ПФЭ) Движение по окружности. Подборка задач
Движение по окружности. Подборка задач Основы математической статистики в метрологии. Часть 2
Основы математической статистики в метрологии. Часть 2 Единица длины миллиметр
Единица длины миллиметр