Содержание
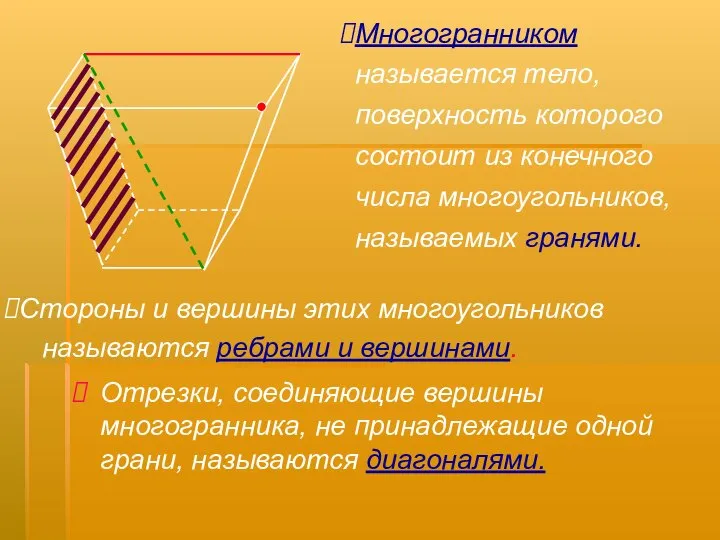
- 2. Отрезки, соединяющие вершины многогранника, не принадлежащие одной грани, называются диагоналями. Многогранником называется тело, поверхность которого состоит
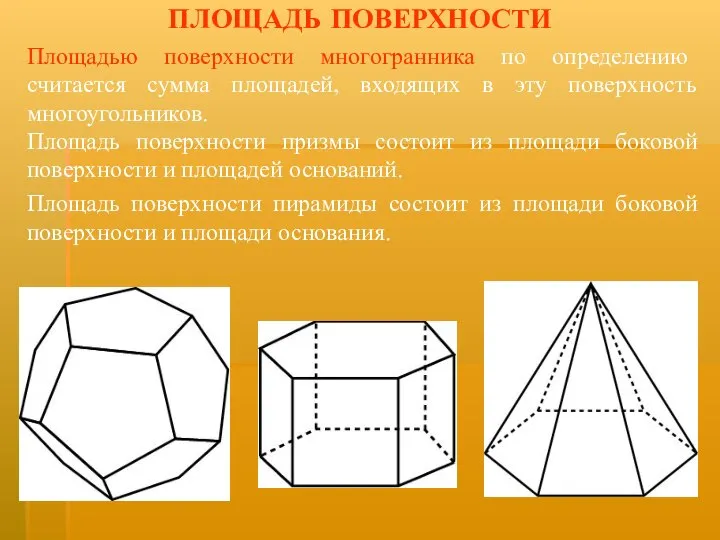
- 3. ПЛОЩАДЬ ПОВЕРХНОСТИ Площадью поверхности многогранника по определению считается сумма площадей, входящих в эту поверхность многоугольников. Площадь
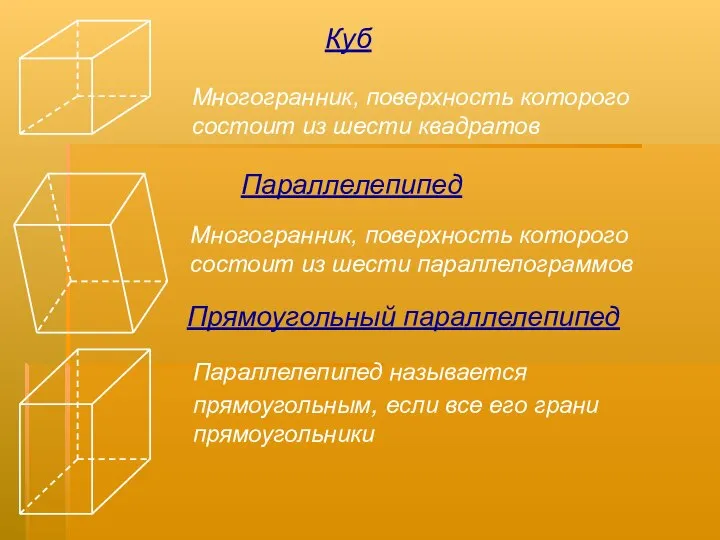
- 4. Многогранник, поверхность которого состоит из шести квадратов Многогранник, поверхность которого состоит из шести параллелограммов Параллелепипед называется
- 5. Площадь призмы Sбок. + 2Sосн Sбок. = Ph a b h Теорема: Площадь боковой поверхности прямой
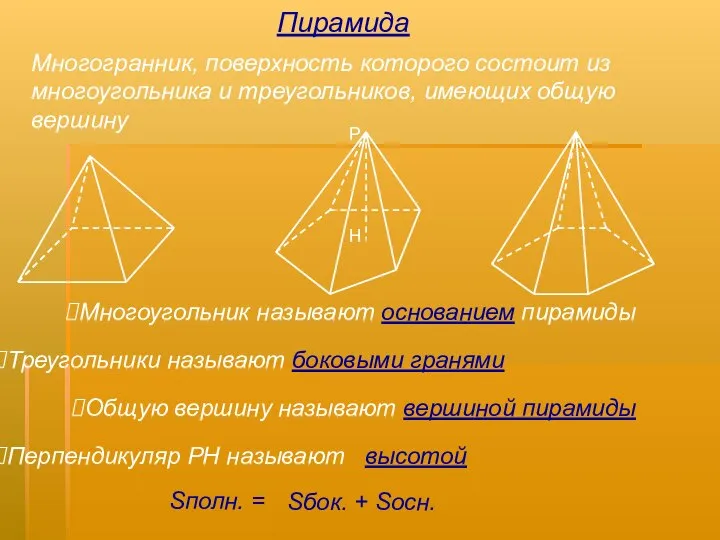
- 6. Многогранник, поверхность которого состоит из многоугольника и треугольников, имеющих общую вершину Многоугольник называют основанием пирамиды Треугольники
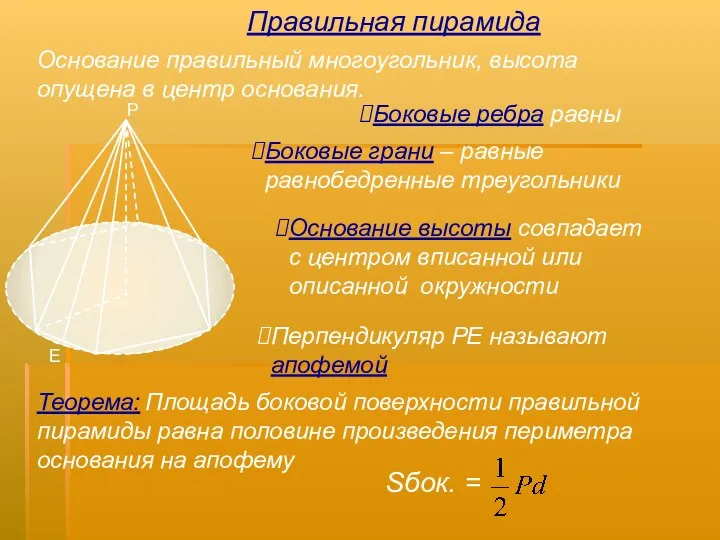
- 7. Основание правильный многоугольник, высота опущена в центр основания. Перпендикуляр РЕ называют апофемой Теорема: Площадь боковой поверхности
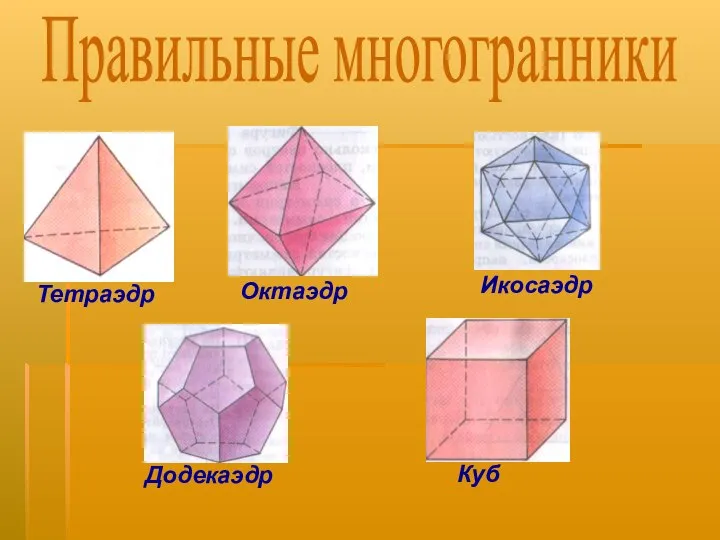
- 8. Правильные многогранники
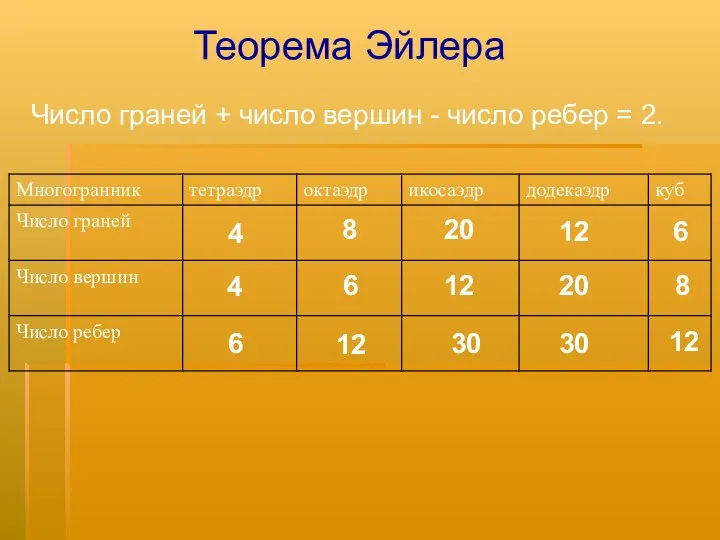
- 9. Теорема Эйлера Число граней + число вершин - число ребер = 2. 4 4 6 8
- 10. Площадь поверхности цилиндра. O Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами AB – образующая,
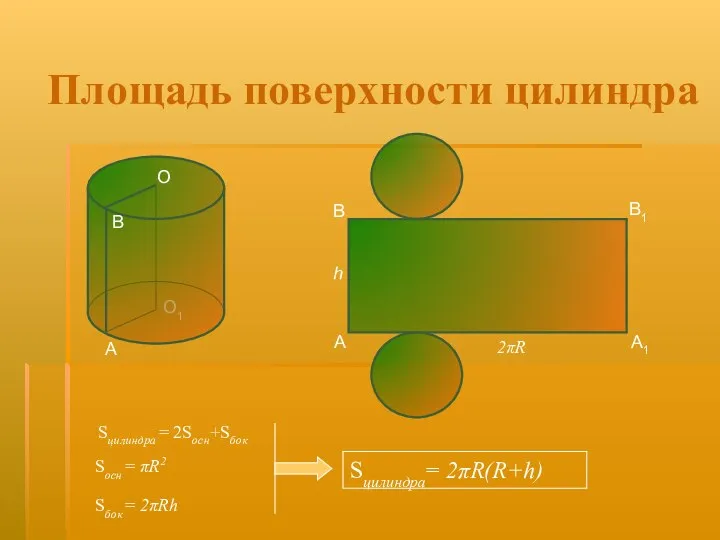
- 11. Площадь поверхности цилиндра Sцилиндра = 2Sосн+Sбок Sцилиндра= 2πR(R+h) O Sосн = πR2 Sбок = 2πRh
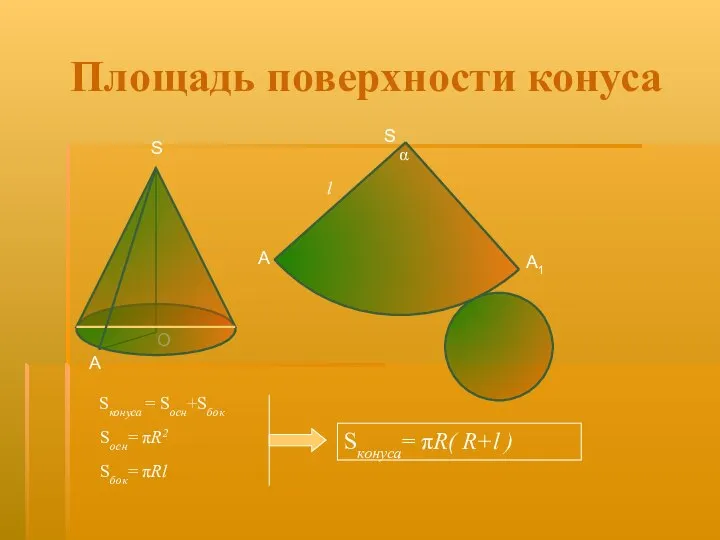
- 12. Площадь поверхности конуса Конус – тело, ограниченное конической поверхностью и кругом. SA – образующая конуса SO
- 13. O A S Площадь поверхности конуса Sконуса = Sосн+Sбок Sконуса= πR( R+l ) Sосн= πR2 Sбок=
- 14. Площадь поверхности сферы Сфера – поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от
- 15. Площадь поверхности сферы Sсферы = 4πR2
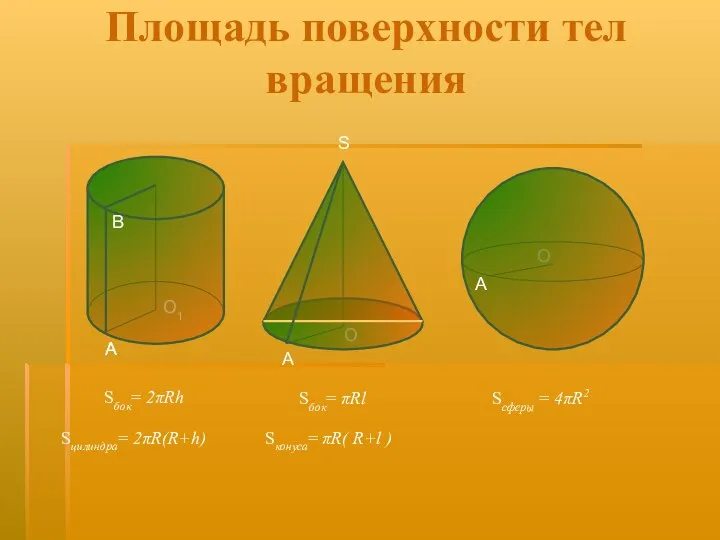
- 16. Площадь поверхности тел вращения Sбок= 2πRh Sцилиндра= 2πR(R+h) Sбок= πRl Sконуса= πR( R+l ) Sсферы =
- 17. Упражнение 1 Чему равна площадь поверхности куба с ребром 1? Ответ: 6.
- 18. Упражнение 2 Объем куба равен 8 м3. Найдите площадь его поверхности. Ответ: 24 м2.
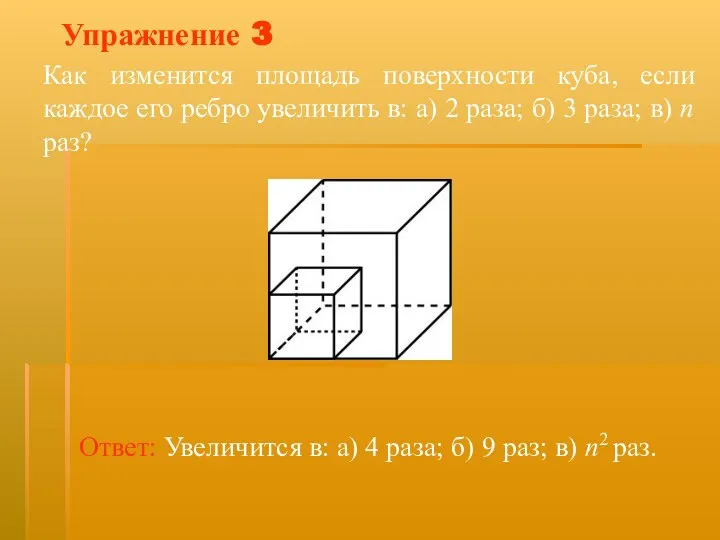
- 19. Упражнение 3 Как изменится площадь поверхности куба, если каждое его ребро увеличить в: а) 2 раза;
- 20. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Упражнение 6
- 21. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Упражнение 7
- 22. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Упражнение 8
- 23. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Упражнение 9
- 24. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Упражнение 10
- 25. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Упражнение 11
- 26. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Ответ. 48. Упражнение 12
- 27. В каждой грани куба с ребром 6 см проделали сквозное квадратное отверстие со стороной квадрата 2
- 28. Упражнение 14 Чему равна площадь поверхности правильного тетраэдра с ребром 1?
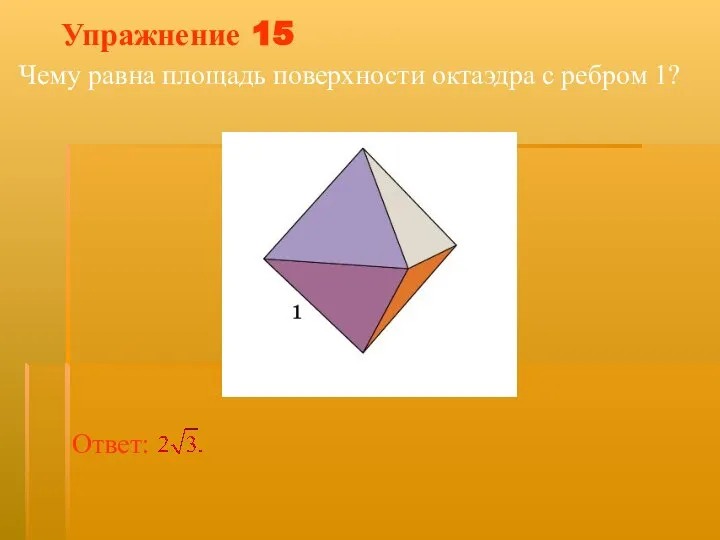
- 29. Упражнение 15 Чему равна площадь поверхности октаэдра с ребром 1?
- 30. Упражнение 16 Чему равна площадь поверхности икосаэдра с ребром 1?
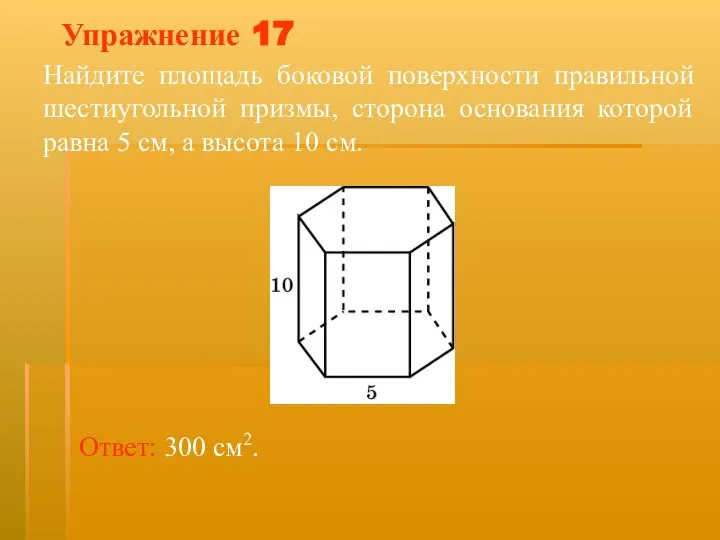
- 31. Упражнение 17 Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5 см, а
- 32. Упражнение 18 Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 см и 4 см,
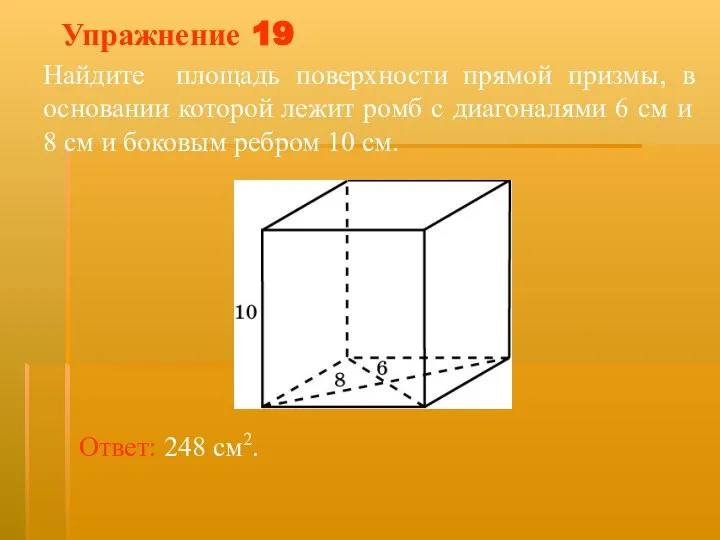
- 33. Упражнение 19 Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями 6 см
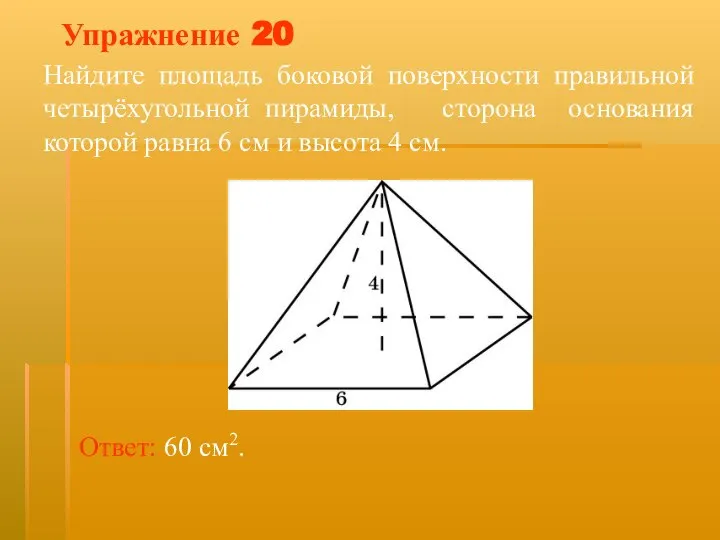
- 34. Упражнение 20 Найдите площадь боковой поверхности правильной четырёхугольной пирамиды, сторона основания которой равна 6 см и
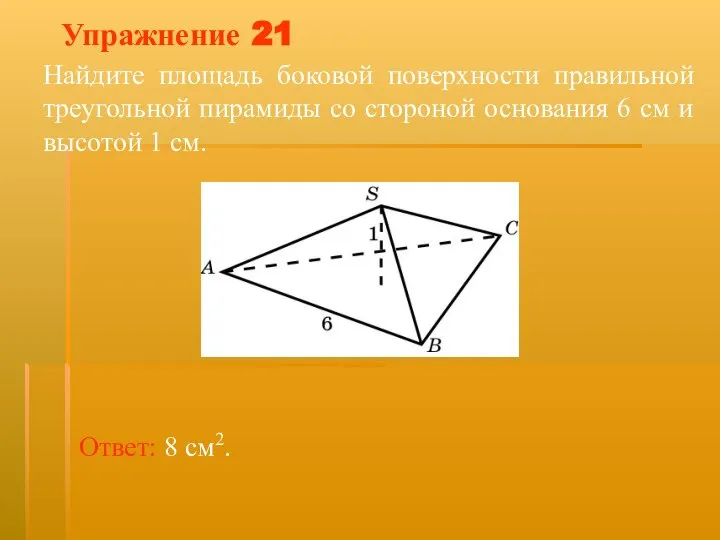
- 35. Упражнение 21 Найдите площадь боковой поверхности правильной треугольной пирамиды со стороной основания 6 см и высотой
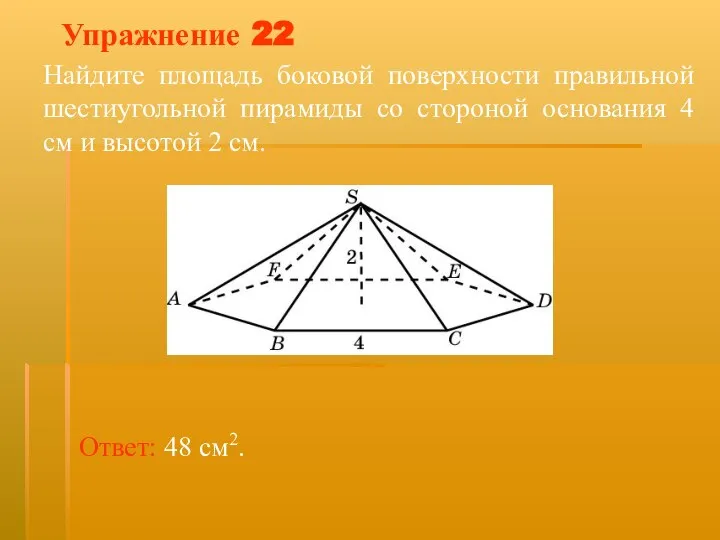
- 36. Упражнение 22 Найдите площадь боковой поверхности правильной шестиугольной пирамиды со стороной основания 4 см и высотой
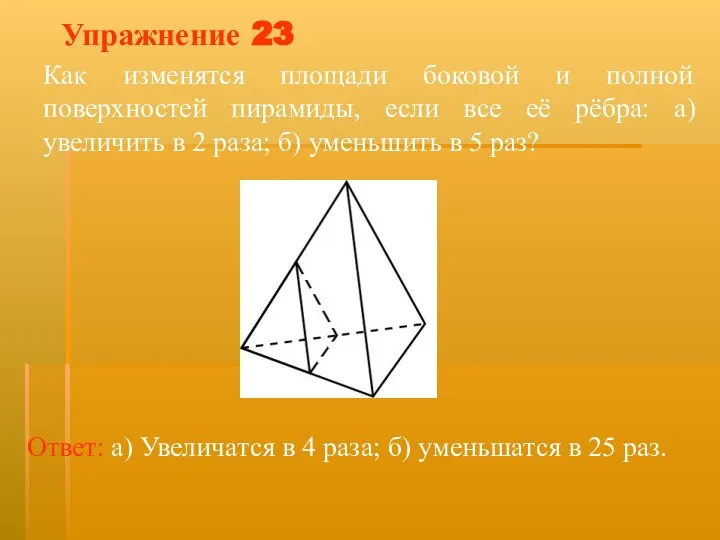
- 37. Упражнение 23 Как изменятся площади боковой и полной поверхностей пирамиды, если все её рёбра: а) увеличить
- 38. Упражнение 24 Развёртка поверхности правильной треугольной пирамиды представляет собой равносторонний треугольник, площадь которого равна 80 см2.
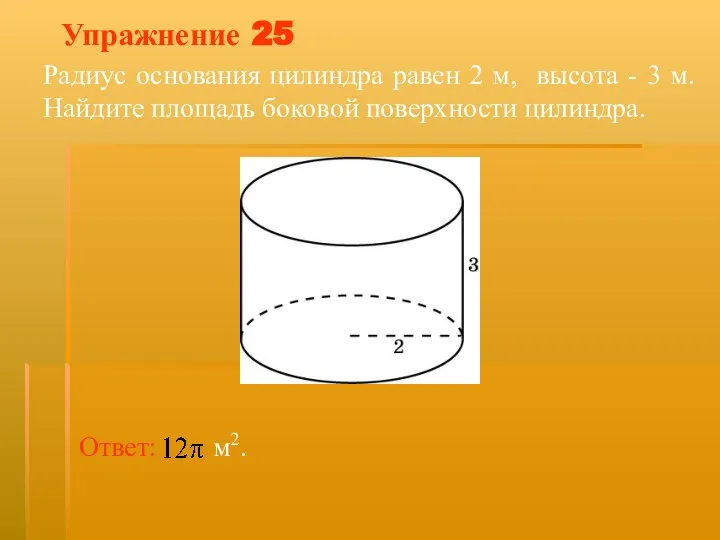
- 39. Упражнение 25 Радиус основания цилиндра равен 2 м, высота - 3 м. Найдите площадь боковой поверхности
- 40. Упражнение 26 Площадь осевого сечения цилиндра равна 4 м2. Найдите площадь боковой поверхности цилиндра.
- 41. Упражнение 27 Осевое сечение цилиндра - квадрат. Площадь основания равна 1. Найдите площадь поверхности цилиндра. Ответ:
- 42. Упражнение 28 Площадь боковой поверхности и объем цилиндра выражаются одним и тем же числом. Найдите диаметр
- 43. Упражнение 29 Два цилиндра образованы вращением одного и того же прямоугольника вокруг его неравных сторон. Равны
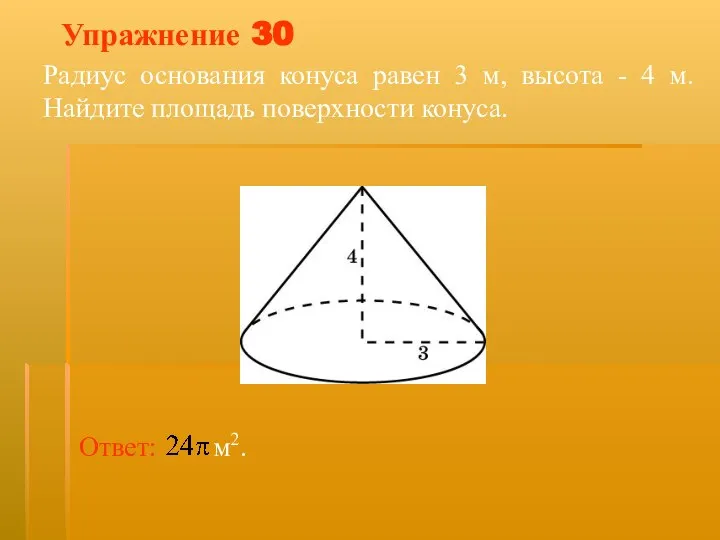
- 44. Упражнение 30 Радиус основания конуса равен 3 м, высота - 4 м. Найдите площадь поверхности конуса.
- 45. Упражнение 31 Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей
- 46. Упражнение 32 Образующая конуса равна 4 дм, а угол при вершине осевого сечения равен 90о. Вычислите
- 47. Упражнение 33 Два конуса образованы вращением одного и того же прямоугольного треугольника вокруг его неравных катетов.
- 49. Скачать презентацию


























 Комплексные числа и координатная плоскость. Решение примеров на построение комплексных чисел на комплексной плоскости
Комплексные числа и координатная плоскость. Решение примеров на построение комплексных чисел на комплексной плоскости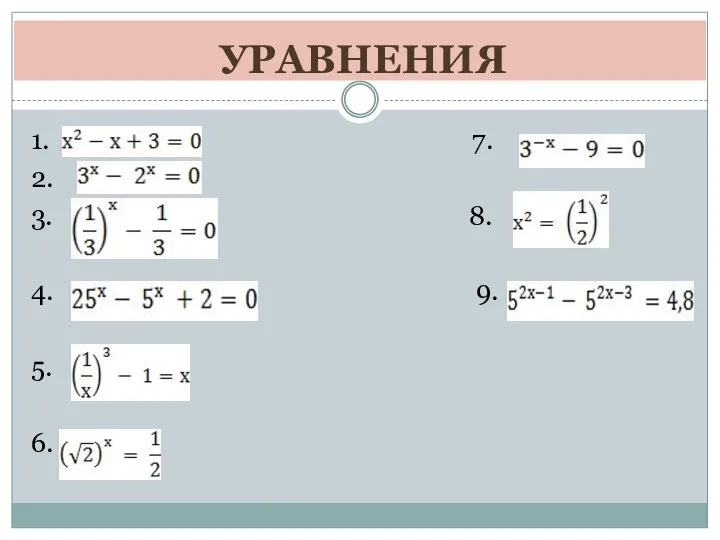 Решение показателей уравнений
Решение показателей уравнений Римские числа
Римские числа Повторительно-обобщающий урок по теме: Показательная функция. 11 класс
Повторительно-обобщающий урок по теме: Показательная функция. 11 класс Теоремы о пределах. Нахождение пределов
Теоремы о пределах. Нахождение пределов Презентация на тему Средняя линия треугольника
Презентация на тему Средняя линия треугольника  Реши примеры устно. 2 класс
Реши примеры устно. 2 класс Декартова система координат
Декартова система координат Презентация на тему Математический КВН
Презентация на тему Математический КВН  Отображения (функции)
Отображения (функции) Диалектика как методология научного познания
Диалектика как методология научного познания Экологические понятия в математике
Экологические понятия в математике Треугольники. Геометрия, 7 класс
Треугольники. Геометрия, 7 класс ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА Параллельные прямые. 7 класс
Параллельные прямые. 7 класс Научные открытия России. Задача тысячелетия. Теорема Пуанкаре
Научные открытия России. Задача тысячелетия. Теорема Пуанкаре Дифференциальные уравнения и их применение в медицине
Дифференциальные уравнения и их применение в медицине Динамика системы вблизи цикла
Динамика системы вблизи цикла Деление с остатком
Деление с остатком Парная линейная регрессия
Парная линейная регрессия Компоненти дій
Компоненти дій Фигуры вращения
Фигуры вращения Элементы комбинаторики. Решение простейших комбинаторных задач
Элементы комбинаторики. Решение простейших комбинаторных задач Таблица умножения с 7 до 9
Таблица умножения с 7 до 9 Производная и первообразная
Производная и первообразная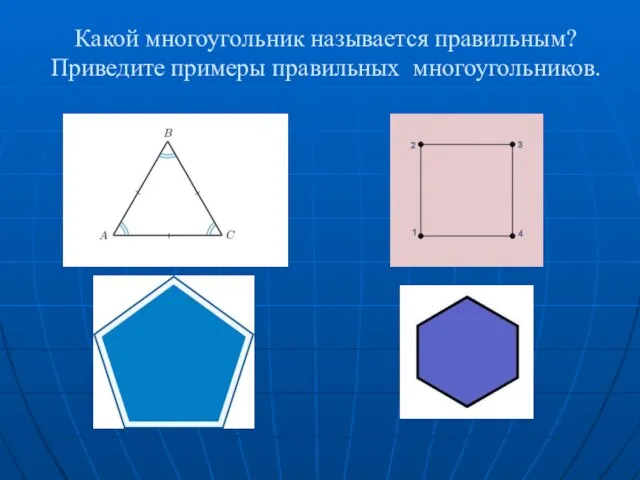 Какой многоугольник называется правильным? Приведите примеры правильных многоугольников
Какой многоугольник называется правильным? Приведите примеры правильных многоугольников Занимательные задачи
Занимательные задачи Основное свойство дроби
Основное свойство дроби