Содержание
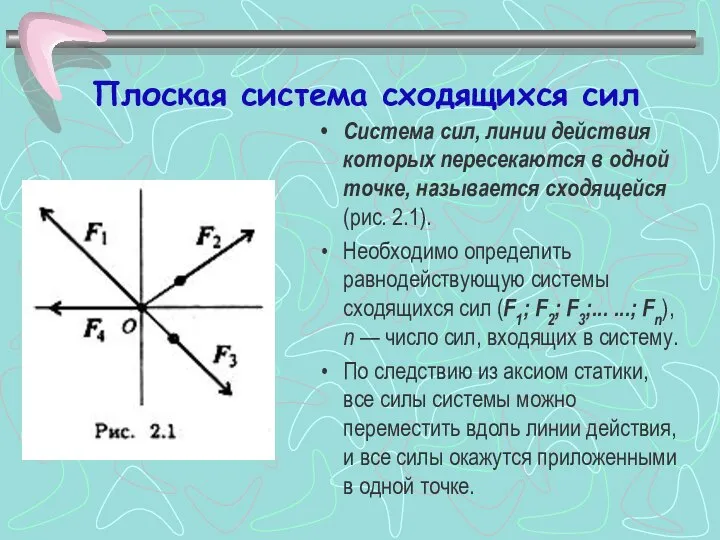
- 2. Плоская система сходящихся сил Система сил, линии действия которых пересекаются в одной точке, называется сходящейся (рис.
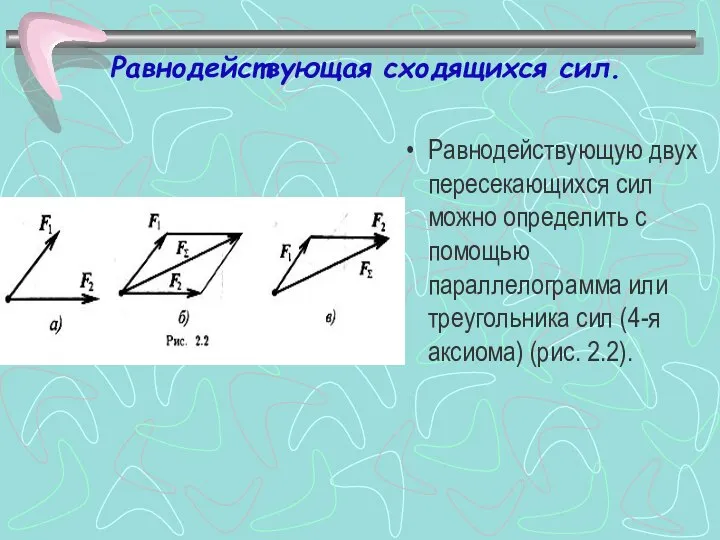
- 3. Равнодействующая сходящихся сил. Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника сил (4-я
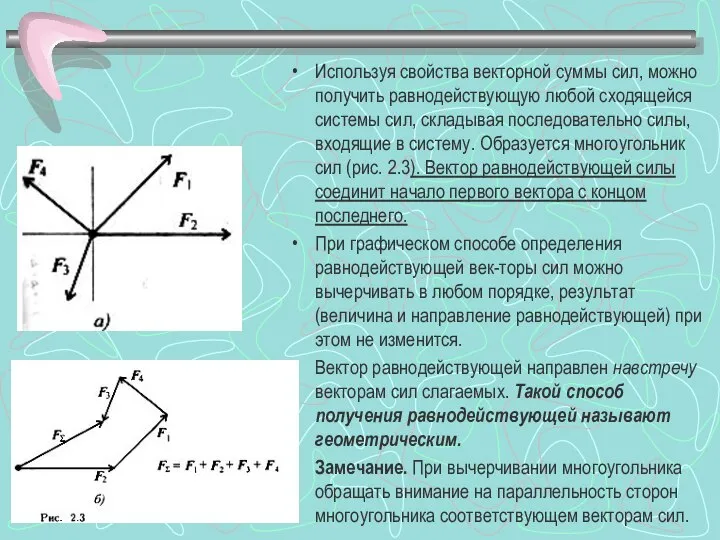
- 4. Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие
- 5. Порядок построения многоугольника сил: Вычертить векторы сил заданной системы в некотором масштабе один за другим так,
- 6. Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно,
- 7. Решение задач на равновесие геометрическим способом Порядок решения задач: Определить возможное направление реакций связей. Вычертить многоугольник
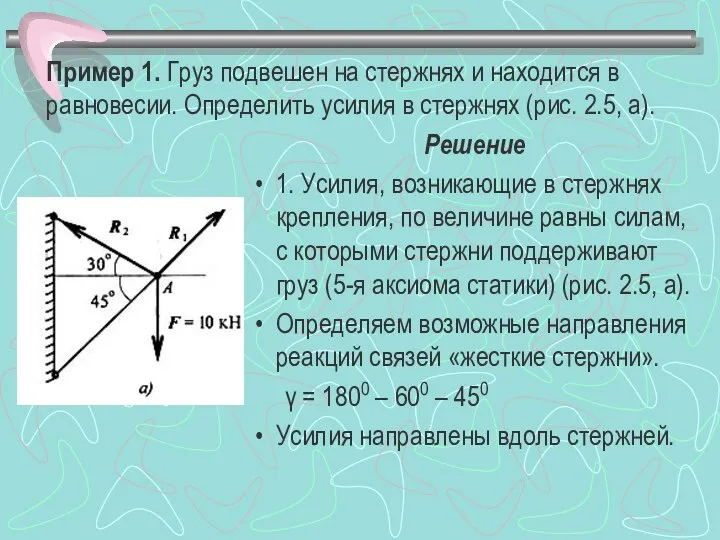
- 8. Пример 1. Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях (рис. 2.5,
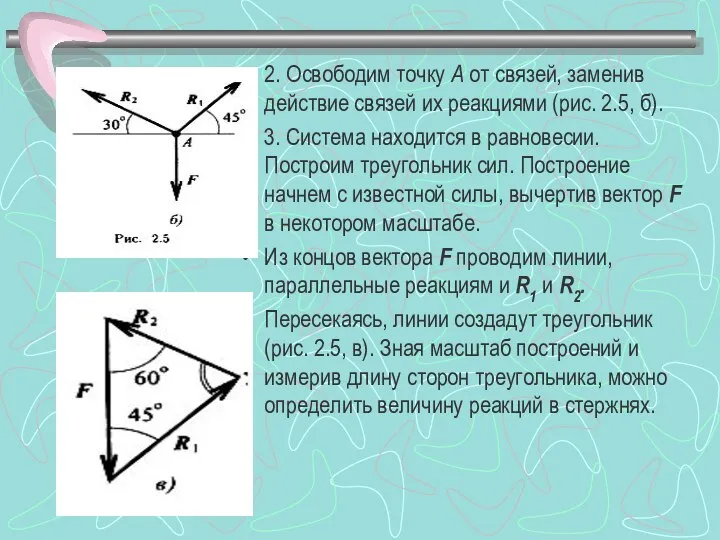
- 9. 2. Освободим точку А от связей, заменив действие связей их реакциями (рис. 2.5, б). 3. Система
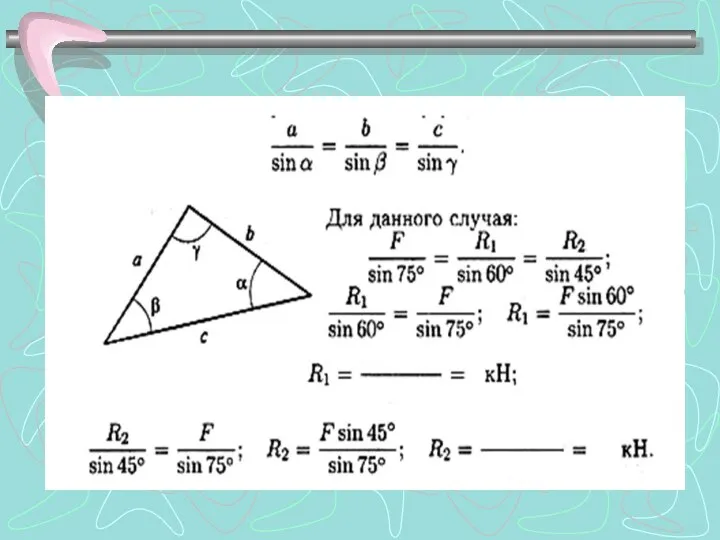
- 11. Для более точных расчетов можно воспользоваться геометрическими соотношениями, в частности теоремой синусов: отношение стороны треугольника к
- 12. Пример 2. Груз подвешен на стержнях и канатах и находится в равновесии. Определить усилия в стержнях
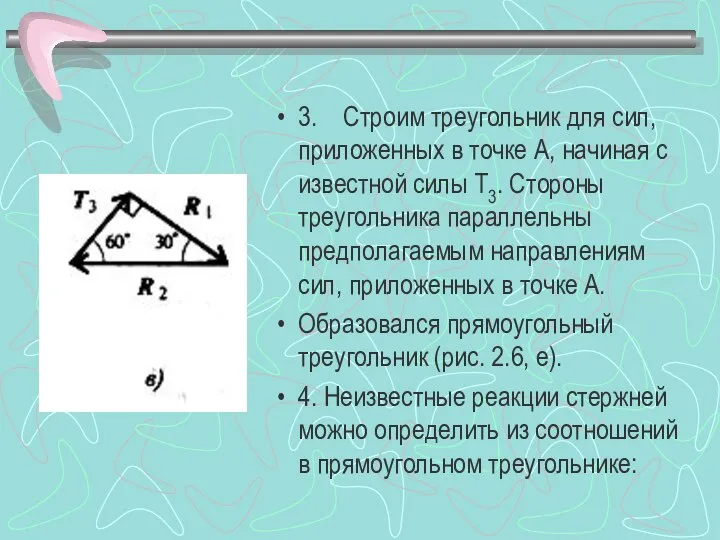
- 13. 3. Строим треугольник для сил, приложенных в точке А, начиная с известной силы Т3. Стороны треугольника
- 15. Скачать презентацию





 Ряды Тейлора. Применение степенных рядов
Ряды Тейлора. Применение степенных рядов Площадь параллелограмма
Площадь параллелограмма Организация исследовательской деятельности учащихся по математике
Организация исследовательской деятельности учащихся по математике Сравнение моделей
Сравнение моделей На лесной поляне
На лесной поляне Решение задач. Повторение пройденного
Решение задач. Повторение пройденного Операции над графами. (Лекция 7)
Операции над графами. (Лекция 7) Школа волшебников
Школа волшебников Методы составления уравнений неголономной механики в задаче волнового твердотельного гироскопа
Методы составления уравнений неголономной механики в задаче волнового твердотельного гироскопа Окружность и круг
Окружность и круг Подготовка к экзамену. Решение уравнений и неравенств
Подготовка к экзамену. Решение уравнений и неравенств Рівняння руху гіроскопу в кардановому підвісі
Рівняння руху гіроскопу в кардановому підвісі Циклоида, эпициклоида
Циклоида, эпициклоида Подумай. Вопросы. Тесты
Подумай. Вопросы. Тесты Таблица умножения и деления с числом 3
Таблица умножения и деления с числом 3 Понятие и виды средних величин
Понятие и виды средних величин Элементы теории случайных процессов
Элементы теории случайных процессов Вычисление площадей плоских фигур
Вычисление площадей плоских фигур Сечение поверхности плоскостью
Сечение поверхности плоскостью Правильный восьмиугольник
Правильный восьмиугольник Скалярное произведение векторов
Скалярное произведение векторов Неполные квадратные уравнения
Неполные квадратные уравнения Неравенства с двумя переменными и их системы
Неравенства с двумя переменными и их системы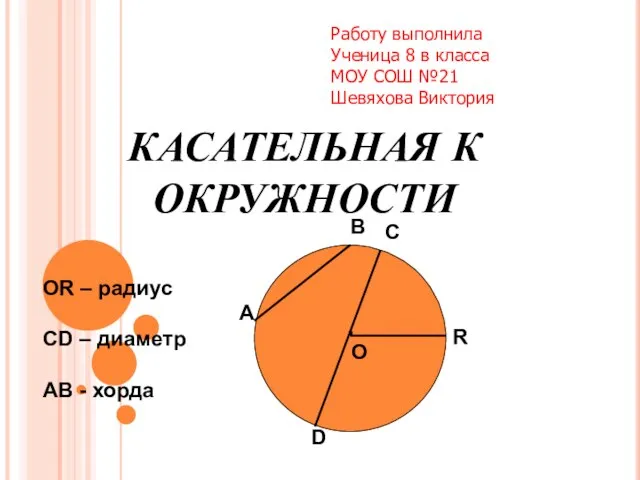 Презентация на тему Касательная к окружности
Презентация на тему Касательная к окружности  Сравнение групп предметов
Сравнение групп предметов Порядок выполнения действий
Порядок выполнения действий Показательные уравнения и неравенства
Показательные уравнения и неравенства Числовые великаны вокруг и внутри нас
Числовые великаны вокруг и внутри нас