Презентация на тему Площадь многоугольников

Проверка знаний
Заштриховать квадраты, в которых указаны неверные утверждения

Пифагор и его
теорема
Найдите правильную
формулировку теоремы Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме катетов
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
В прямоугольном треугольнике гипотенуза равна сумме квадратов катетов

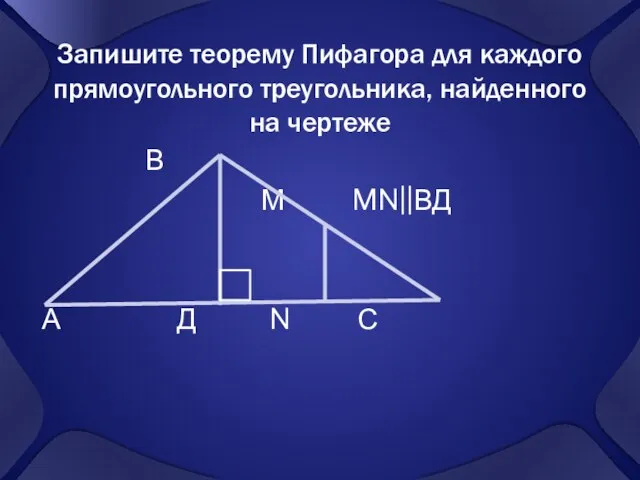
Запишите теорему Пифагора для каждого прямоугольного треугольника, найденного на чертеже
В
М MN||ВД
А Д N С

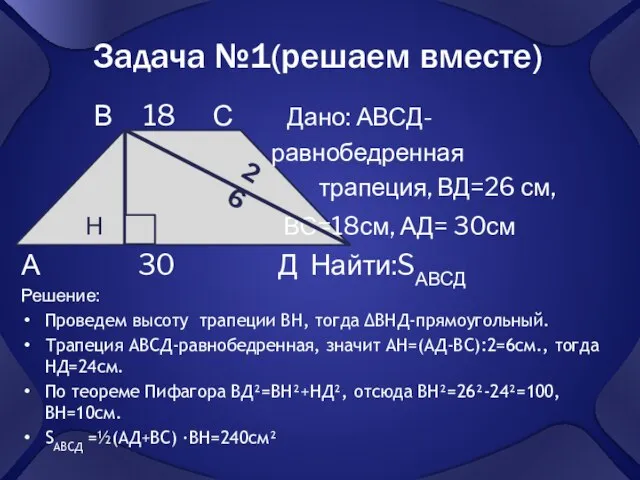
Задача №1(решаем вместе)
В 18 С Дано: АВСД-
равнобедренная
трапеция, ВД=26 см,
Н ВС=18см, АД= 30см
А 30 Д Найти:SАВСД
Решение:
Проведем высоту трапеции ВН, тогда ∆ВНД-прямоугольный.
Трапеция АВСД-равнобедренная, значит АН=(АД-ВС):2=6см., тогда НД=24см.
По теореме Пифагора ВД²=ВН²+НД², отсюда ВН²=26²-24²=100, ВН=10см.
SАВСД =½(АД+ВС) ·ВН=240см²
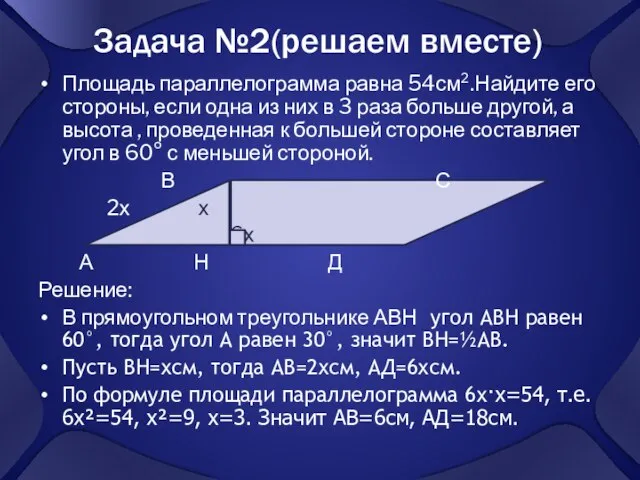
26

Задача №2(решаем вместе)
Площадь параллелограмма равна 54см².Найдите его стороны, если одна из них в 3 раза больше другой, а высота , проведенная к большей стороне составляет угол в 60° с меньшей стороной.
В С
2х х
6х
А Н Д
Решение:
В прямоугольном треугольнике АВН угол АВН равен 60°, тогда угол А равен 30°, значит ВН=½АВ.
Пусть ВН=хсм, тогда АВ=2хсм, АД=6хсм.
По формуле площади параллелограмма 6х·х=54, т.е. 6х²=54, х²=9, х=3. Значит АВ=6см, АД=18см.

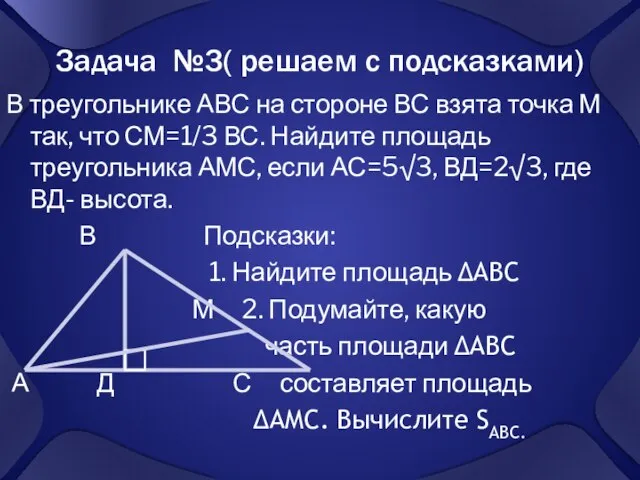
Задача №3( решаем с подсказками)
В треугольнике АВС на стороне ВС взята точка М так, что СМ=1/3 ВС. Найдите площадь треугольника АМС, если АС=5√3, ВД=2√3, где ВД- высота.
В Подсказки:
1. Найдите площадь ∆АВС
М 2. Подумайте, какую
часть площади ∆АВС
А Д С составляет площадь
∆АМС. Вычислите SАВС.

Домашнее задание
№502 площадь параллелограмма
( с помощью уравнения)
№ 492 площадь треугольника
№518 (а) площадь трапеции
Подготовка к контрольной работе

Самостоятельная работа
(на рабочих листах)
Ответы:
I вариант: 1) 42,5см²; 2) 13см и 14 см.
II вариант: 1) 56см²; 2) 20см и 48 см.
III вариант:1) 36см²; 2)S=80см², 4√5 и 8√5
IV вариант: 1) ОМ²=ОК²+КМ², МК=8см;
2) 48см².