Чертежи и развертки простых геометрических тел

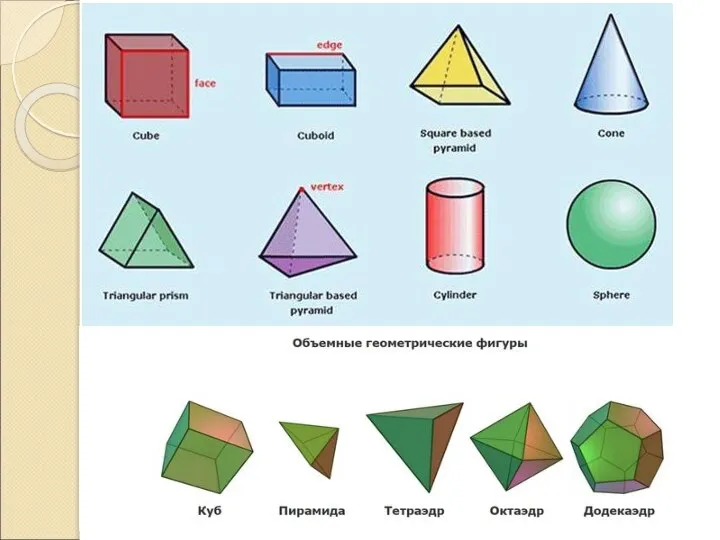
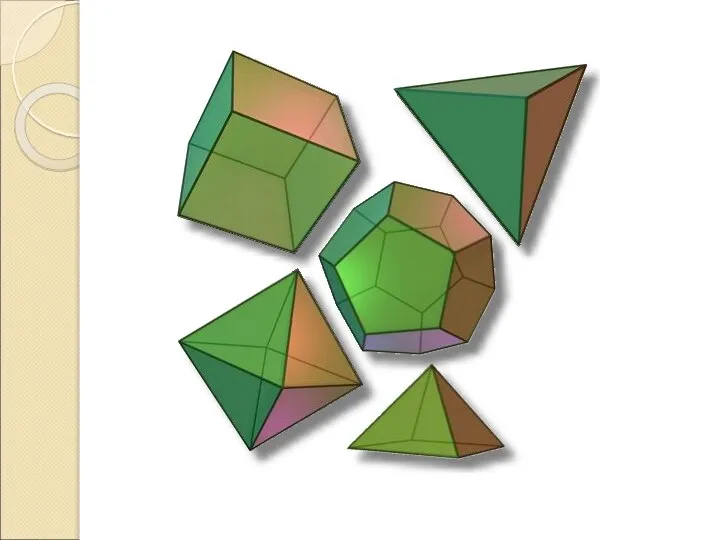
Моделирование из бумаги макетов геометрических тел

РАЗВЕРТКА
С развёртками поверхностей мы часто встречаемся в обыденной жизни, на производстве, в строительстве. Чтобы изготовить упаковку для сока, конфет, духов, праздничную коробочку или кулёк и т.п., надо уметь строить развёртки поверхностей геометрических тел.

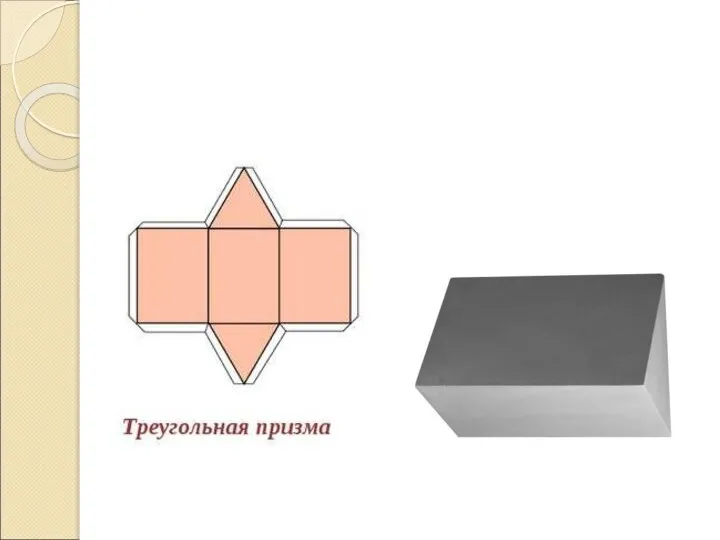
«Развёртка» - представляет собой плоский многоугольник, состоящий из меньших многоугольников – граней исходного многогранника.

Изготовление развертки
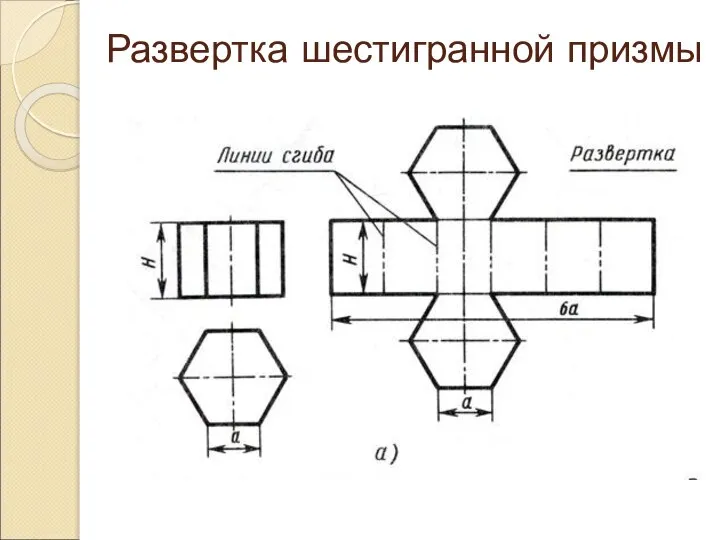
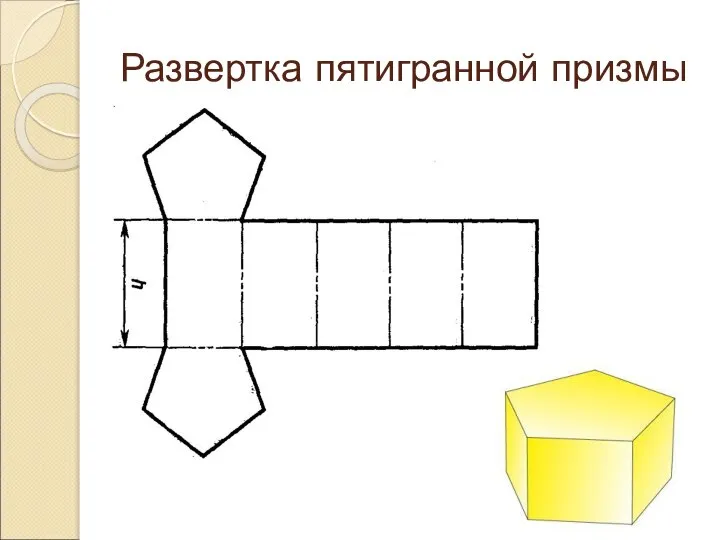
Изготовить объемное тело при помощи развертки можно, вычертив необходимое количество фигур, соединённых между собой линиями сгиба (штрихпунктирная с двумя точками) и равных сторонами (гранями) этого объемного тела

Инструменты и материалы, необходимые для выполнения макетов геометрических тел

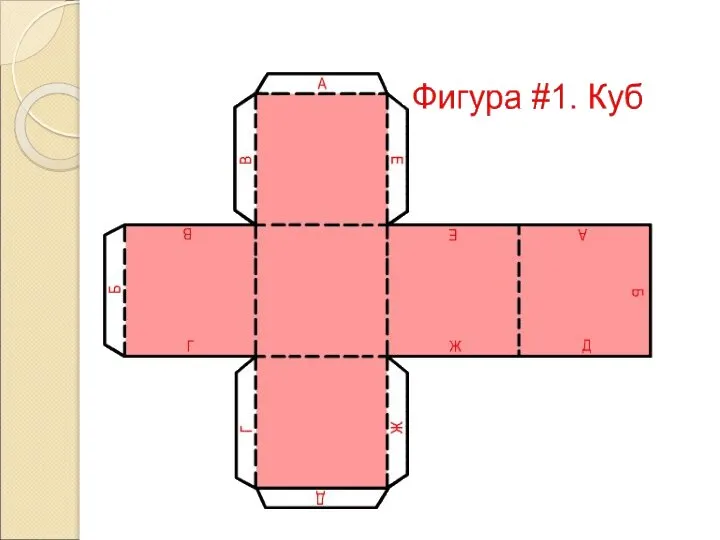
Развертка КУБА
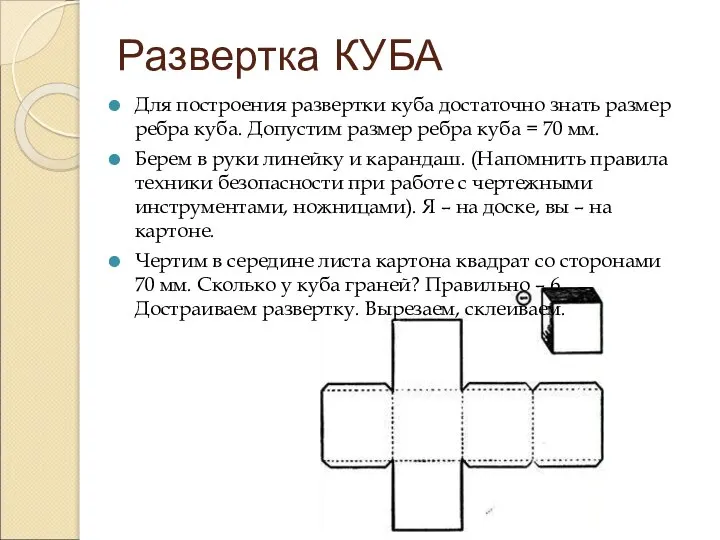
Для построения развертки куба достаточно знать размер ребра куба. Допустим размер ребра куба = 70 мм.
Берем в руки линейку и карандаш. (Напомнить правила техники безопасности при работе с чертежными инструментами, ножницами). Я – на доске, вы – на картоне.
Чертим в середине листа картона квадрат со сторонами 70 мм. Сколько у куба граней? Правильно – 6. Достраиваем развертку. Вырезаем, склеиваем.

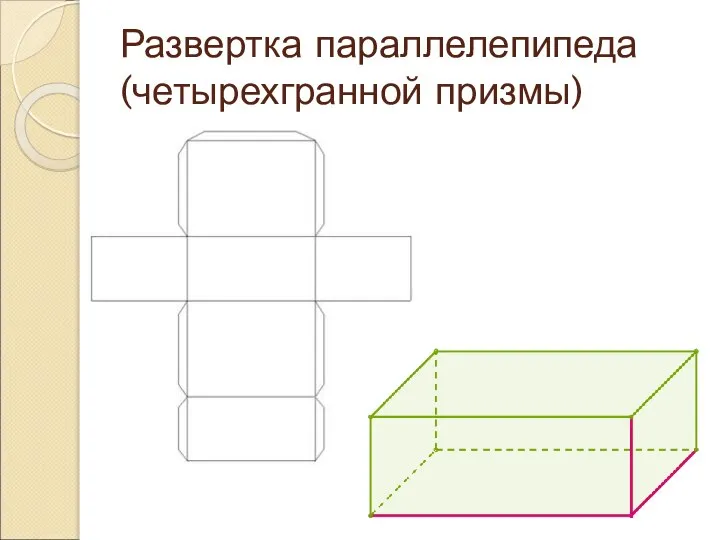
Развертка параллелепипеда (четырехгранной призмы)

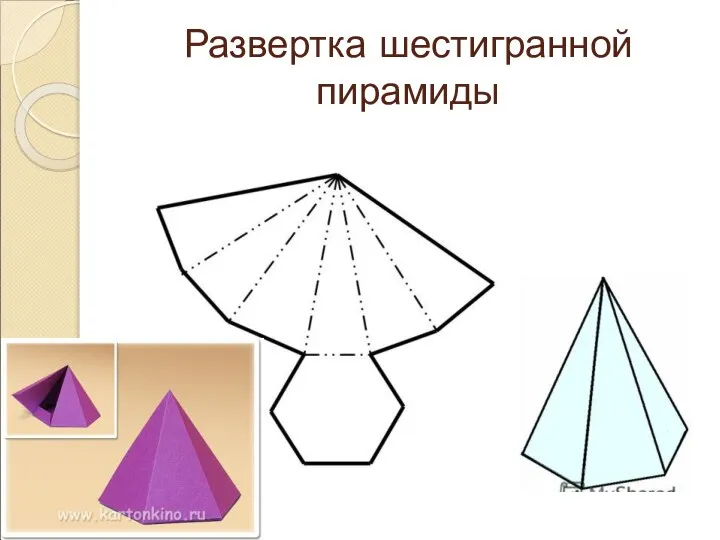
Развертка ПИРАМИДЫ
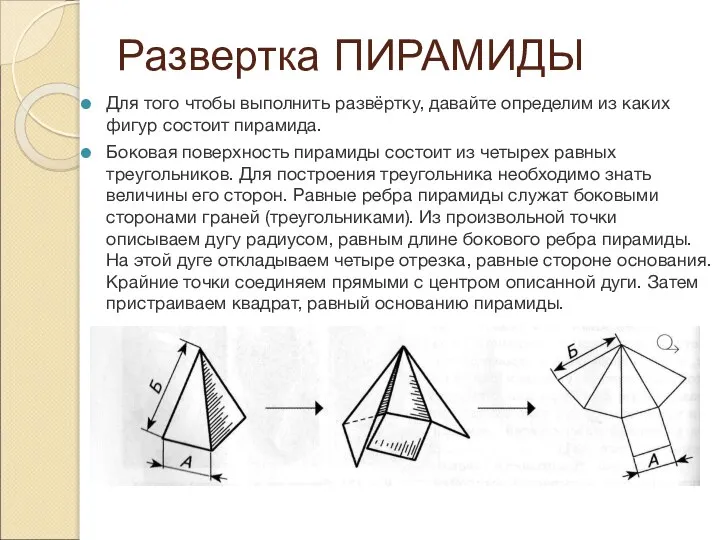
Для того чтобы выполнить развёртку, давайте определим из каких фигур состоит пирамида.
Боковая поверхность пирамиды состоит из четырех равных треугольников. Для построения треугольника необходимо знать величины его сторон. Равные ребра пирамиды служат боковыми сторонами граней (треугольниками). Из про­извольной точки описываем дугу радиусом, равным длине бокового ребра пи­рамиды. На этой дуге откладываем четыре отрезка, равные стороне основания. Крайние точки соединяем прямыми с центром описанной дуги. Затем пристраи­ваем квадрат, равный основанию пирамиды.

Развертка четырехгранной пирамиды

Развертка шестигранной пирамиды

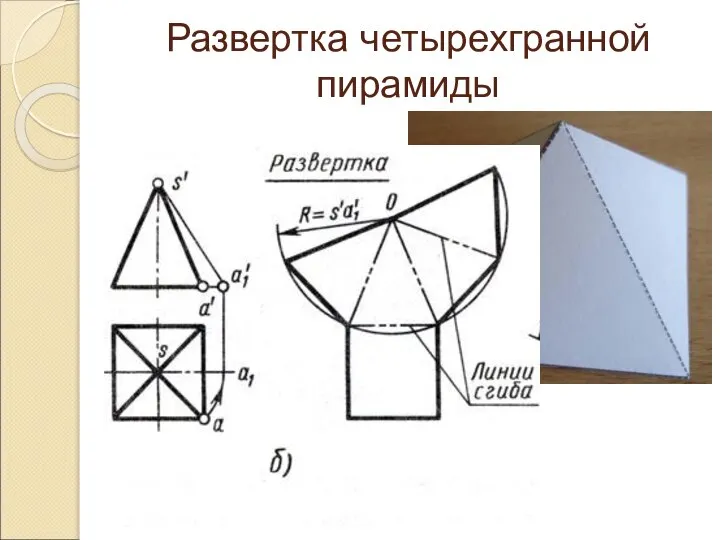
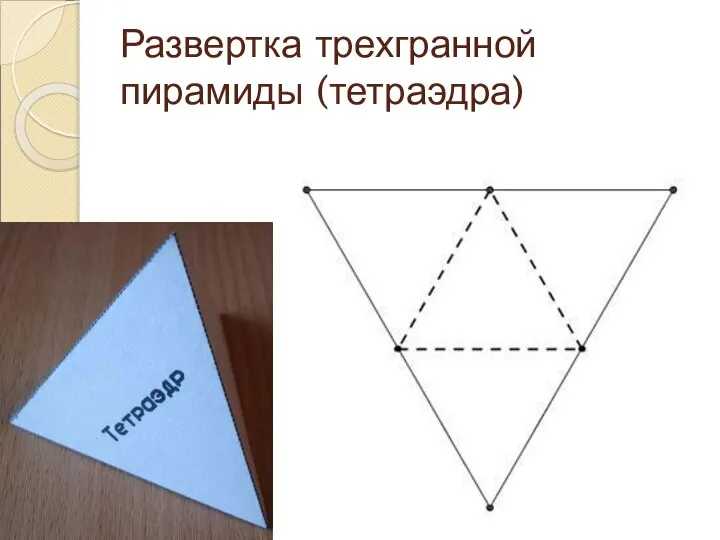
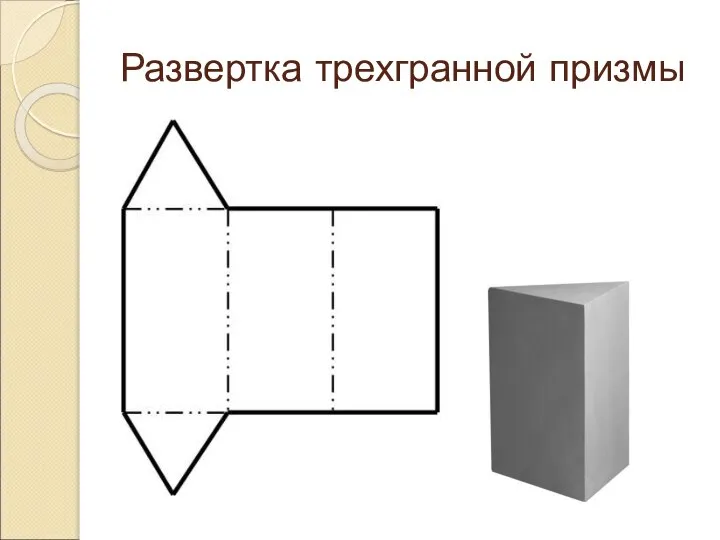
Развертка трехгранной пирамиды (тетраэдра)

Развертка трехгранной призмы

Развертка шестигранной призмы

Развертка пятигранной призмы

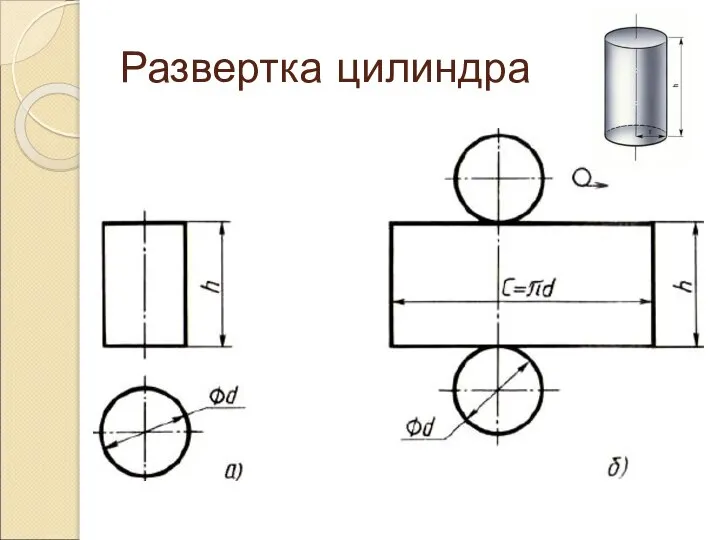
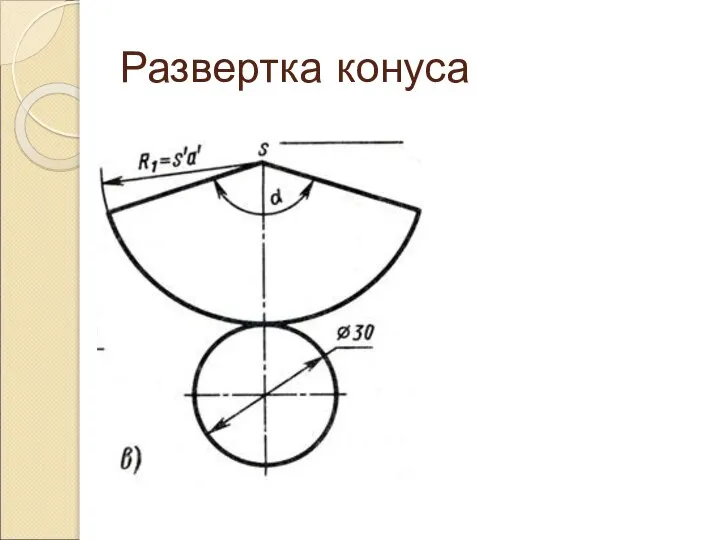
Развертка цилиндра
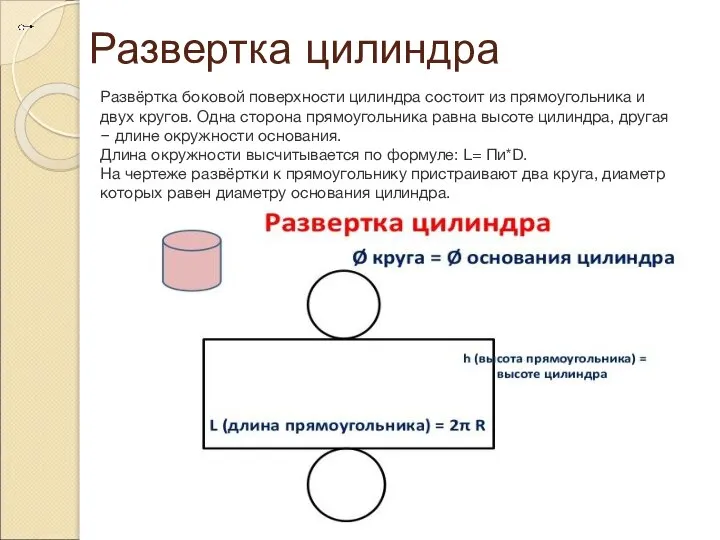
Развёртка боковой поверхности цилиндра состоит из прямоугольника и двух кругов. Одна сторона прямоугольника равна высоте цилиндра, другая – длине окружности основания.
Длина окружности высчитывается по формуле: L= Пи*D.
На чертеже развёртки к прямоугольнику пристраивают два круга, диаметр которых равен диаметру основания цилиндра.

Развертка цилиндра

Развертка конуса

Развертка додекаэдра

Домашнее задание
Изготовить модель геометрического тела высотой не менее 20 см