Вариационный ряд. Группировка данных при качественной и количественной вариациях

ПЛАН:
Вариационный ряд;
Группировка данных при качественной и количественной вариациях;
Мода и медиана.

Вариационный ряд— это статистический ряд распределения значений изучаемого количественного признака, расположенных в порядке убывания или возрастания.
Вариационные ряды бывают (виды):
а) простыми и взвешенными;
б) сгруппированными и несгруппированными;
в) дискретными (прерывными) и непрерывными;9
г) одномодальными и мультимодальными;
д) симметричными и асимметричными;
е) четными и нечетными.
Основные обозначения вариационного ряда:
V — варианта, отдельное числовое выражение изучаемого признака;
р — частота («вес») варианты, число ее повторений в вариационном
ряду;
n — общее число наблюдений (т. е. сумма всех частот, n = ∑ р);
Vmax и Vmin — крайние варианты, ограничивающие вариационный
ряд (лимиты ряда);
А — амплитуда ряда

Назначение вариационного ряда:
вариационный ряд необходим для определения средних величин и критериев разнообразия признака, подлежащих изучению.
Правила составления вариационных рядов:
1) расположить все варианты по порядку;
2) суммировать единицы, имеющие одинаковый признак, т.е. найти частоту каждой варианты;
3) определить количество групп и размер интервала;
4) разбить весь ряд на группы, используя выбранный интервал и строго соблюдая непрерывность сгруппированного ряда;
5) дать графическое изображение.

Группировка данных при качественной вариации.
Чтобы проанализировать ту или иную совокупность, необходимо сгруппировать полученные отдельные варианты, а затем представить группировку в виде таблицы или ряда. Это связано с тем, что при упорядочении полученных данных, легко обработать их математически и вывести показатели, которые будут исчерпывающе характеризовать изучаемую совокупность.
Наиболее простая группировка при качественной вариации. Так если норки отличаются по окраске, то их распределение может быть выражено в количестве животных, и в процентном отношении, которые составляют норки каждой окраски от общего количества животных.

Группировка данных в случае количественного дискретного признака
Для группировки данных в этом случае располагают все варианты в порядке возрастания и указывают частоты , с которыми они встречаются в данной совокупности. Частота п1 варианты х,. показывает, сколько раз варианта встречается в вариационном ряду.
Пример 1. Имеются данные об оценках 24 курсантов, полученных ими на экзамене.
Минимальное значение оценки xmin = 2 , максимальное хтах = 5 .

Дискретный вариационный ряд
Таблица задает дискретный вариационный ряд -последовательность вариант и соответствующих им частот. Отметим, что сумма всех частот вариационного ряда равна объему выборки п.

Графическое изображение дискретного вариационного ряда называется полигоном.
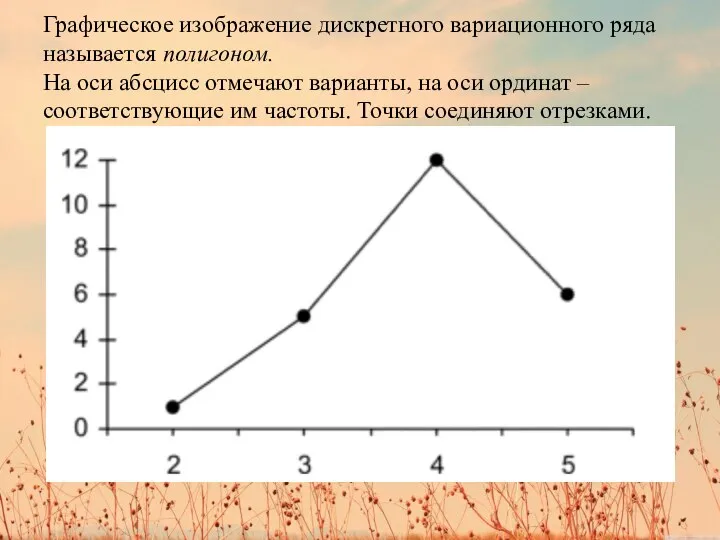
На оси абсцисс отмечают варианты, на оси ординат –
соответствующие им частоты. Точки соединяют отрезками.

МОДА И МЕДИАНА.
Класс, обладающий наибольшей частотой встречаемости называется модальным. Значения модального класса называют модой и обозначается символом Мо. Величина моды является типичной для всей совокупности.
Когда класс охватывает несколько значений вариант, то для его характеристики надо вычислить среднее значение класса или середину класса, что и будет являться значением моды.
Медиана – это значение варианты, находящейся точно в середине ряда, она обозначается Ме. Чтобы найти такую варианту необходимо провести ранжирование вариант от минимальных значений до максимальных.
При нечетном числе вариант, допустим 25, медиане будет соответствовать значение варианты, находящейся точно в середине. В нашем случае 13 варианты.
Чтобы определить медиану при четном числе вариант, надо определить среднее значение двух срединных вариант, что и будет соответствовать медиане.
Например, если число вариант 26, медиана равна значению 13+14 варианты, деленное на два.