Показательное уравнение

Уравнения
равносильно уравнению f(x) = g(x)
1.
2.
Обоснование:
Если степени с равными основаниями, отличными от единицы и большими нуля, равны, то показатели равны;
2) функция монотонна на R, поэтому каждое свое значение
она принимает при единственном значении аргумента.
(уравнивание показателей)

Неравенства
1) Равносильно неравенству f(x) > g(x), а>1
Обоснование:
а) Показательная функция монотонно возрастает (убывает) на R, поэтому большему (меньшему) значению функции соответствует большее значение аргумента.
б) Если a>1, то из неравенства
(сравнение показателей)
2) Равносильно неравенству f(x) < g(x), 0<а<1.
если 0

Решите двойные неравенства:
т.к. показательная функция
с основанием а =5, а>1 возраста-
ет на R, то большему значению
функции соответствует большее
значение аргумента, имеем
Решение.
Ответ: (0;3)
Решение.
т.к. основание степени а = 1/3,
0
Имеем

Функционально-графический метод
решения неравенства f(x) < g(x)
:
1. Подбором найдем корень уравнения f(x)=g(x), используя свойства монотонных функций;
2. Построим схематически графики обеих функций,
проходящие через точку с найденной абсциссой;
3. Выберем решение неравенства, соответствующее
знаку неравенства;
4. Запишем ответ.

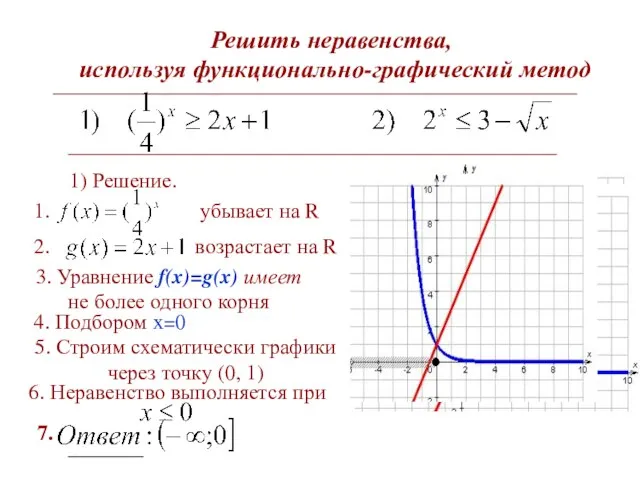
Решить неравенства,
используя функционально-графический метод
1) Решение.
3. Уравнение f(x)=g(x) имеет
не более одного корня
4. Подбором x=0
5. Строим схематически графики
через точку (0, 1)

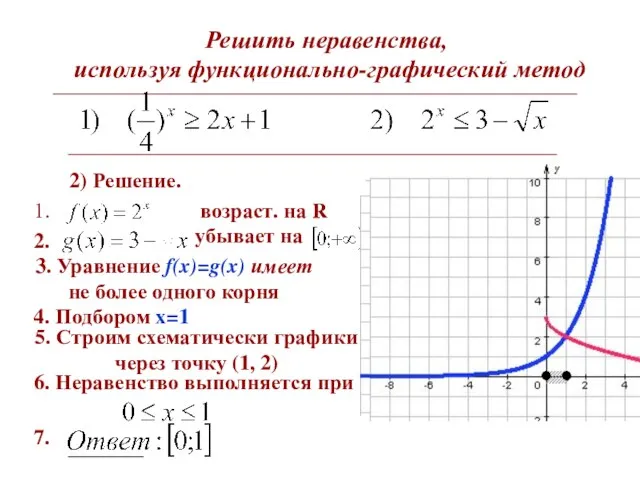
Решить неравенства,
используя функционально-графический метод
2) Решение.
3. Уравнение f(x)=g(x) имеет
не более одного корня
4. Подбором x=1
5. Строим схематически графики
через точку (1, 2)
6. Неравенство выполняется при