Урок-лекция Угол между двумя векторами

План:
Определение скалярного произведения
Скалярное произведение векторов в координатной форме
Нахождение угла между векторами

Определение скалярного произведения
Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними, то есть:
(1)
где

Определение скалярного произведения
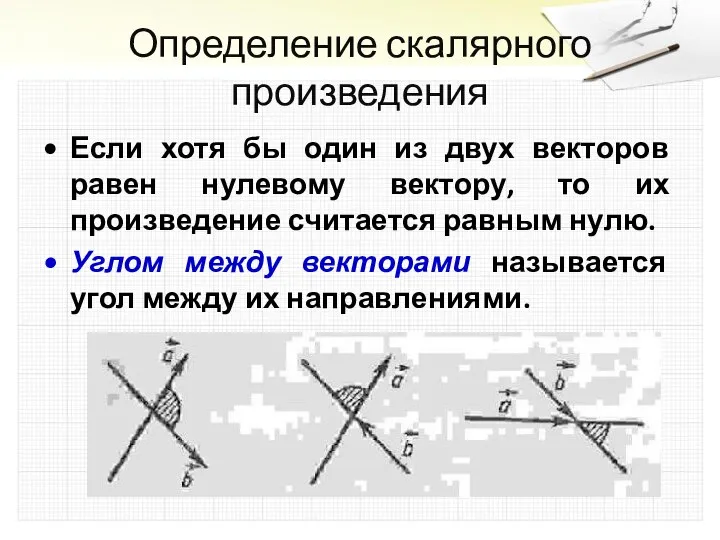
Если хотя бы один из двух векторов равен нулевому вектору, то их произведение считается равным нулю.
Углом между векторами называется угол между их направлениями.

Пример №1
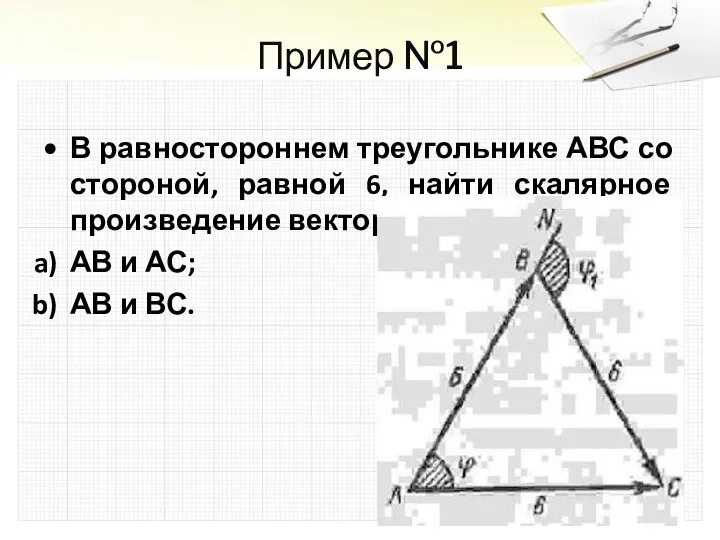
В равностороннем треугольнике АВС со стороной, равной 6, найти скалярное произведение векторов:
АВ и АС;
АВ и ВС.

Решение:
Так как угол ϕ между векторами АВ и АС (и их направлениями) равен 60°, то для скалярного произведения этих векторов получим:

Решение:
Угол ϕ между векторами АВ и ВС (то есть угол между их направлениями) есть угол ϕ1=120°, поэтому:

Скалярное произведение векторов в координатной форме
Пусть два ненулевых вектора заданы своими координатами: , .
Это значит, что векторы a и b разложены в базисе (i;j), то есть ,
Найдём их произведение:
(2)
Так как вектора i и j – единичные и взаимно перпендикулярные, то i²=1; j²=1; ij=0. Подставив эти значения в равенство (2), получим

Скалярное произведение векторов в координатной форме
Так как вектора i и j – единичные и взаимно перпендикулярные, то i²=1; j²=1; ij=0. Подставив эти значения в равенство (2), получим
(3)
Итак, скалярное произведение векторов, заданных своими координатами, равно сумме произведений одноимённых координат.

Пример №2
Найти скалярное произведение векторов a=(3;5) и b=(-2;7).
Решение:
Здесь xa=3; xb=-2; ya=5; yb=7. Используя формулу (3), получим:

Нахождение угла между
векторами
Из определения скалярного произведения двух векторов можно получить формулу:
(4)
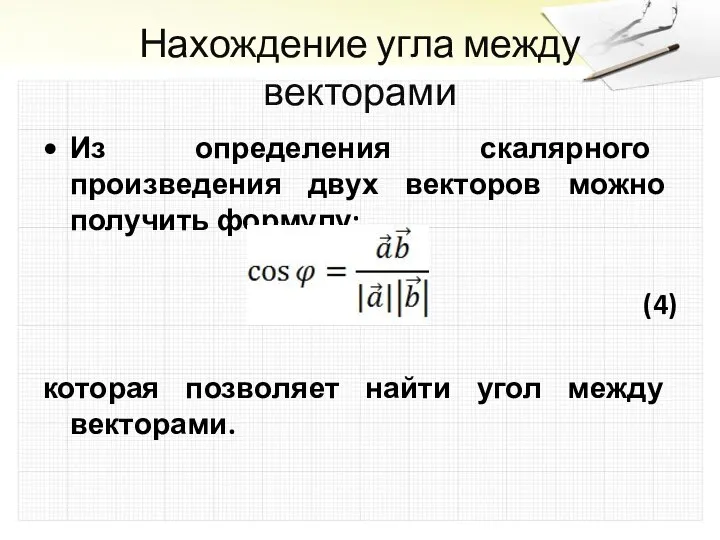
которая позволяет найти угол между векторами.

Нахождение угла между
векторами
Учитывая, что
формулу (4) можно записать в координатной форме:

Пример №3
Найти угол между векторами:
a=(4;0) и b=(2;-2);
a=(5;-3) и b=(3;5).
Используя формулу (5), находим: ,
Решение:

Решение:
Имеем:

Домашнее задание
Лисичкин В. Т., Соловей чик И. Л. Математика в задачах с решениями
№42, 43, 48, 49, 54, 55