Содержание
- 2. Показательное уравнение – это уравнение, в котором неизвестное содержится в показателе степени. Показательное уравнение сводится к
- 3. Пример 1.
- 4. 2. Чтобы привести уравнение к виду (1) необходимо в левой части уравнения вынести за скобки общий
- 5. Пример 2.
- 6. 3. Можно разделить обе части уравнения на выражение, не равное нулю
- 7. Пример 3.
- 8. 4. Некоторые показательные уравнения заменой сводятся к квадратным. Надо помнить, что t>0, так как показательная функция
- 9. Пример 4.
- 10. Алгоритм решения показательных уравнений 1. Уравниваем основания степеней во всех слагаемых, содержащих неизвестное в показателе степени.
- 11. Графическое решение уравнения сводится к построению графиков функций левой и правой частей уравнения, нахождению по рисунку
- 13. Скачать презентацию










 pril
pril Название компонентов и результата деления (2 класс)
Название компонентов и результата деления (2 класс) Параллельность прямых в пространстве
Параллельность прямых в пространстве Тесты по математике
Тесты по математике Презентация на тему Действия с целыми числами
Презентация на тему Действия с целыми числами  Прямоугольник. Ось симметрии
Прямоугольник. Ось симметрии Теорема Пифагора
Теорема Пифагора Оболочки отрицательной Гаусовой кривизны
Оболочки отрицательной Гаусовой кривизны Квадрат. Прямоугольник
Квадрат. Прямоугольник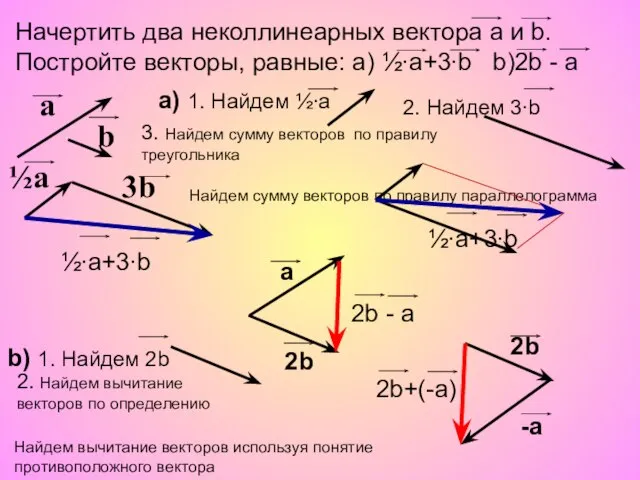 Векторы (9 класс) Задачи
Векторы (9 класс) Задачи Многочлены от одной переменной
Многочлены от одной переменной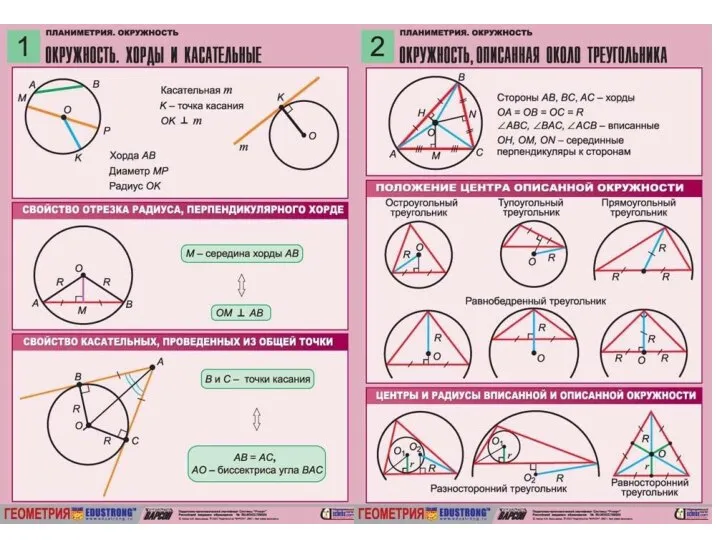 Геометрия. Конспекты
Геометрия. Конспекты Повторение таблицы умножения. Игра хоккей
Повторение таблицы умножения. Игра хоккей Презентация на тему Сложение чисел с разными знаками (6 класс)
Презентация на тему Сложение чисел с разными знаками (6 класс)  Осевая симметрия
Осевая симметрия Вписанная и описанная окружности
Вписанная и описанная окружности Деление на трехзначное число
Деление на трехзначное число Умножение натуральных чисел. Графический диктант. 5 класс
Умножение натуральных чисел. Графический диктант. 5 класс Квадрат
Квадрат Презентация по математике "Решение физических задач графическим способом" -
Презентация по математике "Решение физических задач графическим способом" -  Золотое сечение в природе
Золотое сечение в природе Законы булевой алгебры
Законы булевой алгебры Степень числа с натуральным показателем
Степень числа с натуральным показателем Степенная функция
Степенная функция Презентация на тему Уравнение множественной регрессии
Презентация на тему Уравнение множественной регрессии  Математика. 1 класс
Математика. 1 класс Цифры
Цифры Арккосинус. Решение уравнения cos t = a
Арккосинус. Решение уравнения cos t = a