Векторы (9 класс) Задачи

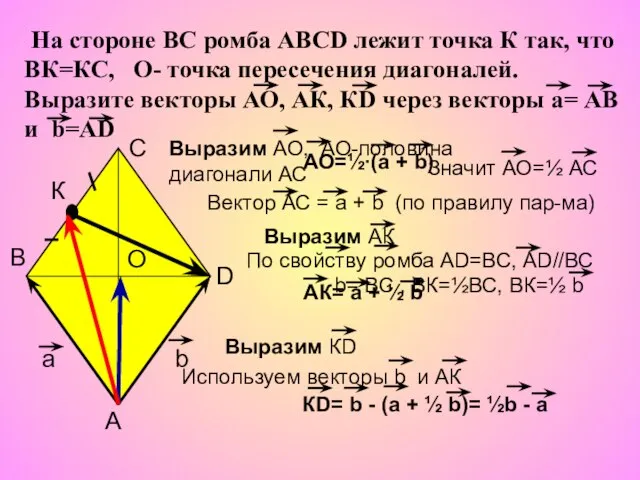
На стороне ВС ромба АВСD лежит точка К так, что ВК=КС, О- точка пересечения диагоналей. Выразите векторы АО, АК, КD через векторы а= АВ и b=АD
В
К
D
С
А
О
b
а
Выразим АО, АО-половина
диагонали АС
Вектор АС = а + b (по правилу пар-ма)
Выразим АК
Значит АО=½ АС
По свойству ромба АD=ВС, АD//ВС
b= ВС , ВК=½ВС, ВК=½ b
АК= а + ½ b
Выразим КD
Используем векторы b и АК
КD= b - (а + ½ b)= ½b - a
АО=½∙(а + b)

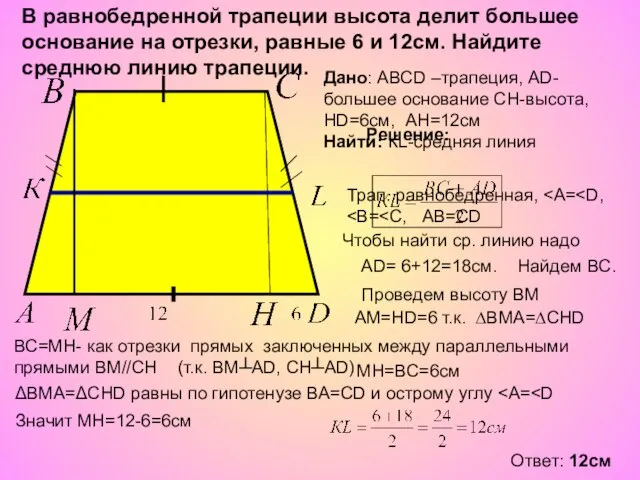
В равнобедренной трапеции высота делит большее основание на отрезки, равные 6 и 12см. Найдите среднюю линию трапеции.
Дано: АВСD –трапеция, АD-большее основание СН-высота, НD=6см, АН=12см
Найти: КL-средняя линия
Трап. равнобедренная, <А=
Чтобы найти ср. линию надо
АD= 6+12=18cм.
ВС=МН- как отрезки прямых заключенных между параллельными прямыми ВМ//CH
Проведем высоту ВМ
(т.к. ВМ┴АD, СН┴АD)
АМ=НD=6 т.к. ∆ВМА=∆СНD
ΔВМА=ΔСНD равны по гипотенузе ВА=СD и острому углу <А=
Значит МН=12-6=6см
МН=ВС=6см
Ответ: 12см
Найдем ВС.
Решение:

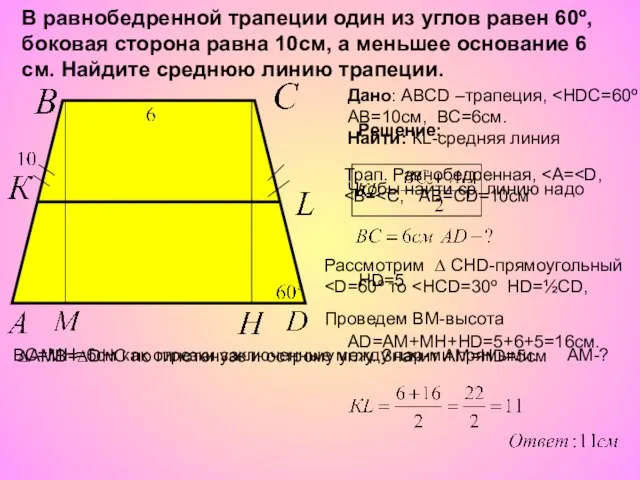
В равнобедренной трапеции один из углов равен 60º, боковая сторона равна 10см, а меньшее основание 6 см. Найдите среднюю линию трапеции.
Дано: АВСD –трапеция, <НDC=60º АВ=10см, ВС=6см.
Найти: КL-средняя линия
Трап. Равнобедренная, <А=
Чтобы найти ср. линию надо
Рассмотрим ∆ СНD-прямоугольный
Проведем ВМ-высота
ВС=МН=6см как отрезки заключенные между пар-ми прямыми. АМ-?
∆АМВ=∆DHC по гипотенузе и острому углу. Значит АМ=НD=5см
AD=АМ+МН+НD=5+6+5=16см.
Решение:
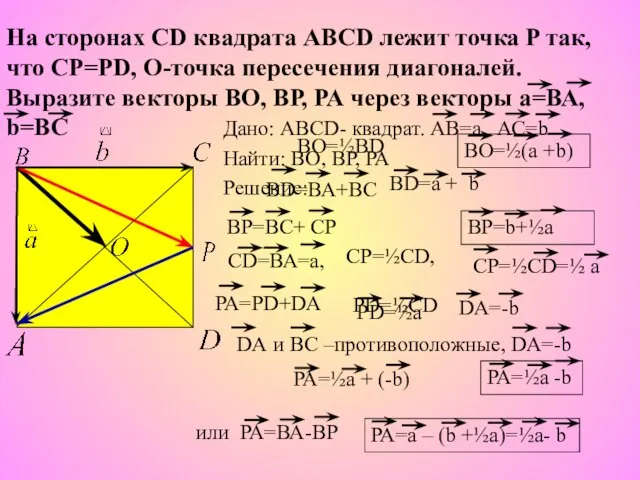
НD=5

Дано: ABCD- квадрат. АВ=а, АС=b
Найти: ВО, ВР, РА
Решение:
На сторонах СD квадрата АВСD лежит точка P так, что СP=PD, О-точка пересечения диагоналей. Выразите векторы ВО, ВР, РА через векторы а=ВА, b=ВС
ВО=½ВD
ВD=ВА+ВС
ВD=а + b
ВО=½(а +b)
СD=ВА=а,
СР=½СD,
СР=½СD=½ a
BР=ВС+ СР
BР=b+½а
РА=РD+DA
РD=½CD
РD=½а
DА и ВС –противоположные, DA=-b
РА=½а + (-b)
РА=½а -b
или РА=ВА-ВР
РА=а – (b +½а)=½а- b
DA=-b

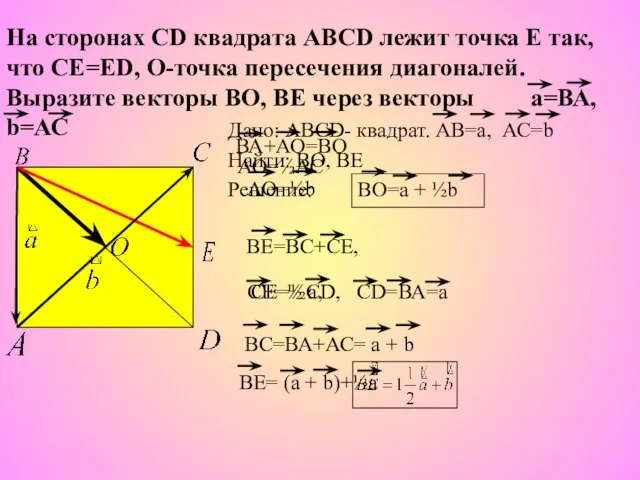
Дано: ABCD- квадрат. АВ=а, АС=b
Найти: ВО, ВЕ
Решение:
На сторонах СD квадрата АВСD лежит точка Е так, что СЕ=ЕD, О-точка пересечения диагоналей. Выразите векторы ВО, ВЕ через векторы а=ВА, b=АС
АО=½АС
АО=½b
ВА+АО=ВО
ВО=а + ½b
СЕ=½СD, СD=ВА=а
СЕ=½ a,
ВЕ=ВС+СЕ,
ВЕ= (а + b)+½а
ВС=ВА+АС= а + b