Полуплоскость и угол

Угол
его стороны вместе составляют одну прямую.
одна сторона у них общая, а две другие …
вместе составляют одну прямую.
стороны одного угла дополняют до прямых стороны другого угла.
одной из частей плоскости, ограниченной этими лучами.
Общая вершина называется…
вершиной угла.
Сами лучи называются…
сторонами угла.
двумя лучами с общей вершиной и …

Равенство углов
Одной из основных операций, которую можно производить с углами, является операция откладывания данного угла в ту или другую сторону от данного луча. Получающийся при этом угол называется равным исходному углу.
В качестве аксиом принимаются следующие свойства.
От любого луча на плоскости в заданную сторону можно отложить только один угол, равный данному.
Все развернутые углы равны.

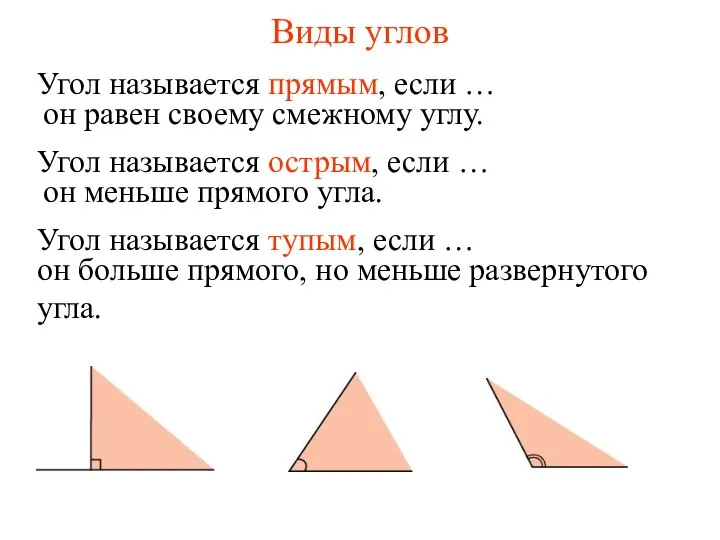
Виды углов
он равен своему смежному углу.
он меньше прямого угла.
он больше прямого, но меньше развернутого угла.

Сложение углов
Аналогичным образом поступают для вычитания из большего угла меньшего.
Чтобы сложить два угла, например АОВ и CО1D, отложим угол CO1D от луча ОВ так, чтобы точки A и D находились по разные стороны от прямой ОВ. Обозначим ОЕ луч, в который перейдет луч О1D. Тогда угол АОЕ даст сумму углов АОВ и CО1D.

Вопрос 1
Ответ: На две части.
На сколько частей прямая разбивает плоскость?

Вопрос 2
Ответ: а) Если отрезок, соединяющий эти точки, пересекается с прямой.
В каком случае две точки принадлежат:
а) одной полуплоскости;
б) разным полуплоскостям относительно данной прямой?
б) если отрезок, соединяющий эти точки, не пересекается с прямой.

Вопрос 3
Какая фигура называется углом? Что называется вершиной угла? Что называется сторонами угла?
Ответ: Фигура, образованная двумя лучами с общей вершиной и одной из частей плоскости, ограниченной этими лучами, называется углом. Общая вершина называется вершиной угла, а сами лучи - сторонами угла.

Вопрос 4
Какой угол называется развернутым?
Ответ: Угол называется развернутым, если его стороны вместе составляют прямую.

Вопрос 5
Какие углы называются смежными?
Ответ: Два угла называются смежными, если одна сторона у них общая, а две другие составляют вместе прямую.

Вопрос 6
Какие углы называются вертикальными?
Ответ: Два угла называются вертикальными, если стороны одного угла дополняют до прямых стороны другого угла.

Вопрос 7
Как обозначаются углы?

Вопрос 8
Какие два угла называются равными?
Ответ: Два угла называются равными, если один получается из другого операцией откладывания угла.

Вопрос 9
Как сложить два угла?
Ответ: Чтобы сложить два угла, например АОВ и CО1D, отложим угол CO1D от луча ОВ так, чтобы точки A и D находились по разные стороны от прямой ОВ. Обозначим ОЕ луч, в который перейдет луч О1D. Тогда угол АОЕ даст сумму углов АОВ и CО1D.

Вопрос 10
Как обозначается сумма углов AOB и CQD?

Вопрос 11
В каком случае говорят, что угол АOВ меньше угла А1O1В1?
Ответ: Если при откладывании угла АOВ от луча O1В1 луч OВ переходит в луч O1B', лежащий между лучами O1А1 и O1В1, то говорят, что угол АOВ меньше угла А1O1В1.

Вопрос 12
Как обозначается то, что угол AOB меньше угла CQD?

Вопрос 13
Как из большего угла вычесть меньший?
Ответ: Чтобы из большего угла CQD вычесть меньший угол AOB, от луча QC отложим угол CQB’, равный углу AOB. Угол B’QD будет разностью отрезков СQD и AOB.

Вопрос 14
Ответ: а) Угол, равный своему смежному, называется прямым.
Какой угол называется: а) прямым; б) острым; в) тупым?
б) угол, меньший прямого угла, называется острым.
в) угол, больший прямого угла, но меньший развернутого угла, называется тупым.

Вопрос 15
Ответ: Углом между пересекающимися прямыми называется наименьший из углов, образованных лучами, на которые делятся данные прямые точкой их пересечения.
Что называется углом между пересекающимися прямыми?

Вопрос 16
Ответ: Две прямые называются перпендикулярными, если они образуют прямые углы.
Какие прямые называются перпендикулярными?

Вопрос 17
Ответ: Биссектрисой угла называется внутренний луч, делящий этот угол на два равных угла
Что называется биссектрисой угла?

Упражнение 1
На сколько частей могут разбивать плоскость две прямые?

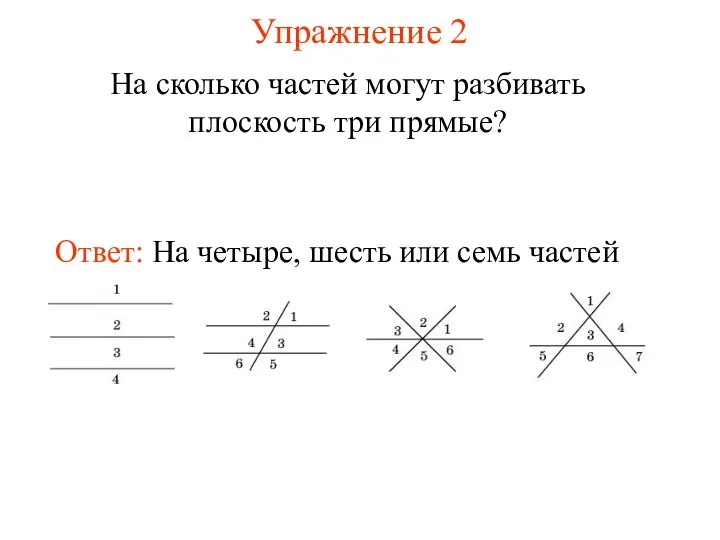
Упражнение 2
На сколько частей могут разбивать плоскость три прямые?

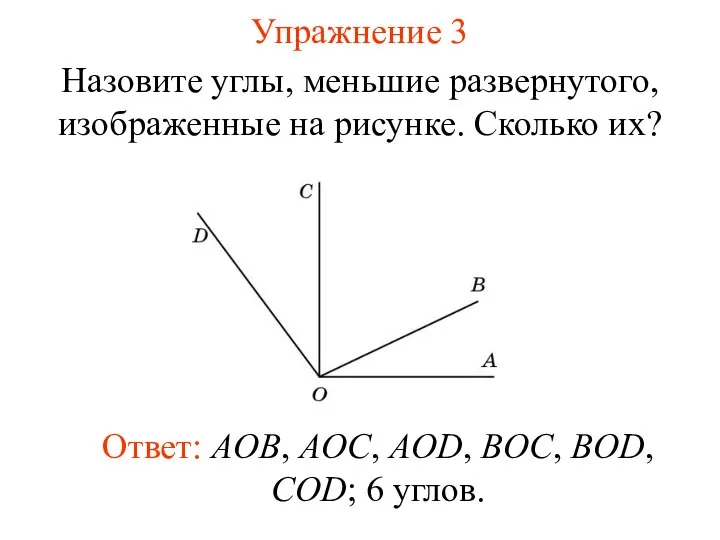
Упражнение 3
Назовите углы, меньшие развернутого, изображенные на рисунке. Сколько их?
Ответ: AOB, AOC, AOD, BOC, BOD, COD; 6 углов.

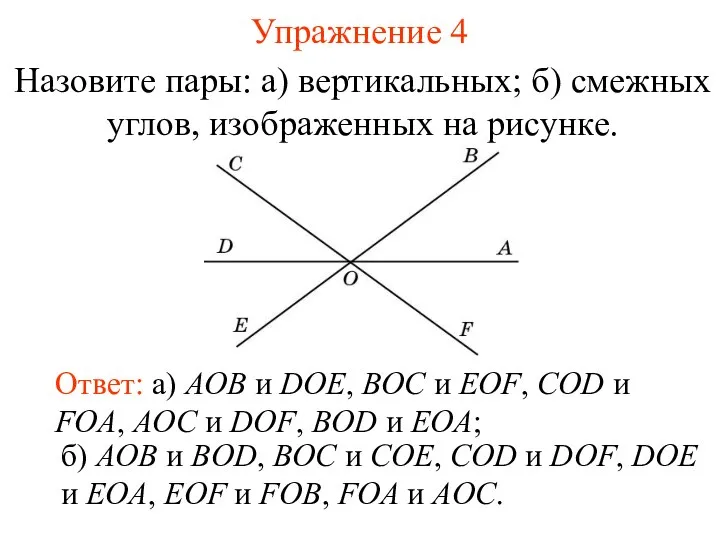
Упражнение 4
Назовите пары: а) вертикальных; б) смежных углов, изображенных на рисунке.
Ответ: а) AOB и DOE, BOC и EOF, COD и FOA, AOC и DOF, BOD и EOA;
б) AOB и BOD, BOC и COE, COD и DOF, DOE и EOA, EOF и FOB, FOA и AOC.

Упражнение 5
Сколько имеется углов, смежных данному углу?
Ответ: Два.

Упражнение 6
Ответ: а) Нет.
Могут ли два смежных угла быть одновременно: а) острыми; б) прямыми; в) тупыми?
б) да.
в) нет.

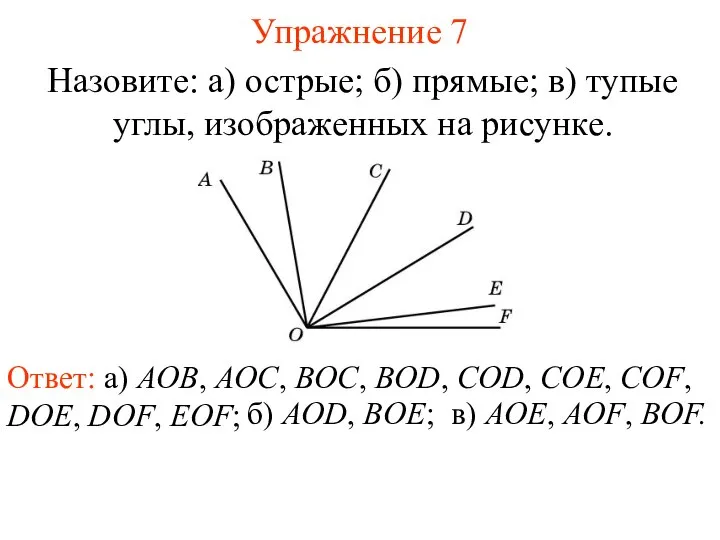
Упражнение 7
Назовите: а) острые; б) прямые; в) тупые углы, изображенных на рисунке.
Ответ: а) AOB, AOC, BOC, BOD, COD, COE, COF, DOE, DOF, EOF;
б) AOD, BOE;
в) AOE, AOF, BOF.

Упражнение 8
Внутри угла проведено: а) 2 луча; б) 3 луча; *в) n лучей, каждый из которых имеет начало в вершине угла. Сколько при этом образуется углов (вместе с данным)?
Ответ: а) 6;
б) 15;

Упражнение 9
Какой угол образуют биссектрисы смежных углов?
Ответ: Прямой.

Упражнение 10
Какой угол образуют биссектрисы вертикальных углов?
Ответ: Развернутый

Упражнение 11
Когда часовая и минутная стрелки часов образуют прямой угол?
Ответ: В 3 ч и 9 ч.