Содержание
- 2. «График – это говорящая линия, которая может о многом рассказать» М.Б. Балк – это море, скрывающее
- 3. n= -1 Выбери показатель степени функции у=хn n=0 n=4 n=3 n=1 n=2
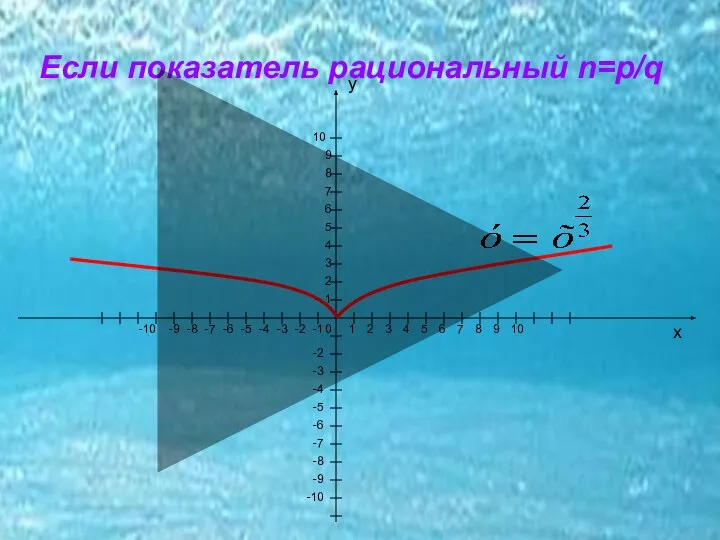
- 4. Степенной функцией называется функция вида у=хn ,где х-независимая переменная, а n- любое действительное число, называемое показателем
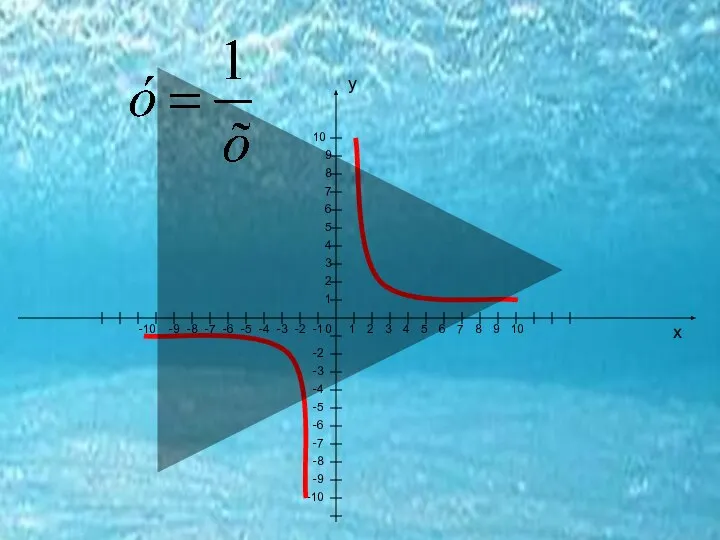
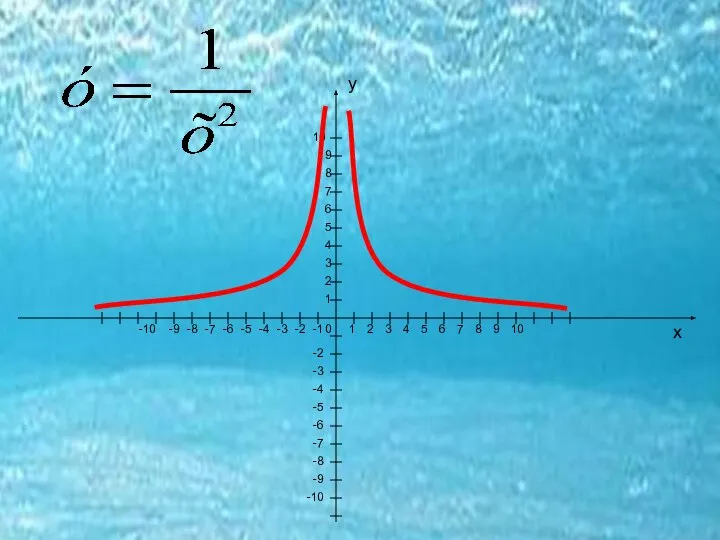
- 5. Добро пожаловать в мир гипербол Гипербола – что это?
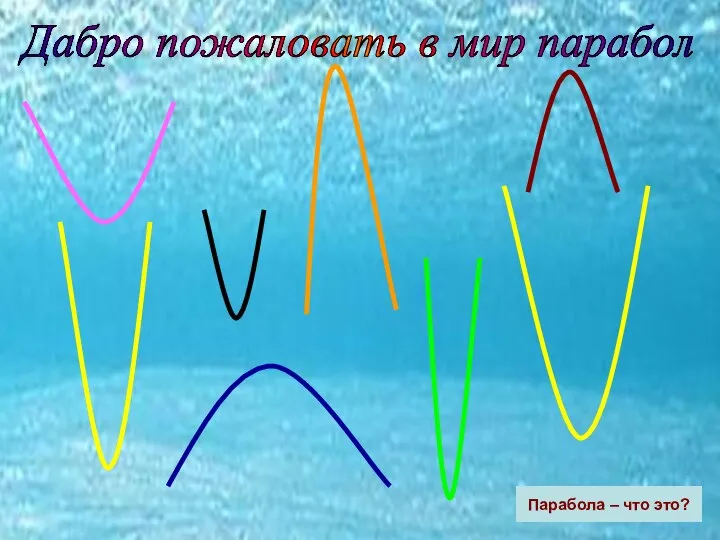
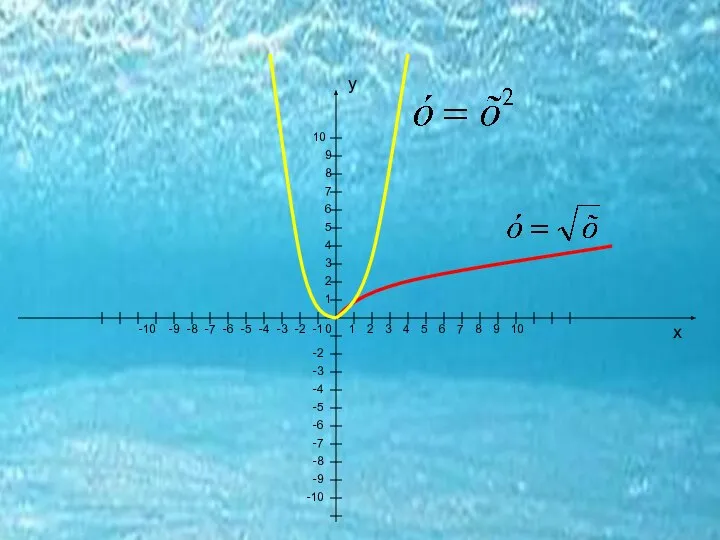
- 6. Дабро пожаловать в мир парабол Парабола – что это?
- 7. Слово «парабола» применяют часто ко всем кривым, уравнение которых являются степенной функцией. ... и это параболы
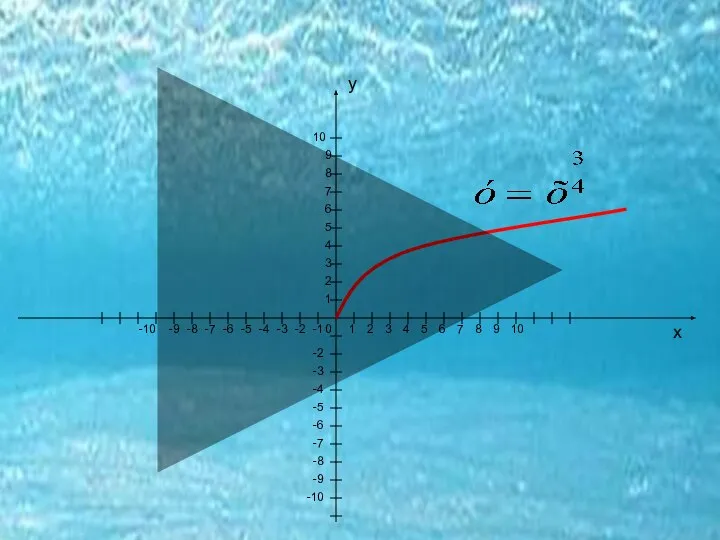
- 8. ... а эти линии состоят из "ветвей" параболы что это?
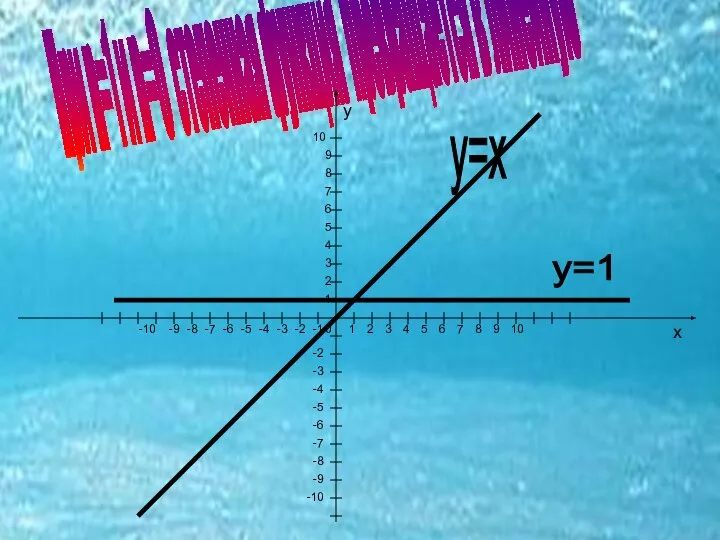
- 9. При n=1 и n=0 степенная функция превращается в линейную 0 х у 2 3 1 4
- 10. Гипербола и парабола – это кривые, получающиеся при сечении кругового конуса (точнее – конической поверхности) плоскостью,
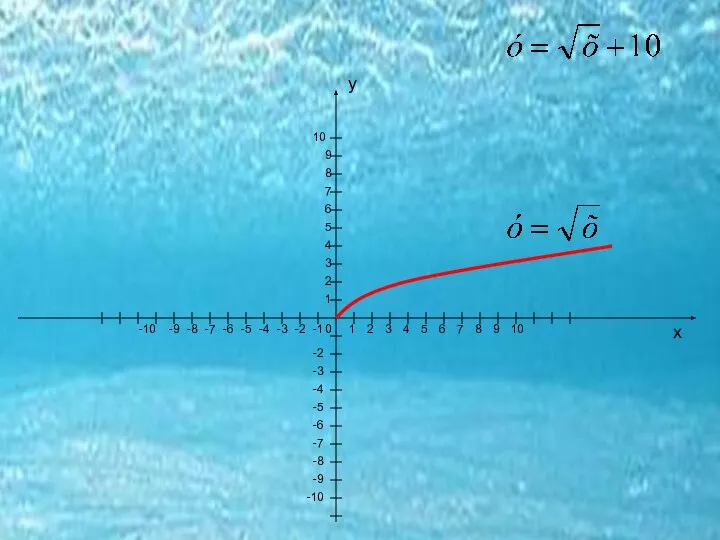
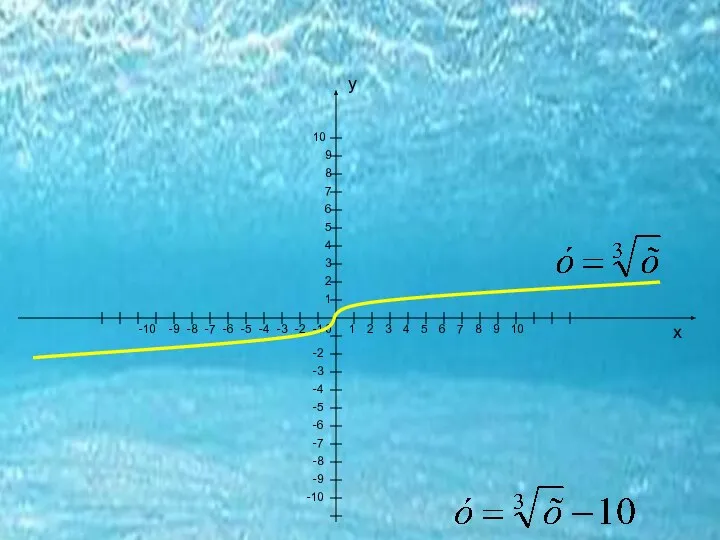
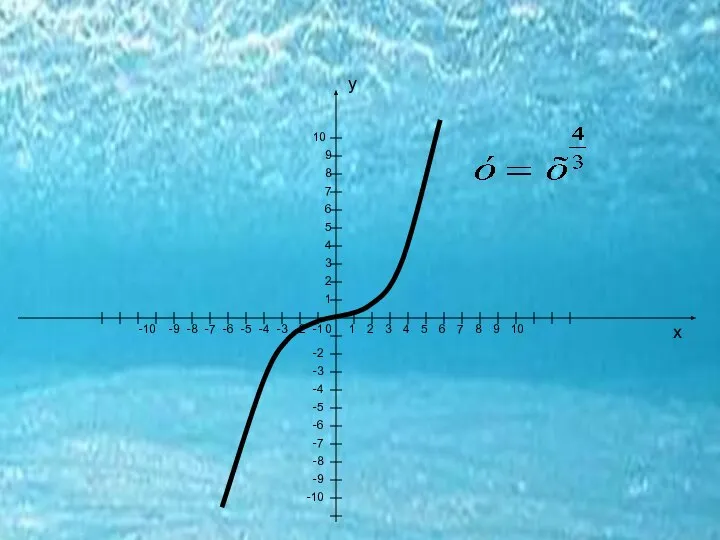
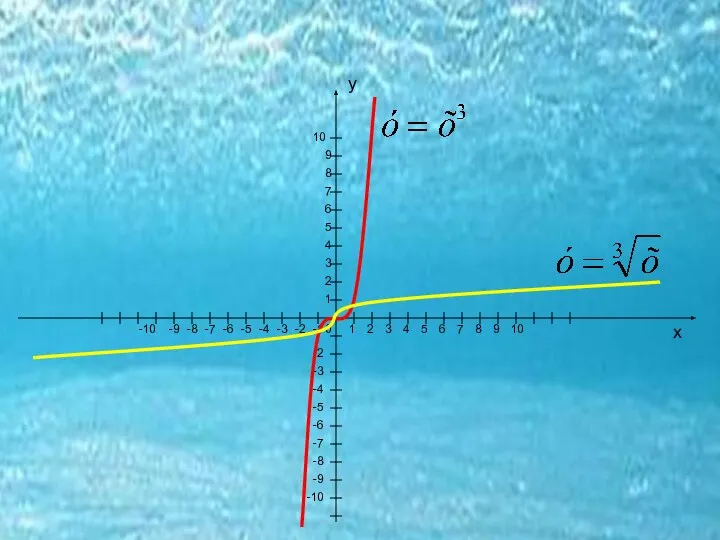
- 11. Все графики функции у=хn весьма дисциплинированы, и действуют только по законам. Каждый график соблюдает свои права
- 12. Все графики функции у=хn весьма дисциплинированы, и действуют только по законам. Каждый график соблюдает свои права
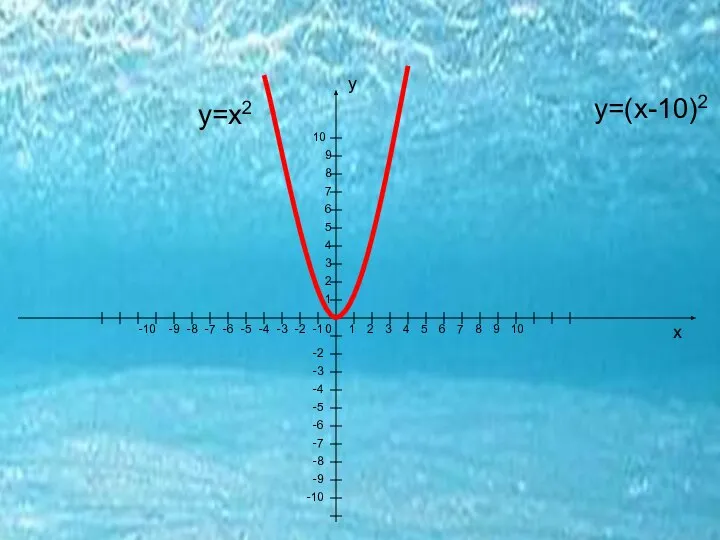
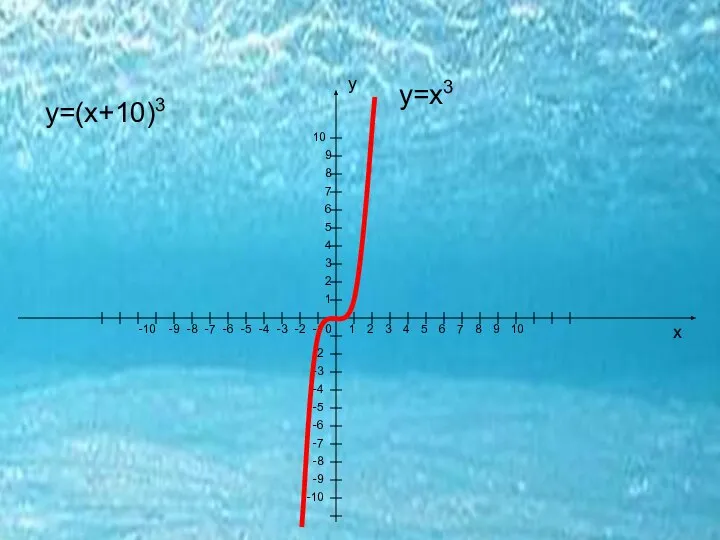
- 14. 3) При движении функции у=хn влево, надо к аргументу х прибавить число в>0. 4) При движении
- 15. Все графики функции у=хn весьма дисциплинированы, и действуют только по законам. Каждый график соблюдает свои права
- 16. Все графики функции у=хn весьма дисциплинированы, и действуют только по законам. Каждый график соблюдает свои права
- 17. Все графики функции у=хn весьма дисциплинированы, и действуют только по законам. Каждый график соблюдает свои права
- 18. 0 х у 2 3 1 4 6 5 7 1 2 3 4 5 6
- 19. 0 х у 2 3 1 4 6 5 7 1 2 3 4 5 6
- 20. 0 х у 2 3 1 4 6 5 7 1 2 3 4 5 6
- 21. 0 х у 2 3 1 4 6 5 7 1 2 3 4 5 6
- 22. 0 х у 2 3 1 4 6 5 7 1 2 3 4 5 6
- 24. 0 х у 2 3 1 4 6 5 7 1 2 3 4 5 6
- 25. 0 х у 2 3 1 4 6 5 7 1 2 3 4 5 6
- 26. 0 х у 2 3 1 4 6 5 7 1 2 3 4 5 6
- 27. 0 х у 2 3 1 4 6 5 7 1 2 3 4 5 6
- 28. 0 х у 2 3 1 4 6 5 7 1 2 3 4 5 6
- 29. 0 х у 2 3 1 4 6 5 7 1 2 3 4 5 6
- 31. Скачать презентацию















 Алгебраические определения
Алгебраические определения Презентация на тему Понятие площади фигуры и ее измерение
Презентация на тему Понятие площади фигуры и ее измерение  Построение треугольника с помощью циркуля и транспортира
Построение треугольника с помощью циркуля и транспортира Решение тестовых задач. Готовимся к ЕГЭ
Решение тестовых задач. Готовимся к ЕГЭ Угол между плоскостями
Угол между плоскостями Презентация на тему Умножение одночленов. Возведение одночленов в степень
Презентация на тему Умножение одночленов. Возведение одночленов в степень  Преобразование выражений, содержащих степени с целым показателем
Преобразование выражений, содержащих степени с целым показателем TOChEChNAYa_I_INTERVAL_NAYa_OTsENKA_SLUChAJNOJ_VELIChINY (1)
TOChEChNAYa_I_INTERVAL_NAYa_OTsENKA_SLUChAJNOJ_VELIChINY (1) Применение теории паркета для доказательства свойств и признаков параллелограмма и трапеции
Применение теории паркета для доказательства свойств и признаков параллелограмма и трапеции Понятие Марковского случайного процесса
Понятие Марковского случайного процесса Действия с рациональными числами
Действия с рациональными числами Правильные многоугольники
Правильные многоугольники Построение графиков тригонометрических функций
Построение графиков тригонометрических функций Спасатели. Игра
Спасатели. Игра Прямой счет, обратный счет. Повторение
Прямой счет, обратный счет. Повторение Фигуры на клетчатой бумаге
Фигуры на клетчатой бумаге Дифференциальные и разностные уравнения
Дифференциальные и разностные уравнения Оригами в математике
Оригами в математике Таблицы. Алгебра 7 класс
Таблицы. Алгебра 7 класс Арифметика в позиционных системах счисления
Арифметика в позиционных системах счисления Геометрический и физический смысл производной. Решение задач
Геометрический и физический смысл производной. Решение задач Неравенства. Решение линейных неравенств
Неравенства. Решение линейных неравенств Сдвиг графика функции у = ах² вдоль осей координат
Сдвиг графика функции у = ах² вдоль осей координат Тригонометрические функции, их графики и свойства
Тригонометрические функции, их графики и свойства Геометрическая мозаика из правильных одноимённых многоугольников
Геометрическая мозаика из правильных одноимённых многоугольников Векторы. Сложение и вычитание векторов
Векторы. Сложение и вычитание векторов Многогранники
Многогранники Координатная плоскость
Координатная плоскость