Содержание
- 2. Число А называется пределом функции у=f(x), при х стремящемся к бесконечности, если для любого, сколь угодно
- 3. При достаточно больших по модулю значениях х, значения функции f(x) очень мало отличаются от числа А
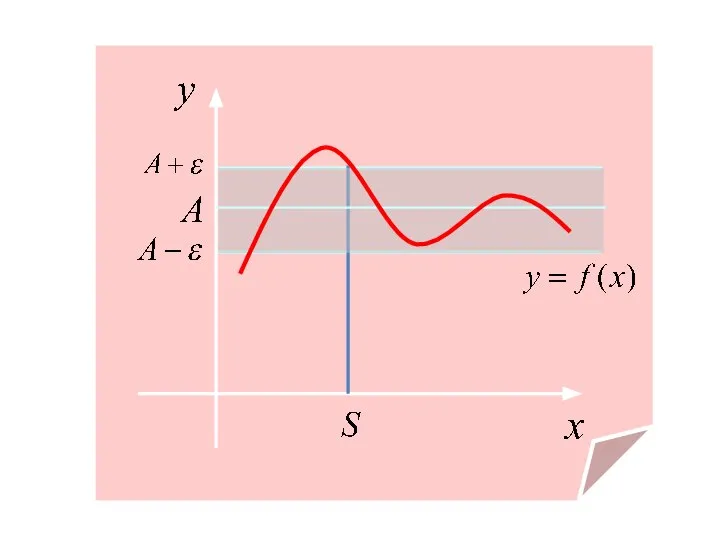
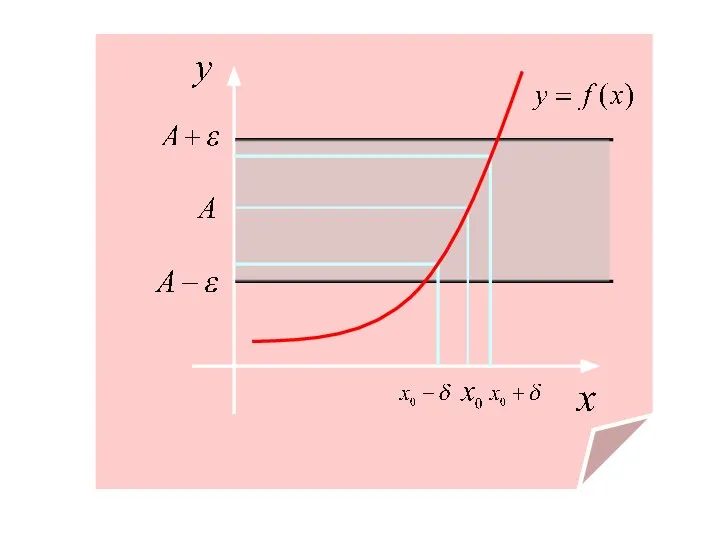
- 4. Рассмотрим геометрический смысл этого определения. Неравенство равносильно двойному неравенству что соответствует расположению части графика у=f(x) в
- 6. Т.е. число А есть предел функции какой бы узкой она не была. если для любого, сколь
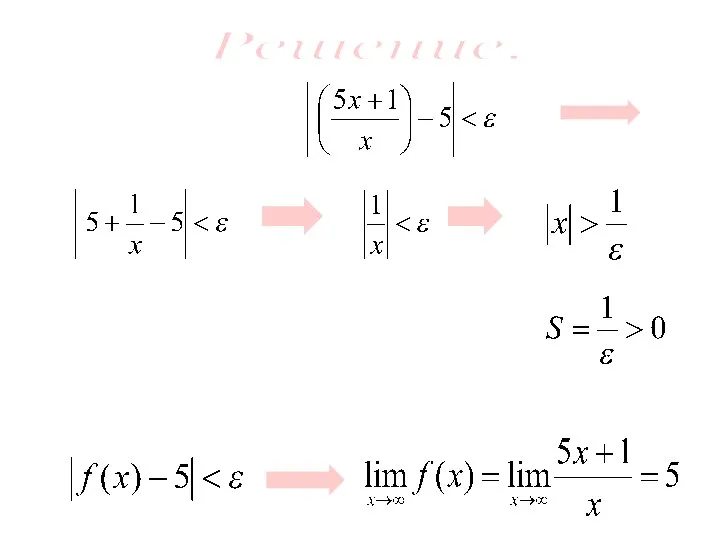
- 7. Доказать, что Пример.
- 8. Т.е. для любого ε >0 существует число Такое, что для всех х, таких что |x|>S, выполняется
- 9. Рассмотренное определение предела при x стремящемся к бесконечности предполагает неограниченное возрастание x по абсолютной величине. Можно
- 10. В случае, когда неравенство должно выполняться при всех x таких, что х>s. В случае, когда неравенство
- 11. Число А называется пределом функции у=f(x), при х→x0, (или в точке x0) если для любого, сколь
- 12. При всех значениях х, достаточно близких к x0, значения функции у=f(x) очень мало отличаются по абсолютной
- 13. Неравенство равносильно двойному неравенству Аналогично неравенство равносильно неравенству Это соответствует расположению части графика в полосе шириной
- 14. Т.е. число А есть предел функции при х→x0, если для любого, сколь угодно малого числа какой
- 16. Доказать, что Пример.
- 17. Пусть ε=0.1 Тогда неравенство будет выполняться при Аналогично, при ε=0.01 Неравенство будет выполняться при Решение.
- 18. Т.е. для любого ε >0 неравенство выполняется при Т.е. для любого ε >0 существует число что
- 19. Определение предела не требует существования функции в самой точке x0, т.к. рассматриваются значения функции в некоторой
- 20. переменная x принимает значения только меньше x0 или, наоборот, больше x0, и при этом функция f(x)
- 21. Определение этих пределов будет аналогично рассмотренному выше при Вместо значений x, удовлетворяющих условию рассматриваются такие x,
- 22. Если пределы функции f(x) слева и справа одинаковы и равны А, то существует общий предел этой
- 24. БЕСКОНЕЧНО МАЛЫЕ ВЕЛИЧИНЫ Функция f(x) называется бесконечно малой величиной, если при или при ее предел равен
- 25. Функция является бесконечно малой величиной при поскольку ПРИМЕР.
- 26. Если функция f(x) имеет при или при предел, равный А, то ее можно представить в виде
- 27. Верна и обратная Если функцию f(x) можно представить как сумму числа А и бесконечно малой величины
- 28. Свойства бесконечно малых величин 1 Алгебраическая сумма бесконечно малых величин есть величина бесконечно малая.
- 29. 2 Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая. 3 Частное от деления
- 30. Пусть являются бесконечно малыми величинами при поскольку ПРИМЕР. Функция
- 31. является ограниченной на любом промежутке, поскольку Функция имеет предел при Тогда функции
- 32. являются бесконечно малыми величинами при
- 33. Замечание Предел отношения двух бесконечно малых величин может быть равен нулю, тогда α(х) называется бесконечно малой
- 34. БЕСКОНЕЧНО БОЛЬШИЕ ВЕЛИЧИНЫ Функция f(x) называется бесконечно большой величиной, если для любого, даже сколь угодно большого
- 35. Если то Если то
- 36. Функция является бесконечно большой величиной при поскольку ПРИМЕР.
- 37. Замечание Бесконечно большая величина является неограниченной функцией при или при но в то же время неограниченная
- 38. Функция является неограниченной функцией, но при она не будет бесконечно большой, поскольку ее значения колеблются, переходя
- 39. Свойства бесконечно больших величин 1 Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.
- 40. 2 Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.
- 41. является бесконечно большой при Функция ПРИМЕР. Функция имеет предел при
- 42. Функция является ограниченной. Тогда функции являются бесконечно большими величинами при
- 43. ТЕОРЕМЫ О ПРЕДЕЛАХ Пусть f(x) и φ(x) – функции, для которых существуют пределы при Тогда справедливы
- 44. ТЕОРЕМА 1. Функция не может иметь более одного предела.
- 45. ТЕОРЕМА 2. Предел алгебраической суммы (разности) конечного числа функций равен сумме (разности) пределов этих функций:
- 46. ТЕОРЕМА 3. Предел произведения конечного числа функций равен произведению пределов этих функций:
- 47. Следствие.
- 48. ТЕОРЕМА 4. Предел частного двух функций равен частному пределов этих функций:
- 49. ТЕОРЕМА 5. Если и то предел сложной функции существует и равен
- 50. Замечание В этих теоремах полагается, что существуют пределы функций f(x) и φ(x), из чего следует существование
- 51. Пример. Но: - не существует
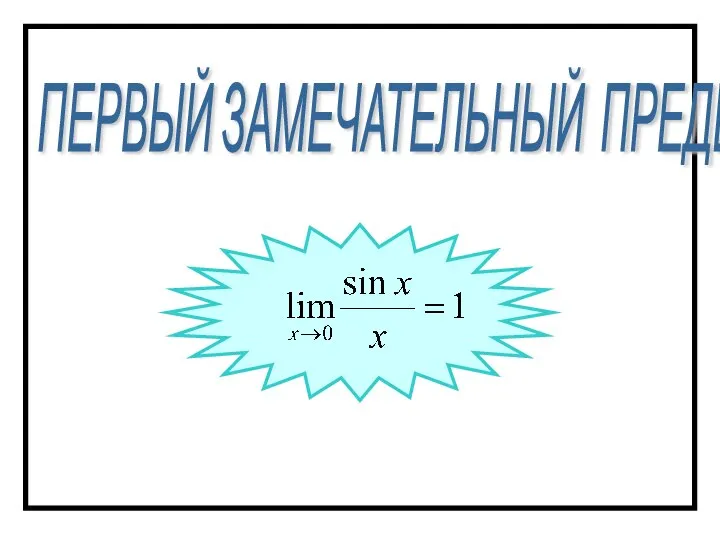
- 52. ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
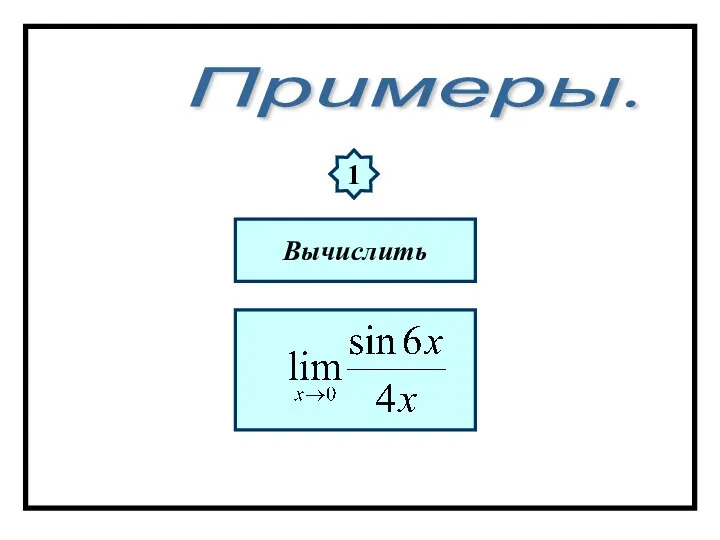
- 53. Примеры. 1 Вычислить
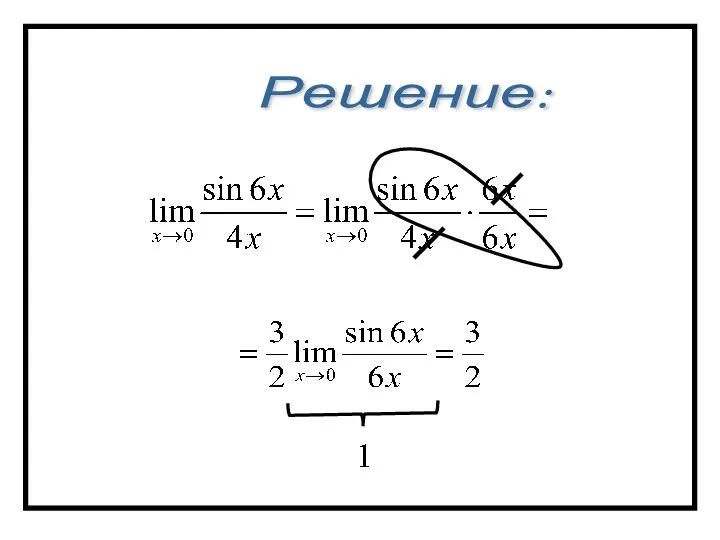
- 54. Решение:
- 55. 2 Вычислить
- 56. Решение:
- 57. Второй замечательный предел
- 58. Пусть , тогда Второй замечательный предел
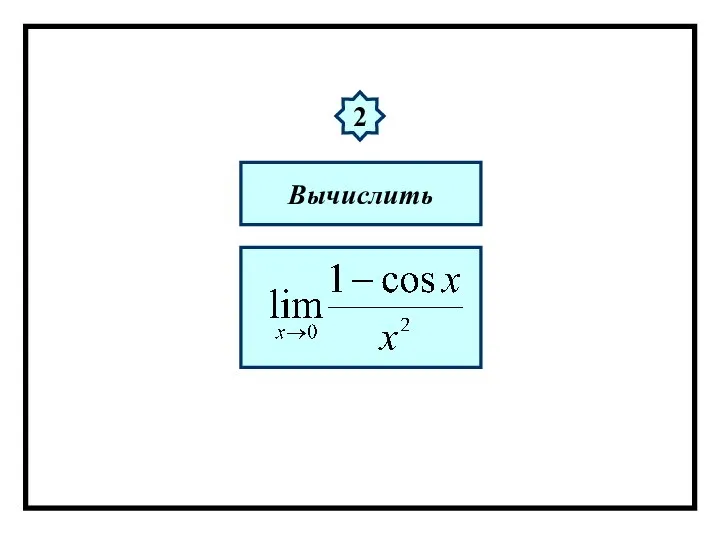
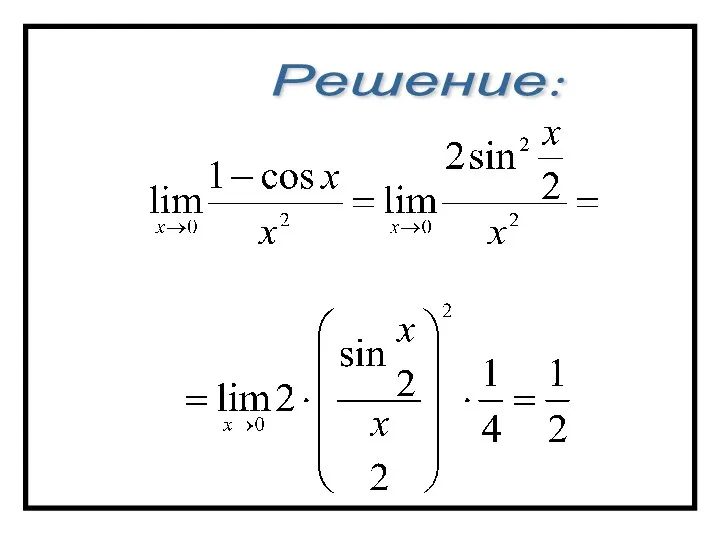
- 59. Примеры. 1 Вычислить
- 60. Решение:
- 61. 2 Вычислить
- 63. Скачать презентацию


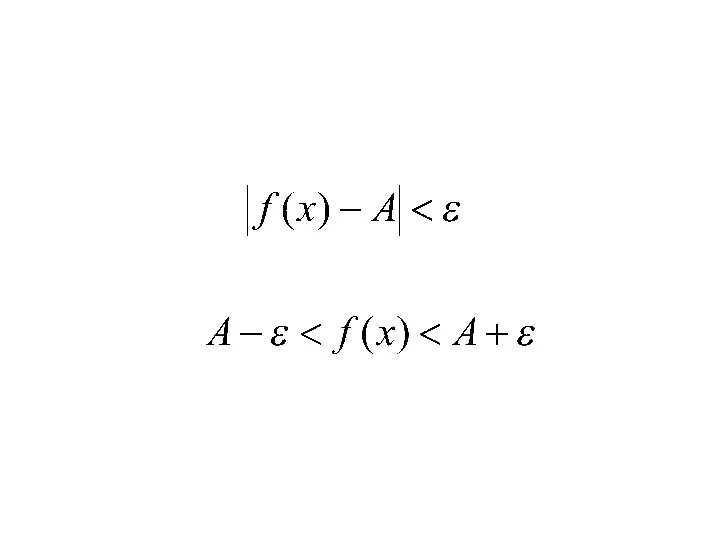
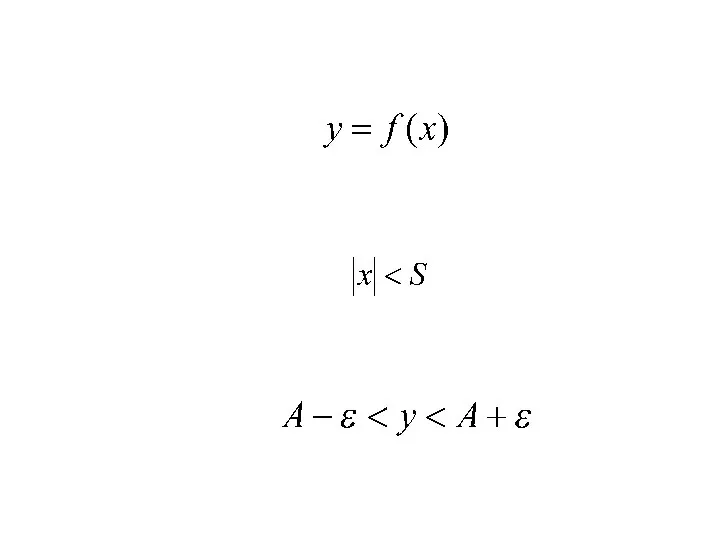


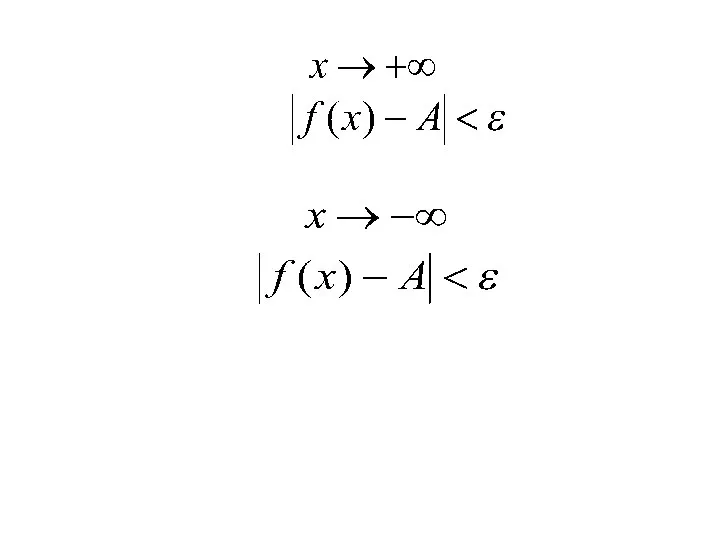


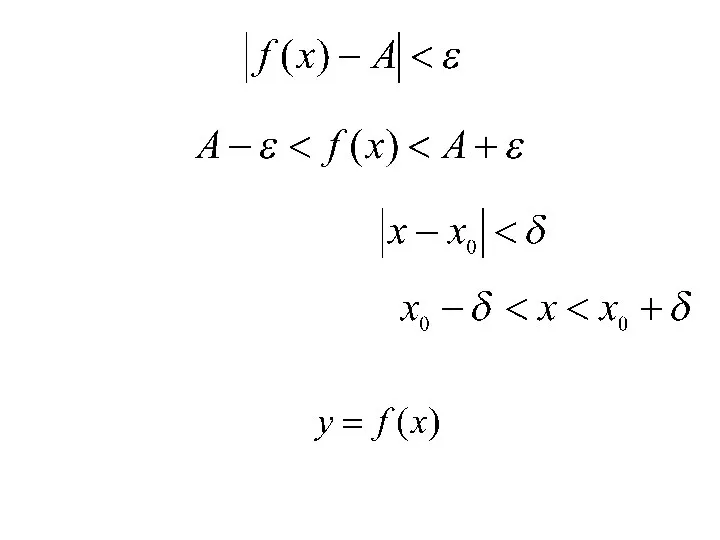

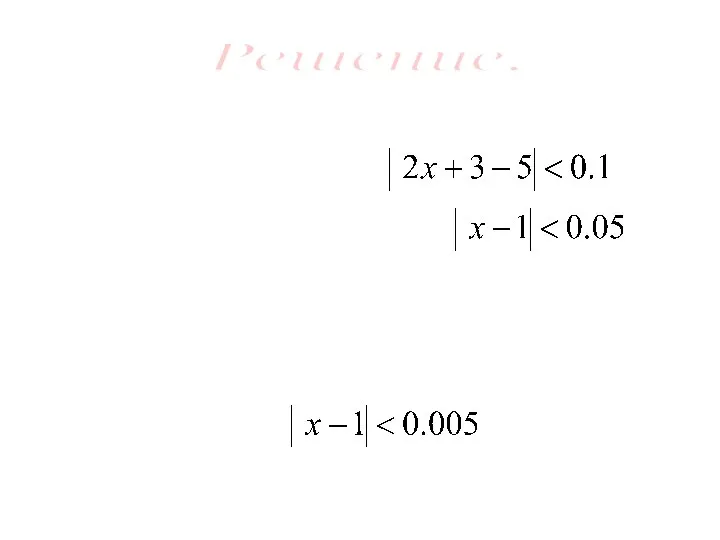
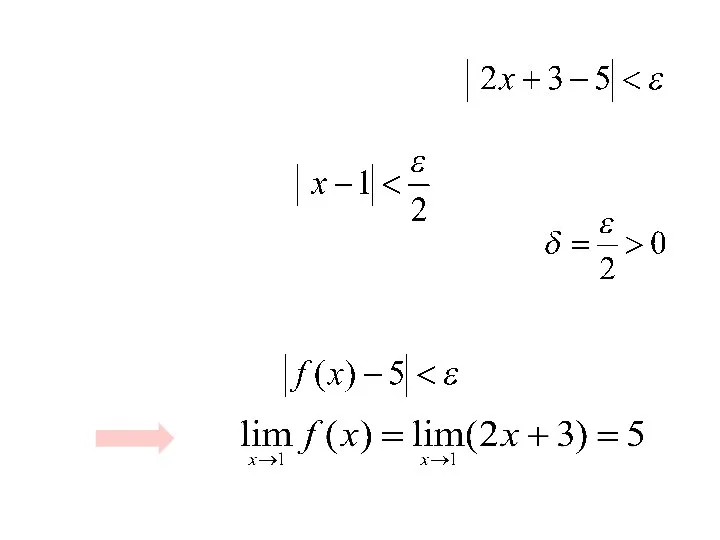


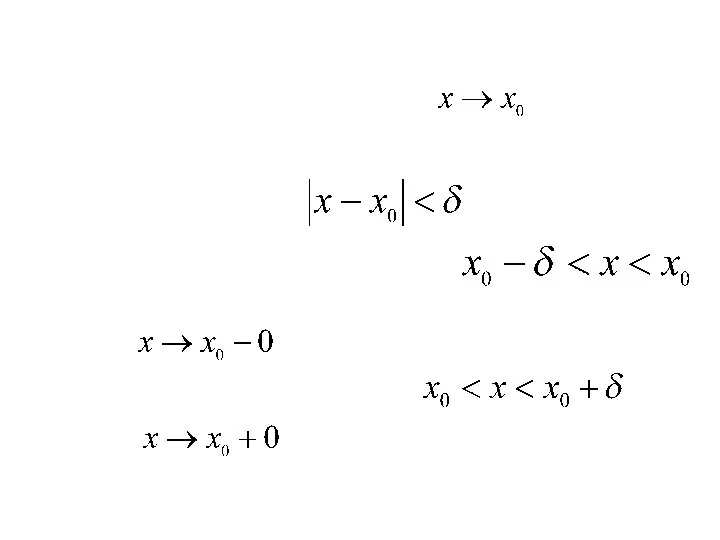
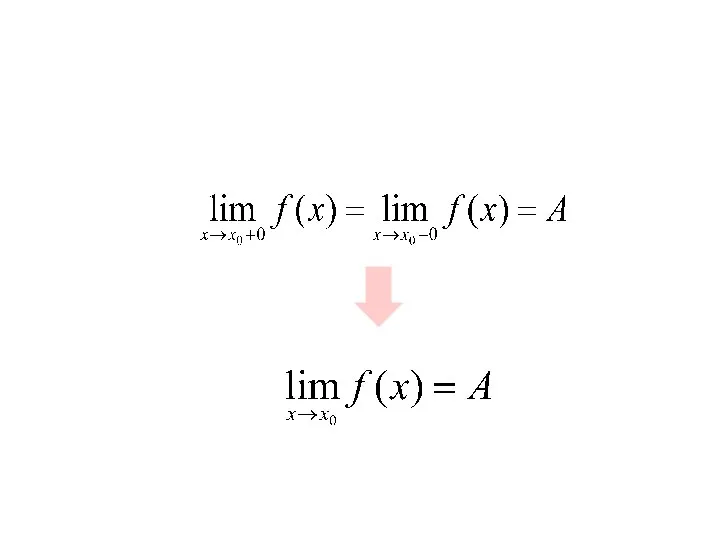









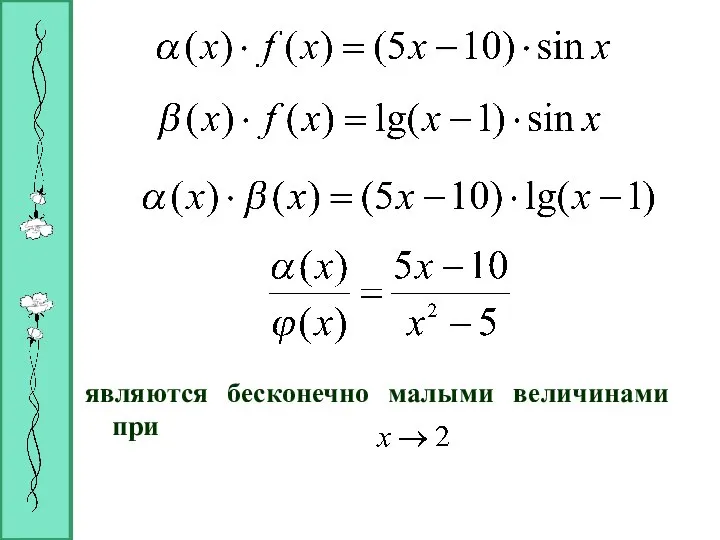
























 Решение заданий
Решение заданий Умножение на двузначные и трёхзначные числа
Умножение на двузначные и трёхзначные числа Влияние коэффициентов квадратного трехчлена на расположение параболы
Влияние коэффициентов квадратного трехчлена на расположение параболы Теорія множин. Відношення
Теорія множин. Відношення Диаграммы. Виды диаграмм
Диаграммы. Виды диаграмм Статические характеристики: среднее арифмтическое
Статические характеристики: среднее арифмтическое Домашнее задание . Подготовка к контрольной работе
Домашнее задание . Подготовка к контрольной работе Математика.Задачки. (тест)
Математика.Задачки. (тест) Куб. Теорема Эйлера
Куб. Теорема Эйлера Подготовка к ОГЭ по математике
Подготовка к ОГЭ по математике Признаки равенства треугольников. Тест
Признаки равенства треугольников. Тест Аттестационная работа. Методическая разработка урока Единицы площади. Квадратный метр. 3 класс
Аттестационная работа. Методическая разработка урока Единицы площади. Квадратный метр. 3 класс Применение свойств арифметических действий сложения и вычитания для рационализации вычисления
Применение свойств арифметических действий сложения и вычитания для рационализации вычисления Определение медианы
Определение медианы Целое уравнение и его корни
Целое уравнение и его корни Основные комбинаторные конфигурации
Основные комбинаторные конфигурации Основные понятия теории вероятностей. Классическое определение вероятности и ее свойства. Правила
Основные понятия теории вероятностей. Классическое определение вероятности и ее свойства. Правила Арифметическая прогрессия
Арифметическая прогрессия Неравенства. Проверь примеры
Неравенства. Проверь примеры Расстояние между двумя точками. 9 класс
Расстояние между двумя точками. 9 класс Понятие. Отношения между понятиями
Понятие. Отношения между понятиями Математический диктант
Математический диктант Нулевая гипотеза
Нулевая гипотеза Таблица сложения
Таблица сложения Алгебраические выражения
Алгебраические выражения Объем куба. Задача
Объем куба. Задача Построение сечений
Построение сечений Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3
Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3