Построение сечений. Задачи

Определение
Секущей плоскостью тетраэдра (или параллелепипеда) называется любая плоскость, по обе стороны от которой имеются точки данного тетраэдра (параллелепипеда).
Многоугольник, который будет образован этими отрезками, называется сечением тетраэдра (параллелепипеда).

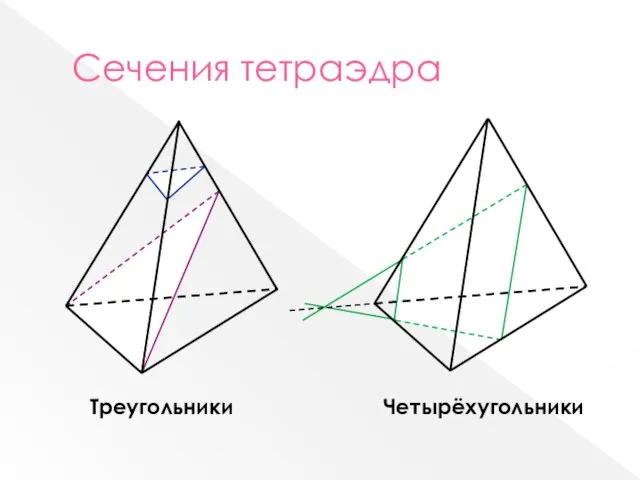
Сечения тетраэдра
Треугольники
Четырёхугольники

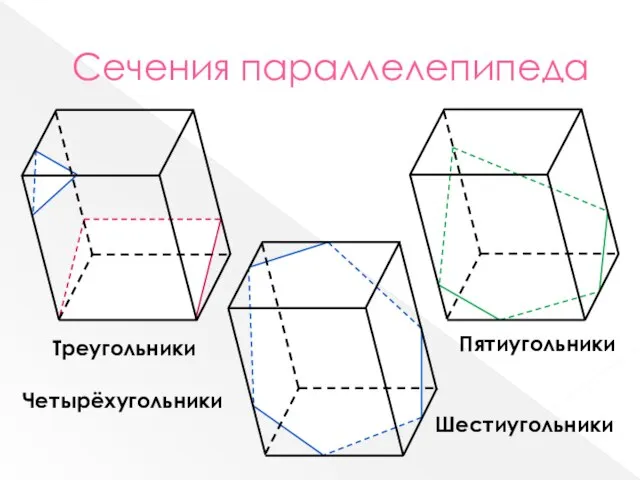
Сечения параллелепипеда
Треугольники
Четырёхугольники
Пятиугольники
Шестиугольники

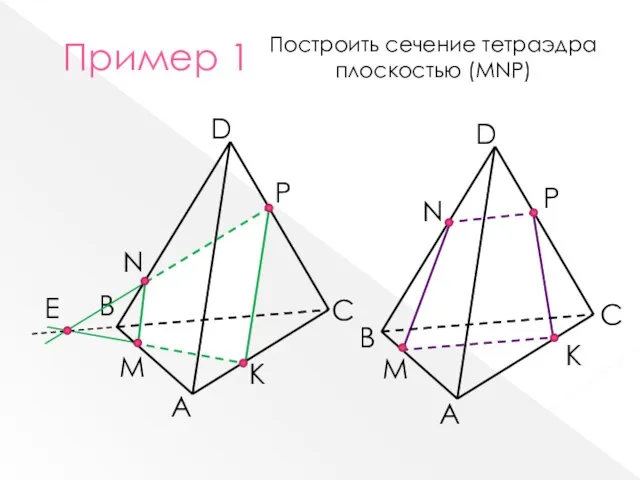
B
Пример 1
A
C
D
M
N
Р
Е
К
B
A
C
D
M
N
Р
К
Построить сечение тетраэдра плоскостью (MNP)

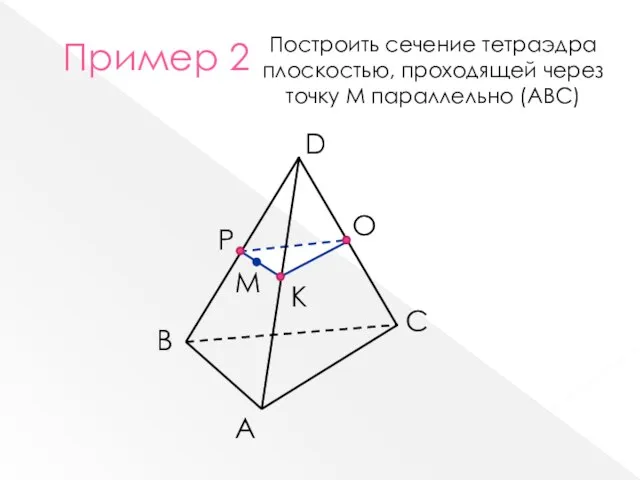
B
A
D
M
С
Р
К
О
Пример 2
Построить сечение тетраэдра плоскостью, проходящей через точку M параллельно (АВС)

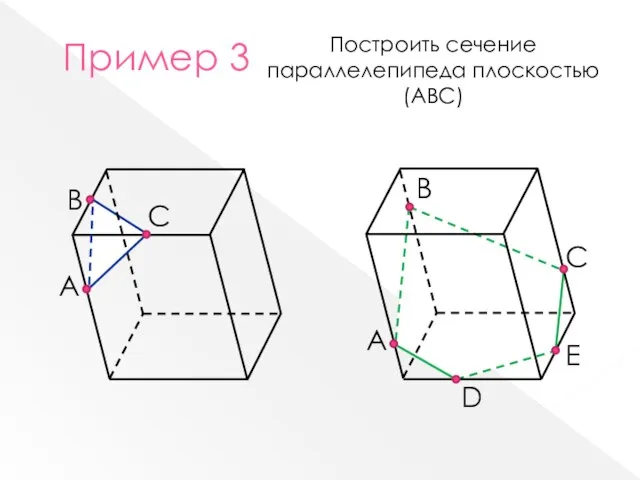
B
A
С
A
B
С
D
E
Пример 3
Построить сечение параллелепипеда плоскостью (АВС)

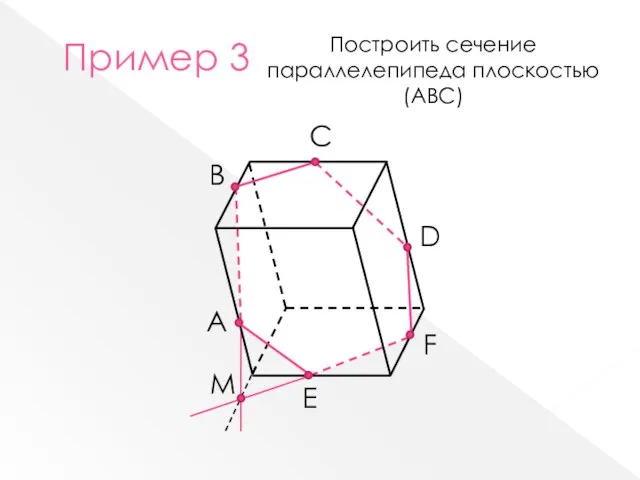
B
A
С
М
E
F
D
Пример 3
Построить сечение параллелепипеда плоскостью (АВС)

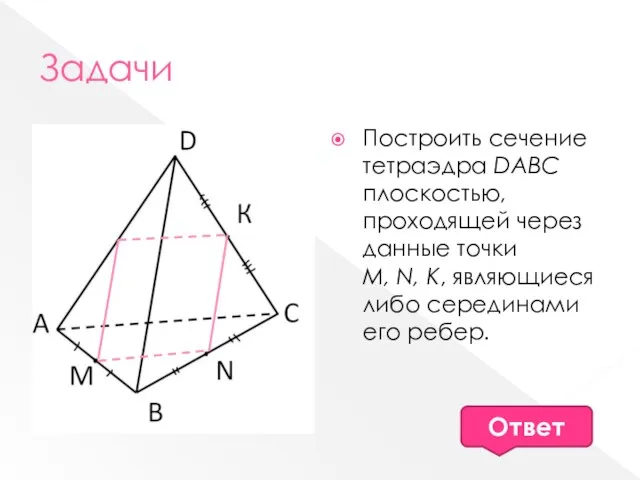
Задачи
Построить сечение тетраэдра DABC плоскостью, проходящей через данные точки
М, N, К, являющиеся либо серединами его ребер.
Ответ

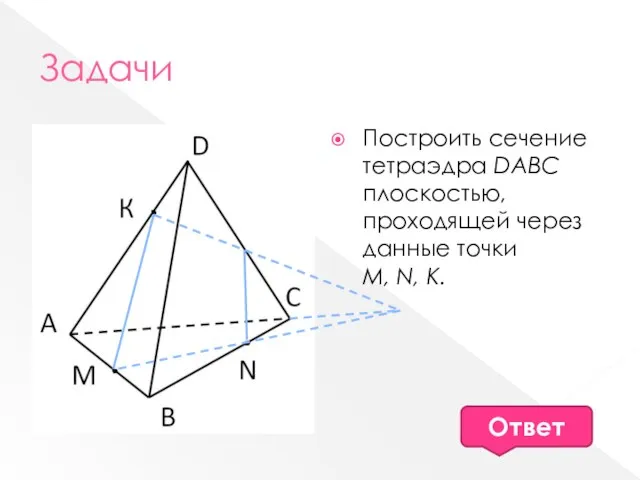
Задачи
Построить сечение тетраэдра DABC плоскостью, проходящей через данные точки
М, N, К.
Ответ